香港大学：Seminar on Applications of Mathematics - Voting

Outline Examples of voting system -What should be an ideal voting system Arrow's Impossibility Theorem Main idea of the proof of Arrow's Impossibility Theorem Yes-no voting systems and the dimension of these systems. How to quantify political power -Examples of power indices and their applications to the LEGCO voting system

Outline ƒ Examples of voting system ƒ What should be an ideal voting system ? ƒ Arrow's Impossibility Theorem ƒ Main idea of the proof of Arrow's Impossibility Theorem ƒ Yes-no voting systems and the dimension of these systems. ƒ How to quantify political power ? ƒ Examples of power indices and their applications to the LEGCO voting system

Simple majority vote for two candidates When there are only two candidates or alternatives,we can simply use the simple majority vote. The situation is much more complicated if we have at least three candidates or alternatives

Simple majority vote for two candidates ƒ When there are only two candidates or alternatives, we can simply use the simple majority vote. ƒ The situation is much more complicated if we have at least three candidates or alternatives

Voting Paradox Suppose we have three candidates,A,B and C,and that there are three voters with preferences as follows: Voter 1:A>B>C Voter 2:B >C>A Voter 3:C >A>B For A vs B,A wins(2 to 1) For B vs C,B wins(2 to 1) For C vs A,C wins(2 to 1) ■ Therefore,the requirement of majority rule then provides no clear winner. This is paradoxical,because it means that majority wishes can be in conflict with each other

Voting Paradox Suppose we have three candidates, A, B and C, and that there are three voters with preferences as follows: Voter 1: A> B> C Voter 2: B >C> A Voter 3: C >A> B „ For A vs B, A wins (2 to 1) „ For B vs C, B wins (2 to 1) „ For C vs A, C wins (2 to 1) „ Therefore, the requirement of majority rule then provides no clear winner. „ This is paradoxical, because it means that majority wishes can be in conflict with each other

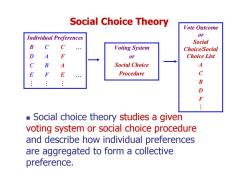
Social Choice Theory Vote Outcome Individual Preferences or Social B C C Voting System Choice/Social D A or Choice List C B A Social Choice A E F E Procedure C B D F Social choice theory studies a given voting system or social choice procedure and describe how individual preferences are aggregated to form a collective preference

M M M E F E … C B A D A F B C C … Individual Preferences Voting System or Social Choice Procedure Vote Outcome or Social Choice/Social Choice List A C B D F M Social Choice Theory „ Social choice theory studies a given voting system or social choice procedure and describe how individual preferences are aggregated to form a collective preference

Who is your favorite hero A C SUPERMAN B E D

Who is your favorite hero ? A B C E D

What is your preference My preference list is B>D>C>A>E How to determine who is the most popular hero?

What is your preference ? „ My preference list is B > D > C > A > E How to determine who is the most popular hero?

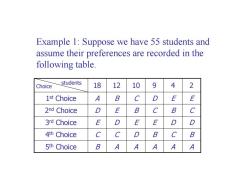
Example 1:Suppose we have 55 students and assume their preferences are recorded in the following table. Choice students 18 12 10 9 4 2 1st Choice A B C D E E 2nd Choice D E B C B 3rd Choice E D E E D 4th Choice C C D B B 5th Choice B A A A A A

A D E B C 10 A B E C D 9 A C D E B 12 2nd Choice D B C 3rd Choice E D D 4th Choice C C B 5th Choice B A A 1 A E E st Choice 18 4 2 students Choice Example 1: Suppose we have 55 students and assume their preferences are recorded in the following table

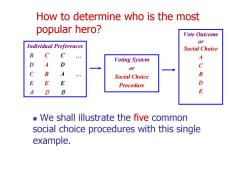
How to determine who is the most popular hero? Vote Outcome or Individual Preferences Social Choice B C C Voting System A D A C or C B A Social Choice B E E E Procedure D A D B E We shall illustrate the five common social choice procedures with this single example

A D B E E E C B A … D A D B C C … Individual Preferences Voting System or Social Choice Procedure Vote Outcome or Social Choice A C B D E „ We shall illustrate the five common social choice procedures with this single example. How to determine who is the most popular hero?

Social Choice Procedure 1: Plurality Voting Plurality voting is the social choice procedure that most directly generalizes the idea of simple majority vote from the easy case of two candidates to the complicated case of three or more candidates. The idea is simply to declare as the social choice(s) the candidate with the largest number of first-place rankings in the individual preference lists

Social Choice Procedure 1: Plurality Voting „ Plurality voting is the social choice procedure that most directly generalizes the idea of simple majority vote from the easy case of two candidates to the complicated case of three or more candidates. „ The idea is simply to declare as the social choice(s) the candidate with the largest number of first-place rankings in the individual preference lists

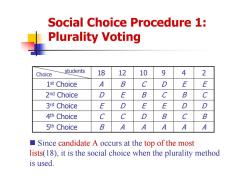
Social Choice Procedure 1: Plurality Voting students Choice 18 12 10 9 4 2 1st Choice A B C D E E 2nd Choice D E B C B 3rd Choice E D E E 4th Choice C C D B B 5th Choice B A A A A A Since candidate A occurs at the top of the most lists(18),it is the social choice when the plurality method is used

Social Choice Procedure 1: Plurality Voting „ Since candidate A occurs at the top of the most lists(18), it is the social choice when the plurality method is used. A D E B C 10 A B E C D 9 A C D E B 12 2nd Choice D B C 3rd Choice E D D 4th Choice C C B 5th Choice B A A 1 A E E st Choice Choice 18 4 2 students