香港大学：Games and the Mathematical Mind

香港大學理學院 Games and the Mathematical Mind Dr.Ng Tuen Wai Department of Mathematics,HKU

Games and the Mathematical Mind Dr. Ng Tuen Wai Department of Mathematics, HKU

What shall we do in this workshop Play some interesting games like HEX. For these games,consider the following questions: .Is it possible for the game to have a draw? .Is it possible for one of the players to have a winning strategy?If it is possible,who should have a winning strategy and what should be a winning strategy? ■ We shall apply Zermelo's Theorem to answer these questions

What shall we do in this workshop ? „ Play some interesting games like HEX. „ For these games, consider the following questions: „ Is it possible for the game to have a draw? „ Is it possible for one of the players to have a winning strategy? If it is possible, who should have a winning strategy and what should be a winning strategy? „ We shall apply Zermelo’s Theorem to answer these questions

What shall we do in this workshop? Learn some problem solving techniques based on the great mathematician George Polya's method (please refer to "How to solve it"). Finally,there will be a group competition on solving some mathematics problems

What shall we do in this workshop? „ Learn some problem solving techniques based on the great mathematician „ Finally, there will be a group competition on solving some mathematics problems. George Pólya ’s method (please refer to “How to solve it”)

HEX You can play Hex with your friends at http://hkumath.hku.hk/~wkc/MathModel/index.php

You can play Hex with your friends at http://hkumath.hku.hk/~wkc/MathModel/index.php

Hex or Nash is a two-player game played on a rhombic board with hexagonal cells. It was invented by a Danish mathematician Piet Hein in 1942,and became popular under the name of Hex

„ Hex or Nash is a two-player game played on a rhombic board with hexagonal cells. „ It was invented by a Danish mathematician Piet Hein in 1942, and became popular under the name of Hex

The game was re-discovered in 1948 by John Nash when he was a phD student at Princeton. At that time,the game was commonly called Nash. NASH 2R(* A Beautiful Mind HAROLD.KUHN 2d SYLVIA NASAR u

The game was re-discovered in 1948 by John Nash, when he was a PhD student at Princeton. At that time, the game was commonly called Nash . A Beautiful Mind

Questions one may ask... -Is it possible to end in a draw -Is there a winning strategy for one of the players

Questions one may ask … „ Is it possible to end in a draw ? „ Is there a winning strategy for one of the players ?

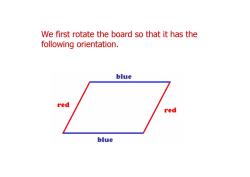
We first rotate the board so that it has the following orientation. blue red red blue

We first rotate the board so that it has the following orientation

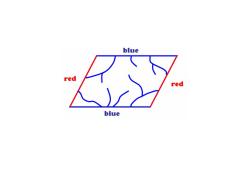
blue red red blue

Further questions -We may then ask the following questions: -Is it possible for one of the players to have a winning strategy? -If it is possible,who should have a winning strategy? What do we mean by a winning strategy Drawing strategy

Further questions „ We may then ask the following questions: „ Is it possible for one of the players to have a winning strategy? „ If it is possible, who should have a winning strategy? „ What do we mean by a winning strategy ? Drawing strategy ?