同济大学:《结构动力学》课程教学资源(教案讲义)Lecture 04 Response to harmonic and periodic excitations - Application

Structural Dynamics Lecture 4 Response to harmonic and periodic excitations: Application 目 同榜大学 上水工程学院 COLLEGE OF CIVIL ENGINEERING
Structural Dynamics Lecture 4 Response to harmonic and periodic excitations: Application

Contents Response of SDOF to harmonic excitation: application Identify the natural frequency and damping ratio Vibration measurements Earthquake Isolation ·Vibration Isolation Response of SDOF to periodic excitation 闺 土本2程学院
Contents Response of SDOF to harmonic excitation: application • Identify the natural frequency and damping ratio • Vibration measurements • Earthquake Isolation • Vibration Isolation Response of SDOF to periodic excitation

Field test of full-scale structures:Vibration shaker Rotating machine with eccentric mass p(1)=(meo)sin(ot) m。:maSS e:eccentricity @rotating frequency 35 kg vibration shaker Max.Force generated1500T 闺 土本程李悦
35 kg vibration shaker Max. Force generated1500T Field test of full-scale structures: Vibration shaker • Rotating machine with eccentric mass 2 sin e p t m e t : : : m mass e e eccentricity rotating frequency
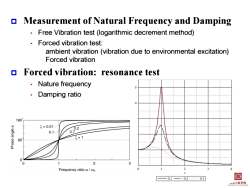
Measurement of Natural Frequency and Damping Free Vibration test(logarithmic decrement method) Forced vibration test: ambient vibration(vibration due to environmental excitation) Forced vibration Forced vibration:resonance test Nature frequency Damping ratio 180 g=0.01 0.1 002 90 5=1 Frequency ratio/n —0.1-02…0.5 目 二水二程季院
Measurement of Natural Frequency and Damping • Free Vibration test (logarithmic decrement method) • Forced vibration test: ambient vibration (vibration due to environmental excitation) Forced vibration Forced vibration: resonance test • Nature frequency • Damping ratio
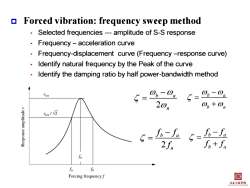
Forced vibration:frequency sweep method Selected frequencies---amplitude of S-S response Frequency-acceleration curve Frequency-displacement curve(Frequency -response curve) Identify natural frequency by the Peak of the curve Identify the damping ratio by half power-bandwidth method 5-0。-0 5=0-02 20n 0b+0a es/W② 6=f上5-人- 2f f6+f。 fa 6 Forcing frequencyf 闺 土亦工鞋季悦
Forced vibration: frequency sweep method • Selected frequencies --- amplitude of S-S response • Frequency – acceleration curve • Frequency-displacement curve (Frequency –response curve) • Identify natural frequency by the Peak of the curve • Identify the damping ratio by half power-bandwidth method 2 b a n b a b a 2 b a n f f f b a b a f f f f

Equivalent viscous damping f+fD+f=f。 ∫fid+∫fn+jrau=Sfchu Conclusion:In steady state response,the energy input to the system due to the applied force is dissipated in viscous damping 目 主求2相季院
Equivalent viscous damping • Conclusion: In steady state response, the energy input to the system due to the applied force is dissipated in viscous damping I D s p f f f f I D s p f du f du f du f du

Energy dissipated in viscous damping in each vibration cycle. E=[Iodu-"(cu)idt=eu'dr 2π10 2π10 =c[ou,cos(ot-)di =πC0uo =25 ku Energy dissipated in viscous damping is proportional to the square of motion amplitude,and damping ratio and w 土本工相季汽
• Energy dissipated in viscous damping in each vibration cycle. 2 / 2 / 2 0 0 2 / 2 0 0 2 0 2 0 cos 2 D D n E f du cu udt cu dt c u t dt c u ku • Energy dissipated in viscous damping is proportional to the square of motion amplitude, and damping ratio and w

In steady state response,the energy input to the system due to the applied force is dissipated in viscous damping E,=Sp()du=p(t)idr (po sin )[ou cos(di sm28风-28) uo Po/k 目 土本之相学院
• In steady state response, the energy input to the system due to the applied force is dissipated in viscous damping 2 / 0 2 / 0 0 0 2 0 0 0 sin cos sin 2 I n E p t du p t udt p t u t dt p u ku 0 0 sin 2 2 / d n n u R p k

Potential energy by spring element Es =Jfdu=(kut)idr k[u sin(t)]Lou cos(t-)]dt=0 Energy by inertia force Ex -fdu-(miyidr -m[-oiusin(t-)][ou cos(-)]di=0 2π/0 目 土本程李悦
• Potential energy by spring element 2 / 0 2 / 0 0 0 sin cos 0 E f du ku udt S s k u t u t dt • Energy by inertia force 2 / 0 2 / 2 0 0 0 sin cos 0 E f du mu udt K I m u t u t dt
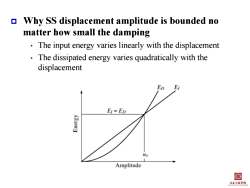
Why SS displacement amplitude is bounded no matter how small the damping The input energy varies linearly with the displacement The dissipated energy varies quadratically with the displacement Ep E EI=ED Amplitude 目 主京2相季院
Why SS displacement amplitude is bounded no matter how small the damping • The input energy varies linearly with the displacement • The dissipated energy varies quadratically with the displacement
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 同济大学:《结构动力学》课程教学资源(教案讲义)Lecture 03 Response to Harmonic and Periodic Excitations.pdf
- 同济大学:《结构动力学》课程教学资源(教案讲义)Lecture 02.pdf
- 同济大学:《结构动力学》课程教学资源(教案讲义)Lecture 01 Introduction of Structural Dynamics(负责人:陈隽).pdf
- 《力学》课程教学资源(试卷习题)美国物理试题与解答(第1卷)力学.pdf
- 长沙理工大学:《力学》课程教学资源(大纲教案)教学大纲 Mechanics.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)专题部分——机械振动基础.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第十四章 虚位移原理 §14-1 约束、虚位移、虚功 §14-2 虚位移原理(虚功原理).pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第十三章 达朗贝尔原理.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第十二章 动能定理 §12-6 普通定理的综合应用举例..pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第十二章 动能定理 §12-1 力的功 §12-2 质点和质点系的功能 §12-3 动能定理.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第十一章 动量矩定理 §11-3 刚体绕定轴的转动微分方程 §11-5 质点系相对质心的动量矩定理 §11-6 刚体的平面运动微分方程.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第十一章 动量矩定理 §11-1 质点和质点系的动量矩 §11-2 动量矩定理 §11-4 刚体对轴的转动惯量.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第十章 动量定理 §10-3 质心运动定理.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第九章 质点动力学的基本方程、第十章 动量定理 §10-1 动量与冲量 §10-2 动量定理.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第八章 刚体的平面运动 §8-5 运动学综合应用举例.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第八章 刚体的平面运动 §8-4 用基点法求平面图形内各点的加速度.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第八章 刚体的平面运动 §8-1 刚体平面运动的概述和运动分解 §8-2 求平面图形内各点速度的基点法 §8-3 求平面图形内各点速度的瞬心法.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第七章 点的合成运动(复合运动)§7-4 牵连运动为转动时点的加速度合成定理·科氏加速度.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第七章 点的合成运动(复合运动)§7-3 牵连运动为平移时点的加速度合成定理.pdf
- 北京化工大学:《理论力学》课程教学资源(教案讲义)第七章 点的合成运动(复合运动)§7-1 相对运动,牵连运动,绝对运动 §7-2 点的速度合成定理.pdf
- 同济大学:《结构动力学》课程教学资源(教案讲义)Lecture 05 Response to Arbitrary, Step , and Pulse Excitations.pdf
- 同济大学:《结构动力学》课程教学资源(教案讲义)Lecture 06 Numerical Evaluation of Dynamic Response.pdf
- 同济大学:《结构动力学》课程教学资源(教案讲义)Lecture 07 Frequency Domain Method.pdf
- 同济大学:《结构动力学》课程教学资源(教案讲义)Lecture 08 Generalized SDOF Systems.pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)01 Introduction.pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)02 Kinematic(运动学)analysis of structures.pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)03 Reactions(反力).pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)04 Member Forces in Planar Trusses平面桥架()and Space Frameworks(空间构架).pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)05 Member Forces in Beams(梁)and Frames.pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)07 Elastic Deflections(弹性变形)of Trusses and Frameworks..pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)08 Elastic Deflections(弹性变形)of Beam and Frame Structures.pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)09 More Basic Concepts of Structural Analysis.pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)06 Influence Lines(影响线)and Maximum Load Effects..pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)10 Method of Consistent Deformations(协调变形法)(and Other Compatibility Methods).pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)11 Slope Deflection Method(转角变位移法)(and Other Equilibrium Methods).pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)12 Moment Distribution Method(弯矩分配法).pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)13 Matrix Displacement Method(矩阵位移法).pdf
- 同济大学:《结构力学》课程教学资源(教案讲稿,打印版)16 Dynamic analysis of structures.pdf
- 吉林大学:《土质学与土力学》课程教学资源(讲义,共十一章,负责人:郑孝玉).docx
- 科学出版社:现代力学丛书《高等断裂力学》书籍PDF电子版 Advanced Fracture Mechanics(2009版,共14章,主编:王自强、陈少华).pdf
