同济大学：《结构力学》课程教学资源（教案讲稿，打印版）11 Slope Deflection Method（转角变位移法）（and Other Equilibrium Methods）

Chapter 11. Slope Deflection Method(转角变位移法) (and Other Equilibrium Methods). 月大学 自 土工程学院 TONGJI UNIERSITY 11.1 Nature of equilibrium methods Equilibrium The fundamental equations are methods the equations of equilibr Compatibility (平衡法) method（协调 法) Stiffness The fundamental equations are method (刚度法) composed of stiffness q Flexibility method（柔度 法) Displaceme The solution of the fund aa nt method (位移法) equations are displacemente Force method( 力法) 月大学 土木工程学院 TONGUNIVERSITY

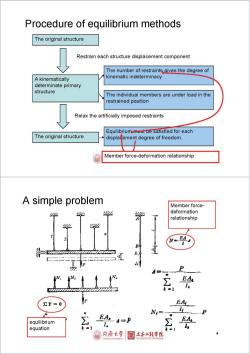
Procedure of equilibrium methods The original structure Restrain each structure displacement component The number of restraints qives the degree of A kinematically kinematic indeterminacy determinate primary structure The individual members are under load in the restrained position Relax the artificially imposed restraints Equilibrium must be satisfied for each The original structure displadement degree of freedom. Member force-deformation relationship A simple problem Member force- deformation relationship N=EAA B P EA Y=0 EA N,= equilibrium xd=P EAx equation L 冠月海大学 土床工程学院

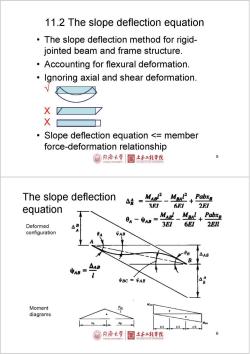
11.2 The slope deflection equation The slope deflection method for rigid- jointed beam and frame structure. Accounting for flexural deformation. Ignoring axial and shear deformation. X X Slope deflection equation <member force-deformation relationship @同傍大学目土本红程幸院 The slope deflection △8 MABl2 MRAP2 Pabxp equation 3EI 6EI 0A-中AB= MAnl MaAl Pabxe Deformed 3E1 6EI 2EIl configuration y 中AB BC VAB Moment diagrams /3 3 1/3 同僑大学 土本工程学院 6

The slope 0-AB= MAR!MRAL Pabxg deflection 3E1 6EI 2EIl M过+M然 Pabx equation 6EI 3EI 2Ell continued The slope deflection equation MA8-Member-end moment 2E1 MAB (20+0-3)+FEMAm FEMAB-Fixed-end moment M2)FEM n-near end M=2EK(20+-3+FEM f-far end Krstiffness factor 4EI。,2E 。6E1 Knr=//,unit stiffness; Mg8+ 0- 24 stiffness per unit length; 线刚度 以份不子闺人 Fixed-end moments(固端弯矩) Loading MAB MBA -Pab2 +Pa2b -w2 +w2 12 2 +w2 20 晋-+) +b(2a-b) M +ab-告 国二

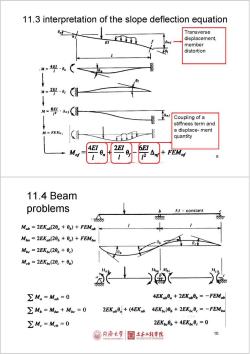
11.3 interpretation of the slope deflection equation Transverse displacement, member distortion M=4·9， M=24.9 /2 Coupling of a stiffness term and a displace-ment quantity 4EI FEMnf 9 11.4 Beam problems b /constant Mab 2EKab(20 +0p)+FEMab Mba 2EKab(20p+0a)+FEMba Mbc 2EKbe(20p+0c) Mcb=2EKc(20。+0b) ∑M。=Mb=0 4EKab0 2EKab0=-FEMab ∑M6=Mba+Mbc=0 2EKab0.+(4EKab4EKbc)8。+2EK0。=-FEMbo ∑Me=Mcb=0 2EKbe0。+4EKe0。=0 同榜大学 土床工程学院 10

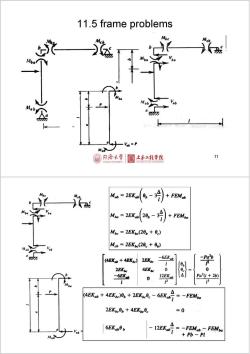
11.5 frame problems 一V= 同停大学 目 土床工程学院 11 FEMab Mba 2EKab 20。-3号》 FEM Mc=2EKbc(20。+0.) Meb 2EKbe(20c+0g) (EK+4EKc) 2EKpe -6EKab -Pa2b 2EKbe 4EKbc 0 0 -6EK业 0 12EKab Pa"(l 2b) 2 下 4EK+EK)+2EK-EK =-FEMbe 2EK0+4EKbc0c =0 6EKab0 -12EKab =-FEMab FEMba Ma Pb-Pl

Procedure of the slope deflection method The displacement boundary conditions A qualitative sketch of the deflected structure The compatibility requirements The unknown displacement quantities A slope deflection equation for each member end A rotational freedom involving the An equilibrium equation for moments acting on the joint each kinematic dof A sway freedom involving column shears and moments The equilibrium equations in terms of unknown displ. Determination of the unknown displacements End moments coming from the slope deflection equation 同榜大学 土本工程学院 13 Example 11.2 Determine the end moments and the maximum bending stress for the structure below,if point b settles 0.03m. E=200×10Pa=200GN/m2:1=2000×10-6m:d=0.3 m(beam depth) 0.03m b ab=0.03/10=0.003 c=-0.003 Compatibility and Boundary Conditions 0 and 0 are the two kinematic degrees of freedom. Moment Equations M=2EK(20+0-3)+FEM Kb=K=K=200X10-6m=200×10-7m 10m EK=200GN× m×200×107m3=40MN.m 14

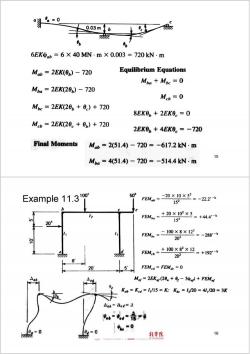
议 =0 0.03m 6EKψab=6×40MN.m×0.003=720kN.m Mb=2EK(0b)-720 Equilibrium Equations Mba Mic =0 Mba=2EK(20b)-720 Mcb=0 Mbc=2EK(20b+0)+720 8EK0b+2EK0。=0 Mb=2EK(20。+0b)+720 2EK0。+4EK0.=-720 Final Moments Mb=2(51.4)-720=-617.2kN·m 15 Ma=451.4)-720=-514.4kN.m Example 11.310 50 FEMb=-20X10×52 =-22.2'-k 152 FEM=+20X02×5-+444-t n 20 152 FBM=二10X8X12=-288-+ 202 FEMb=+10×82X2=+192-k 202 81 5 FEMed=FEMdc=0 My=2EKy (20+0-3+FEM Kab=Kod =1/15=K;Kic 12/20=41 120=3K △ab=4cd=4 u或6=音产号 鼎0 90 吃e=0 程学脱 16

100 50 Me=-(50×5)=-250'-k (from statics) Mab=2EK(0。-3)-22.2 20 Ma=2EK(20。-3)+44.4 M=2E·3K(20b+0)-288 汤 n 8 20 5 Mb=2E·3K(20e+6b)+192 Mcd=2EK(20。-3ψ) Equilibrium Equations Mk=2EK(0e-3ψ) At joint b: Msa Moc =0 250h At joint c: M+M-250=0 学院 17 Columns ab and cd: 5 204 10 一H Mab M from consideration of the entire structure, H。+Ha=20 .'.Mab Mpe Mca+Mac =-200 Substitution of moment equations into the equilibrium equations yields 6 -61EK06l [243.6 6 16 EKO。 58.0 -6 24 EK业 222.2 18

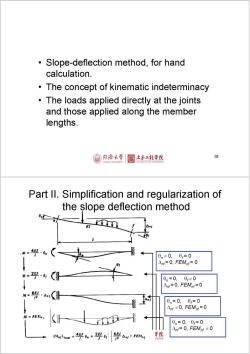
Slope-deflection method,for hand calculation. The concept of kinematic indeterminacy The loads applied directly at the joints and those applied along the member lengths. 同橋大学 土水工相学院 19 Part ll.Simplification and regularization of the slope deflection method EI 0n≠0， 0=0 △r=0,FEMpt?=0 .M=- 0n=0,0r≠0 △t=0,FEMf=0 6 6n=0,0=0 △nr≠0，FEMot=0 M=FEn】 0n=0,0,=0 △nf=0,FEMnt≠0 nl1ow=4号n+2g财2a1+FEMn 学院