同济大学：《结构力学》课程教学资源（教案讲稿，打印版）12 Moment Distribution Method（弯矩分配法）

2016/4/6 Chapter 12 Moment Distribution Method(弯矩分配法) 输问冷大学 国土本2程学院 Background Methods for statically indeterminate structures:(超静定结构的计算方法) ·Force method(力法) ·Displacement method(位移法) ·Moment distribution method(弯矩分配法) 司问冷大学 闺土本红相季院 1

2016/4/6 1 1 Chapter 12 Moment Distribution Method（弯矩分配法） Background Methods for statically indeterminate structures:（超静定结构的计算方法） • Force method （力法） • Displacement method （位移法） • Moment distribution method（弯矩分配法）

2016/4/6 16 Candy distribution Game! 4 6 6 5 6 xWhat is the basic idea? 输问济大学 国土本2程季悦 Key points of distribution method 1.It does not need a complete set of equations. Force method A,=∑δyX,+AP Displacement method R-25Z,+R=0 2.It is a step-by-step iterative(送代)method. 3.Each step acts to refine the result from the previous step. 4.The process converges (to the correct solution with enough steps. 5.The process can be terminated(终止)when the desired accuracy(精度)has been achieved 包同冷大学 闺土本红程学院 2

2016/4/6 2 3*y=16 y=? Candy distribution What is the basic idea? 16 0 8 8 4 4 8 4 6 6 5 5 6 Game! 3. Each step acts to refine the result from the previous step. 4. The process converges (收敛) to the correct solution with enough steps. 5. The process can be terminated (终止) when the desired accuracy (精度) has been achieved. Key points of distribution method 2. It is a step-by-step iterative (迭代) method. 1. It does not need a complete set of equations. Force method Displacement method P 0 1     i n j Ri rijZ j R P 1 i n j i ijX j   

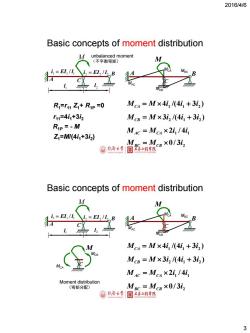
2016/4/6 Basic concepts of moment distribution M unbalanced moment (不平衡弯矩) i2=E2/12 B R=r11Z+RiP=0 Mc4=M×4i1/(4i1+3i2) r11=411+3i2 McB=M×3i2/(4i1+3i2) Rip =-M MAc=Mc4×2i1/4i1 Z1=M川4i1+3i2) MaC=McB×0/3i2 输问济大学 士齐1程幸悦 Basic concepts of moment distribution M i,=E1,/l A M Mc4=M×4i/(4i,+3i2) McB McB=M×3i2/(4i+3i2) McA n M4c=Mc4×2i,/4i1 Moment distribution (弯矩分配) MBc=McB×0/3i2 包同冷大学 国产本红相学院 3

2016/4/6 3 A B C M MCA MCB MBC MAC M A B 1 l 2 l 1 1 1 i  EI / l 2 2 2 i  EI / l C 4 /(4 3 ) 1 1 2 M M i i i CA    3 /(4 3 ) 2 1 2 M M i i i CB    1 4 1 M M 2i / i AC  CA  3 2 M M 0/ i BC  CB  Basic concepts of moment distribution R1=r11 Z1+ R1P =0 r11=4i1+3i2 Z1=M/(4i1+3i2 ) R1P = - M unbalanced moment （不平衡弯矩） A B C M MCA MCB MBC MAC M A B 1 l 2 l 1 1 1 i  EI / l 2 2 2 i  EI / l C 4 /(4 3 ) 1 1 2 M M i i i CA    3 /(4 3 ) 2 1 2 M M i i i CB    M M C CA MCB 1 4 1 M M 2i / i AC  CA  3 2 M M 0/ i BC  CB  Moment distribution （弯矩分配） Basic concepts of moment distribution

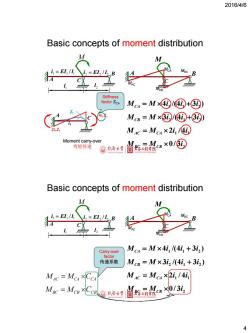
2016/4/6 Basic concepts of moment distribution Stiffness factor ScA Mc4=M×④/④+③@) 4i2 Ms=M×⑤/④+3①) MAc=Mc4×2i,/① Moment carry-over 弯矩传递 M Mcs×0/② 织程流 Basic concepts of moment distribution M =E11 2=E12/2B 公A Carry-over Mc4=M×4i/(4i1+3i2) factor 传递系数 MB=M×3i2/(4i+3i2) Mac McxCea MAc=McA×2i,/4i Mc=MCB XCCB③月卡 4cs0/3列 4

2016/4/6 4 A B C M MCA MCB MBC MAC M A B 1 l 2 l 1 1 1 i  EI / l 2 2 2 i  EI / l C 4 /(4 3 ) 1 1 2 M M i i i CA    3 /(4 3 ) 2 1 2 M M i i i CB    1 4 1 M M 2i / i AC  CA  3 2 M M 0/ i BC  CB  Basic concepts of moment distribution A C Moment carry-over 弯矩传递 4i1Z1 2i1Z1 Z1 i1 Stiffness factor SCA A B C M MCA MCB MBC MAC M A B 1 l 2 l 1 1 1 i  EI / l 2 2 2 i  EI / l C 4 /(4 3 ) 1 1 2 M M i i i CA    3 /(4 3 ) 2 1 2 M M i i i CB    1 4 1 M M 2i / i AC  CA  3 2 M M 0/ i BC  CB  Basic concepts of moment distribution M M C AC CA CA   M M C BC CB CB   Carry-over factor 传递系数

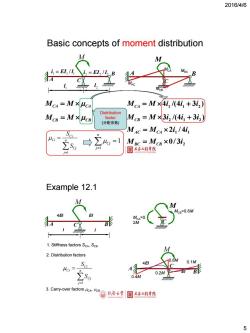
2016/4/6 Basic concepts of moment distribution M i=EI2/1 B Mc MXHc Mc4=M×41,/4i1+3i2) Distribution MCB MXHCB factor McB=M×3i2/(4i,+3i2) (分配系数) MAc=Mc4×2i,/4i1 Mac=McB×0/3i2 Example 12.1 M McB=0.8M 4E MCA 2M 1.Stiffness factors ScA.ScB 2.Distribution factors Sa 0.1M Sg 0.2M 0.4M j 3.Carry-over factors McA.AcB 圆间冷大学 目土本江相幸院 5

2016/4/6 5 A B C M MCA MCB MBC MAC M A B 1 l 2 l 1 1 1 i  EI / l 2 2 2 i  EI / l C 4 /(4 3 ) 1 1 2 M M i i i CA    3 /(4 3 ) 2 1 2 M M i i i CB    1 4 1 M M 2i / i AC  CA  3 2 M M 0/ i BC  CB  Basic concepts of moment distribution MCA  M   CA MCB  M   CB Distribution factor (分配系数) 1 Ci Ci n Cj j S S     1 1 n Cj j     Example 12.1 0.8M 0.2M M C MCA=0. 2M MCB=0.8M 0.1M 0.4M A B C M 4EI EI M A C B l l 4EI EI 1 Ci Ci n Cj j S S     1. Stiffness factors SCA, SCB 2. Distribution factors 3. Carry-over factors CA, CB

2016/4/6 Example 12.2 Take E/and /as constants. 16 n 输月冷大学 目土本2程学税 16 Candy distribution:review Gamel 0 8 8 4 6 5 5 6 包同冷大学 目土本2程幸悦 6

2016/4/6 6 Example 12.2 A B C 16 D Take EI and l as constants. 3*y=16 y=? Candy distribution: review 16 0 8 8 4 4 8 4 6 6 5 5 6 Game!

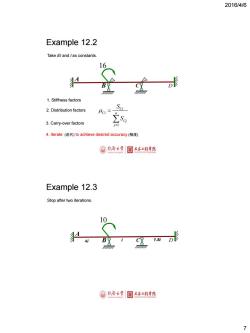
2016/4/6 Example 12.2 Take E/and /as constants. 16 1.Stiffness factors 2.Distribution factors 3.Carry-over factors i=1 4.Iterate(迭代)to achieve desired accuracy(精度) 月冷大学 国土本2程季悦 Example 12.3 Stop after two iterations. 10 41 1.5i D形 国月冷大学 目土本2程幸院 >

2016/4/6 7 Example 12.2 A B C 16 D Take EI and l as constants. 1 Ci Ci n Cj j S S     1. Stiffness factors 2. Distribution factors 3. Carry-over factors 4. Iterate (迭代) to achieve desired accuracy (精度) Example 12.3 A B C 10 4i i 1.5i D Stop after two iterations

2016/4/6 Unbalanced moment due to in-span loading (跨间荷载导致的不平衡弯矩) The negative value of total fixed end moments at the joint is to be distributed. P2 MR+M女9a品 Mc4=M×44+Ma McB=M×4B+MEB MAc MX Hc xCc+Mic MBc M X HcB XCcB+MBc CB 输问冷大学 国土本2相学悦 Factors for different boundary conditions: (不同边界条件下的系数取值) Stiffness factors SAj SAB=4i SAn=3i A B i B Distribution factors MAj ΣS i=1 A Carry-over factors CAj AB=1/2 AB =0 AB A 包向傍大学 目土本工程学院 8

2016/4/6 8 F MCA  M   CA  MCA F MCB  M   CB  MCB R1P C F MCB F MCA ( ) 1 F F M  R P   MCA  MCB Z1 1 A B 1i 2 C i 1 4i 2 3i 1 2i A B 1 l 2 l 1 1 1 i  EI / l 2 2 2 C i  EI / l FP1 FP2 F MAC  M   CA CCA  MAC F MBC  M   CB CCB  MBC Unbalanced moment due to in-span loading （跨间荷载导致的不平衡弯矩） R1P C M The negative value of total fixed end moments at the joint is to be distributed. Factors for different boundary conditions: （不同边界条件下的系数取值） A B S i AB  4 i A B S i AB  3 i A B S i AB  i Distribution factors Aj Carry-over factors CAj    n j Aj Ai Ai S S 1  A B CAB  1/ 2 i A B CAB  0 i A B CAB  1 i Stiffness factors SAj

2016/4/6 Example 12.4 E/=constant,/=6 m,1=5 m. 2.5F 1.5F 1.5F i,=EI/5 Solution: 4B4=0.625,4Bc=0.375。 4cB=0.5,4cD=0.5.4oc=0.706,4oE=0.294。 @月冷大学国产本红指核 B D 0-50.62503750.505050.5070G0294-E￥，F -1.5 2.5 -2.5 -0.469 -0.938-0.562 0.8831.7650.735-0.735 0.281 -0.301-0.301 -0.15 -0.151 0.029 0.0940.0570.0280.0540.1070.044-0.044 -1.94 0.656 -0.65G0.040.041.721.721-3.279 -0.5950.595 41/2 Fp 1.94 1.721 0.656 M(xF) C D i1≥E3 Qi,=E750.595, 3.279 国月冷大学 目土本红相学院 9

2016/4/6 9 Example 12.4 EI=constant，l1=6 m,l2=5 m. A B 1 l 2 l i1  EI / 3 i2  EI / 5 C 2FP FP D E 2 l 1 l 2 i 1 i l1 / 2 5 P 1. F 5 P 2. F 5 P 2. F 5 P 1. F  BA  0.625, BC  0.375。  CB  0.5, CD  0.5。 DC  0.706, DE  0.294。 Solution: A B 0.5 C D 0.6250.375 0.5 0.5 0.5 0.5 0.7060.294 1 E  0.469 0.883  0.735  0.281  0.938  0.562 1.765 0.735  0.301  0.301  0.151  0.151 0.029 0.094 0.057 0.028 0.054 0.107 0.044  0.044 0.656  0.041 0.041  0.656 1.94 1.7211.721  3.279  0.595 0.595 A B 1 l 2 l i1  EI / 3 i2  EI / 5 C 2FP FP D E 2 l 1 l 2 i 1 i l1 / 2 3.279 1.721 0.595 1.94 0.656 ( ) M FP 1.5 1.5  2.5  2.5 ( ) FP

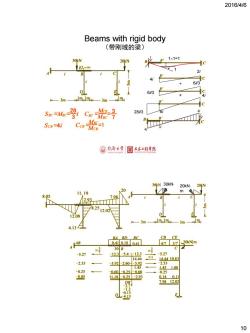
2016/4/6 Beams with rigid body (带刚域的梁) 30kN 1×1=1 20kN El1=∞ 6i/3 63 Swc -Ma MCB_3 283 ScB=4i MBC=1 CCB-MCB @月冷大学 主本1程季院 30kN 30kN. 20kN- 20kN 20 11.18 m 8.05 7.98 2.93 8.25 12.02 12.08 3m 3m 4.13 BA BD BC CB CE 天 0.410.18041 4737 _20kN]m 30B C -5.27 -12.3 -5.41-12.3 -5.27 14.44 ×1 14.4410.83 -2.53 -592 -2.60-5.92 -2.53 1.45 145 108 -0.25 0.60 -0250.6① -0.25 -80 11.18-8.25 -2.93 014 0.11 DB 29812.02 0.13 4.13 10

2016/4/6 10 Beams with rigid body （带刚域的梁） + = 11=1 1 4i 2i 6i/3 6i/3 6i 4i 28i/3 30kN m 20kN m