《土力学与地基基础》课程教学课件（PPT讲稿）第七章 土坡稳定分析 第三节 粘性土坡的稳定分析

第三节粘性土坡的稳定分析粘性土土坡不会沿边坡表面滑动，而是深入士体内滑动。在工程设计中常假定滑动面为圆弧面。建立在这一假定上的稳定分析方法称为圆弧滑动法，它是极限平衡法的一种常用分析方法。1

1 第三节 粘性土坡的稳定分析 ◼ 粘性土土坡不会沿边坡表面滑动，而是 深入土体内滑动。在工程设计中常假定 滑动面为圆弧面。建立在这一假定上的 稳定分析方法称为圆弧滑动法，它是极 限平衡法的一种常用分析方法

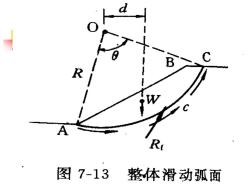
、整体圆弧滑动法（瑞典圆弧法）■设一个均质粘性土坡（图7一13）。假定边坡失去稳定就是滑动土体绕圆心发生转动，把滑动土体当成一个刚体。滑动土体的重量W将使土体绕圆心O旋转，转动力矩为M=Wd，d为过滑动土体重心的竖直线与圆心O的水平距离

2 一、整体圆弧滑动法（瑞典圆弧法） ◼ 设一个均质粘性土坡（图7－13）。假定 边坡失去稳定就是滑动土体绕圆心发生 转动，把滑动土体当成一个刚体。滑动 土体的重量W将使土体绕圆心O旋转，转 动力矩为Ms=Wd，d为过滑动土体重心的 竖直线与圆心O的水平距离

C.BKWARr图7-13整体滑动弧面

3

抗滑力矩M.由两部分组成：一是滑动面AC上粘聚力产生的抗滑力矩，其值为c·AC·R，c为土的粘聚力；另一项是滑动土体重量在滑动面上的反力所产生的抗滑力矩。当土体的内摩擦角Φ=0时，滑动面是一个光滑面，通过圆心○，不产生力矩，因此抗滑力矩只有c·AC·R一项

4 ◼ 抗滑力矩MR由两部分组成：一是滑动面 AC上粘聚力产生的抗滑力矩，其值为 c·AC·R，c为土的粘聚力；另一项是滑动 土体重量在滑动面上的反力所产生的抗 滑力矩。当土体的内摩擦角=0时，滑动 面是一个光滑面，通过圆心O，不产生力 矩，因此抗滑力矩只有c·AC·R一项

定义稳定安全系数为：抗滑力矩MRC·AC.R(7 - 8)FM,Wd滑动力矩5

5 ◼ 定义稳定安全系数为： (7 -8) Wd c AC R M M F s R s • • = = = 滑动力矩 抗滑力矩

二、条分法的基本概念■为了将圆弧滑动法应用于Φ>0的粘性土，通常采用条分法。条分法就是将滑动土体竖直分成若干土条，把土条当成刚体，分别求作用于各土条上的力对圆心的滑动力矩和抗滑力矩，然后按式（7一8）求土坡的稳定安全系数。6

6 二、条分法的基本概念 ◼ 为了将圆弧滑动法应用于＞0的粘性土， 通常采用条分法。 ◼ 条分法就是将滑动土体竖直分成若干土 条，把土条当成刚体，分别求作用于各 土条上的力对圆心的滑动力矩和抗滑力 矩，然后按式（7－8）求土坡的稳定安 全系数

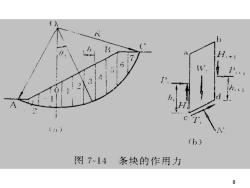
作用在条块i上的力有重力W、条块侧面的法向力P.和P+,以及切向力H和Hi+1（图7一14）。P和P+的作用点离弧面分别为h,和hi+1。滑弧段cd（长度为l）上的法向力N,和切向力T，T中包括粘聚阻力c.l和摩擦阻力Ntgd;。由于条块的宽度不大，W和N.可以看成作用于弧段cd的中点。7

7 ◼ 作用在条块i上的力有重力Wi、条块侧面 的法向力Pi和Pi+1以及切向力Hi和Hi+1（图 7－14 ）。Pi和Pi+1的作用点离弧面分别 为hi和hi+1。滑弧段cd（长度为l i）上的法 向力Ni和切向力Ti，Ti中包括粘聚阻力ci l i 和摩擦阻力Ni·tgi。由于条块的宽度不大， Wi和Ni可以看成作用于弧段cd的中点

T8H.+1Vih.tIdhAi(a)八(b)[图 7~14 条块的作用力8

8

■在这些力中，P.、N.和h在分析前一土条时已经出现，可视为已知量，因此待定的未知量有Pi+1、Ni+1、hi+1、N,和T,共5个。每个土条可建立两个静力平衡方程F=0，F,=0、一个力矩平衡方程ZM,=0和一个极限平衡方程T,=Ntgg+clF因此条分法是一个高次的超静定问题。9

9 ◼ 在这些力中，Pi、Ni和hi在分析前一土条 时已经出现，可视为已知量，因此待定 的未知量有Pi+1、Ni+1、hi+1、Ni和Ti共5个。 每个土条可建立两个静力平衡方 程 、一个力矩平衡方 程 和一个极限平衡方程 。 因此条分法是一个高次的超静定问题。 Fxi = 0， Fzi = 0 Mi = 0 s i i i i i F N tg c l T + = 

各种简化假定大体上分为三种类型：（1）不考虑条块间作用力或仅考虑其中一个。瑞典条分法和简化毕肖普法属于此类;（2）假定条间力的作用方向或规定P.和H的比值。前述的折线滑动面分析方法属于这一类；（3）假定条块间力的作用位置即规定h的大小。普遍条分法属于这一类。10

10 ◼ 各种简化假定大体上分为三种类型： （1）不考虑条块间作用力或仅考虑其中一 个。瑞典条分法和简化毕肖普法属于此 类； （2）假定条间力的作用方向或规定Pi和Hi 的比值。前述的折线滑动面分析方法属 于这一类； （3）假定条块间力的作用位置即规定hi的 大小。普遍条分法属于这一类