《土力学与地基基础》课程教学课件（PPT讲稿）第六章 挡土结构物上的土压力 第四节 库伦土压力理论 第五节 坦墙土压力的计算 第六节 朗肯理论与库伦理论的比较 第七节 几种常见情况的主动土压力计算

第四节库伦土压力理论■库伦（1776）根据墙后土楔体处于极限平衡状态时的力系平衡条件，提出了另一种土压力分析方法。库伦土压力理论适用于各种填土面和不同的墙背条件，目方法简便，有足够的计算精度。1

1 第四节 库伦土压力理论 ◼ 库伦（1776）根据墙后土楔体处于极限 平衡状态时的力系平衡条件，提出了另 一种土压力分析方法。库伦土压力理论 适用于各种填土面和不同的墙背条件， 且方法简便，有足够的计算精度

一、方法要点（一）库伦公式推导的出发点■在挡土墙及填土的边界条件上，库伦理论者虑的挡干墙，可以是墙背倾斜（倾角为α）：墙背粗糙，墙背与填土之间存在摩擦力（摩擦角为）；墙后填王面有倾角β。■库伦理论从考虑墙后某个滑动土楔体的整体平衡条件出发，直接求出作用在墙背上的总土压力E。2

2 一、方法要点 （－）库伦公式推导的出发点 ◼ 在挡土墙及填土的边界条件上，库伦理 论考虑的挡土墙，可以是墙背倾斜（倾 角为）；墙背粗糙，墙背与填土之间存 在摩擦力（摩擦角为）；墙后填土面有 倾角。 ◼ 库伦理论从考虑墙后某个滑动土楔体的 整体平衡条件出发，直接求出作用在墙 背上的总土压力E

（二）库伦假设条件平面滑裂面假设。刚体滑动假设。1土楔体ABC整体处于极限平衡状态

3 （二）库伦假设条件 ◼ 平面滑裂面假设。 ◼ 刚体滑动假设。 ◼ 土楔体ABC整体处于极限平衡状态

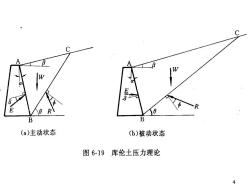
tBB(a)主动状态(b）被动状态图6-19库伦土压力理论

4

（三）滑动土楔体的受力分析■根据土楔体整体处于极限平衡状态的条件，可得知E、R的方向。根据楔体应满足静力平衡力三角形闭合的条件，可知E、R的大小。■求极值，找出真正滑裂面，从而得出作用在墙背上的总主动土压力E,和被动土压力Ep。5

5 （三）滑动土楔体的受力分析 ◼ 根据土楔体整体处于极限平衡状态的条 件，可得知E、R的方向。 ◼ 根据楔体应满足静力平衡力三角形闭合 的条件，可知E、R的大小。 ◼ 求极值，找出真正滑裂面，从而得出作 用在墙背上的总主动土压力Ea和被动土 压力Ep

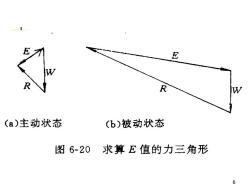
E 7EWKRW(a）主动状态(b)被动状态图6-20求算E值的力三角形6

6

为了找出土中真正的滑裂面，可假设不同0角的几个滑裂面，分别算出维持各个滑裂楔体保持极限平衡时的土压力E值。对于主动状态来说，要求E值最大的滑裂面是真正的滑裂面；对于被动状态来说，需要E值最小的滑裂面是真正的滑裂面。利用dE/dO=0条件，即可求得作用于挡土墙上的总土压力E,或E

7 ◼ 为了找出土中真正的滑裂面，可假设不 同角的几个滑裂面，分别算出维持各个 滑裂楔体保持极限平衡时的土压力E值。 对于主动状态来说，要求E值最大的滑裂 面是真正的滑裂面；对于被动状态来说， 需要E值最小的滑裂面是真正的滑裂面。 利用dE/d=0条件，即可求得作用于挡土 墙上的总土压力Ea或Ep

二、数解法（一）无粘性土的主动土压力设挡土墙（图6一21a）墙高为H，墙后为无粘性填土。潜在滑动面BC与水平面夹角为0。根据静力平衡条件，作用于隔离体ABC上的力W、E、R组成力的闭合三角形（图6一21b）。根据几何关系可知，W与E之间的夹角=90°-S-α为常数；W与R之间的夹角为0-Φ8

8 二、数解法 （一）无粘性土的主动土压力 ◼ 设挡土墙（图6－21a）墙高为H，墙后为 无粘性填土。潜在滑动面BC与水平面夹 角为。根据静力平衡条件，作用于隔离 体ABC上的力W、E、R组成力的闭合三 角形（图6－21b）。根据几何关系可知， W与E之间的夹角=90o --为常数；W 与R之间的夹角为-

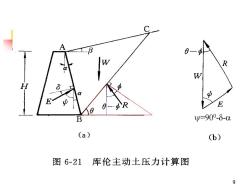
A6IwRWH8EFSR10=900-8-αB(a)(b)图6-21库伦主动土压力计算图9

9 =900 --

利用正弦定律可得：EWsin( 0 -Φ)sin[180° -(0-Φ+y)W sin(0-Φ)即E=(6 - 20)sin(θ-Φ+y)1土楔体自重W是0的函数，故当和值为定值后，E只是0的单值函数，即E=f()。10

10 ◼ 利用正弦定律可得： ◼ 土楔体自重W是的函数，故当和值为 定值后，E只是的单值函数，即E=f()。 (6 - 20) sin( ) sin( ) sin( ) sin[180 ( )           − + − = − − + = − W E E W o 即