北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 6-3

*二线性子空间 1.定义V是数域P上的线性空间,W是V的非 空子集合,对于'中定义的两种运算仍然构成一个线 性空间,称W是V的线性子空间,简称子空间。 定理W是数域P上线性空间V的非空子集合,则 W是V的线性子空间 的充分必要条件是:W对V中定义的加法和数乘运算是 封闭的。 即是V的线性子空间要满足三条: (1)W是非空集; (2)若a,B∈W→a田B∈W: (3)若k∈P,a∈W,→ka∈W
* 二 线性子空间 1.定义 V 是数域 P上的线性空间,W 是V 的非 空子集合,对于V 中定义的两种运算仍然构成一个线 性空间,称W 是V 的线性子空间,简称子空间。 定理 W 是数域P上线性空间V 的非空子集合,则 W 是V 的线性子空间 的充分必要条件是:W 对V 中定义的加法和数乘运算是 封闭的。 即是V 的线性子空间要满足三条: (1)W 是非空集; (2)若 , W W ; (3)若 k P, W, k W

2.子空间的交与和 子空间的交:设W,W,是V的两个子空 间,则W,W,公共元素的集合 W⌒W,={aa∈W&a∈W,} 可以证明W⌒W,也是V的子空间,称为W,W, 的交。 * 子空间的和:设W,W,是V的两个子空 间,则集合 W+W,={a+02o,∈W,a2∈W2} 是V的子空间,称为W,W,的和。 上页 返回
2.子空间的交与和 * 子空间的交:设 1 2 W , W 是V 的两个子空 间,则 1 2 W , W 公共元素的集合 { & } W1W2 = W1 W2 可以证明W1W2也是V 的子空间,称为 1 2 W , W 的交。 * 子空间的和:设 1 2 W , W 是V 的两个子空 间,则集合 { , } W1 +W2 = 1 +2 1W1 2W2 是V 的子空间,称为 1 2 W , W 的和

例 V={aa=(a,a2,a)',a∈R}是线性空间 W={BB=(0,b,b)',b,∈R是V线性子 空间 W,={Yy=(c,0,0),c∈R是V线性子 空间 几何表示: V={aa=(a,a2,a)',a∈R 上页 区回
例 { ( , , ) , } V a1 a2 a3 aj R T = = 是线性空间 { (0, , ) , } W1 b1 b2 bj R T = = 是V 线性子 空间 { ( , 0, 0) , } W2 c c R T = = 是V 线性子 空间 几何表示:{ ( , , ) , } V a1 a2 a3 aj R T = = 0 Y Z

V=W+W, 0=W∩W 直和:假设两个子空间的交是 {0}空间,那么它们的和称为 直和。在上个例子中 0=W⌒W2 所以 V=W+W2,是直和,记为: V=W⊕W, 上页 返回
W1 0 V =W1 +W2 0 =W1W2 直和:假设两个子空间的交是 {0} 空间,那么它们的和称为 直和。在上个例子中 0 =W1W2 所以 V =W1 +W2 ,是直和,记为: V =W1W2
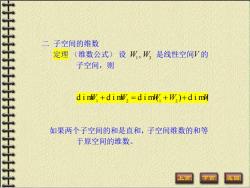
二子空间的维数 定理 (维数公式)设W,W,是线性空间V的 子空间,则 d in +din,=d im +)+d i m 如果两个子空间的和是直和,子空间维数的和等 于原空间的维数。 上页
二 子空间的维数 定理 (维数公式) 设 1 2 W , W 是线性空间V 的 子空间,则 dim dim dim( ) dim( ) W1 + W2 = W1 +W2 + W1W2 如果两个子空间的和是直和,子空间维数的和等 于原空间的维数
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 第二节 基坐标及其变换.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 第一节 线性空间的定义与性质.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第五章 二次型 第三节 正定二次型.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第五章 二次型 第二节 化二次型为标准型 一,正交替换法 二,配方法 三,初等变换法.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第五章 二次型 第一节 二次型及其矩阵表示.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第四节 实对称矩阵的对角化.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第三节 向量的内积和Schmidt正交化.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第二节 相似矩阵和矩阵对角化.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第一节 矩阵的特征值和特征向量.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第六节 线性方程组解的结构.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第五节 齐次线性方程组的解法.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第四节 矩阵秩与向量组秩的关系.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第三节 向量组的秩.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第二节 向量组的线性相关性.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第一节 n维向量及其运算.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第七节 矩阵的秩.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第六节 利用初等变换求逆矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第五节 分块矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第四节 逆矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第三节 特殊矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 6-4.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 6-5.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第一节 向量的内积与欧氏空间.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第二节 标准正交基.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第三节 正交变换.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第四节 向量到子空间的距离、最小二乘法.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第五节 酉空间介绍.ppt
- 《矩阵论》课程教学资源(书籍教材)研究生数学教学系列(工科类)矩阵论简明教程(编著:徐仲等).pdf
- 长沙理工大学:《矩阵论》课程教学资源(课件讲稿,打印版)第二章 范数理论(负责人:刘文军).pdf
- 长沙理工大学:《矩阵论》课程教学资源(课件讲稿,打印版)第四章 矩阵分解.pdf
- 长沙理工大学:《矩阵论》课程教学资源(课件讲稿,打印版)第三章 矩阵分析.pdf
- 长沙理工大学:《矩阵论》课程教学资源(课件讲稿,打印版)第一章 矩阵的相似变换.pdf
- 长沙理工大学:《高等代数与解析几何》课程教学资源(大纲教案)Advanced Algebra and Analytic Geometry.pdf
- 长沙理工大学:《高等代数与解析几何》课程教学资源(习题解答)一元多项式与整数的因式分解.pdf
- 长沙理工大学:《高等代数与解析几何》课程教学资源(习题解答)行列式.pdf
- 长沙理工大学:《高等代数与解析几何》课程教学资源(习题解答)线性方程组与线性子空间.pdf
- 长沙理工大学:《高等代数与解析几何》课程教学资源(习题解答)矩阵的秩与矩阵的运算.pdf
- 长沙理工大学:《高等代数与解析几何》课程教学资源(习题解答)坐标变换与点变换.pdf
- 长沙理工大学:《高等代数与解析几何》课程教学资源(习题解答)线性变换.pdf
- 长沙理工大学:《高等代数与解析几何》课程教学资源(习题解答)多项式矩阵与若尔当典范形.pdf
