北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第一节 n维向量及其运算

第三章 线性方程组 3.1维向量及其线性运算 3.2 线性相关性 3.3 向量组的秩 3.4 矩阵的秩 3.5 齐次线性方程组 3.6非齐次线性方程组
第三章 线性方程组 3.1 n维向量及其线性运算 3.2 线性相关性 3.3 向量组的秩 3.4 矩阵的秩 3.5 齐次线性方程组 3.6 非齐次线性方程组

第一节n维向量及其运算 定义1: 数域P上的n个有次序的数41,2,,m 所组成的有序数组 称为数域P上的一个 n 维向量(vector),其中心称为第i个分量。 以后我们用小写希腊字母Q,B,Y·来代表向量。 而用小写拉丁字母,b,C,·来代表数
定义1:数域P上的n 个有次序的数 所组成的有序数组 称为数域P上的一个 n 维向量(vector), 其中 称为第 i 个分量。 1 2 , , , n a a a ( ) 1 2 , , , n a a a i a 以后我们用小写希腊字母 , , 来代表向量。 而用小写拉丁字母 a,b,c, 来代表数。 第一节 n 维向量及其运算

a=(a,a2,,an也称为n维行向量 0 称为n维列向量 分量全为零的向量(0,0,…,0 称为零向量。 注:一个n维行向量就是一个1×n矩阵; 一个n维列行向量就是一个nx1矩阵,故 a =(a,4,,a)
= (a1 ,a2 , ,an )也称为n维行向量 称 为n维列向量 a a a n = 2 1 分量全为零的向量 (0,0, ,0) 称为零向量。 一个 维列行向量就是一个 矩阵 故 注:一个 维行向量就是一个 矩阵; 1 , 1 n n n n ( ) T n n a a a a a a , , , 1 2 2 1 =

例: ()n个未知量的任一齐次线性方程组的每一个 解都是一个每一个解都是一个维向量,且其几 个解的线性组合仍是齐次线性方程组的解。 (2)一个×n矩阵的每一行都是一个n维向量, 而它的每一列都是m维向量;反之,将m个n 维向量按行排列,就可构成一个m×n矩阵。将 n个m维向量按列排列,就可构成一个m×n矩 阵
例: (1) n个未知量的任一齐次线性方程组的每一个 解都是一个每一个解都是一个n维向量,且其几 个解的线性组合仍是齐次线性方程组的解。 (2) 一个 m× n 矩阵的每一行都是一个 n 维向量, 而它的每一列都是 m 维向量;反之,将 m 个 n 维向量按行排列,就可构成一个 m× n 矩阵。将 n个 m 维向量按列排列,就可构成一个m× n 矩 阵

定义2如果a=(a,,…,an)和B=(b,b,,b) 是两个维向量,如果他们的对应分量都相等 即a,=b: (i=1,2,,n),则称向量a和B 相等,记做:a=B。 定义3 如果a=(41,,,an)和B=((亿,b,,b)》 是两个n维向量,则c与B的和a+B为 a+B=(a1+b,a2+b2,…,an+bn) 负向量:向量-C=(一4,一a2,,一am 称为向量的负向量 向量的差:a-B=a+(-β)
定义2 如果 和 是两个 n 维向量,如果他们的对应分量都相等, 即 , 则称向量 和 相等,记做: = 。 ( ) 1 2 , , , n = a a a ( ) 1 2 , , , n = b b b 1,2, , ( ) i i a b i n = = 定义3 如果 和 是两个n 维向量,则与的和 + 为: ( ) 1 2 , , , n = a a a ( ) 1 2 , , , n = b b b ( , , , ) 1 1 2 2 n n + = a + b a + b a + b 负向量:向量 称为向量的负向量; ( , , , ) 1 2 n − = −a −a −a 向量的差: − = + (−)

数乘运算:设k为数域P中的数,向量 (ka,ka,,ka,)称为向量a=(a,4,,a,) 与数k的数量乘积。记为ka。 数乘运算满足下列四条规则: (1)1ox=c (2)k(la)=(k)a (3)(k+1a=ka+la (4)k(a+B)=ka+kB Q,B是n维向量,k,l∈P
数乘运算:设 k 为数域 P 中的数,向量 ( ) 1 2 , , , n ka ka ka 称为向量 ( ) 1 2 , , , n = a a a 与数 k 的数量乘积。记为 k 。 数乘运算满足下列四条规则: ( ) n k l P k k k k l k l k l k l + = + + = + = = , , (4) ( ) (3) (2) ( ) ( ) (1)1 是 维向量,

加法运算满足性质 (5)a+B=B+a (6(a+)+y=(a+B)+ (7)a+0=c (8)a+(a)=0 注 ·零向量和负向量是唯一的 ·加法的逆运算是减法
(8) ( ) 0 (7) 0 (6)( ) ( ) (5) + − = + = + + = + + + = + 加法运算满足性质 注: • 零向量和负向量是唯一的 •加法的逆运算是减法

线性运算:上述向量的加法及数乘运算称为向量 的线性运算。 注: 满足上述(1)一(8)的运算称为线性运算。 1)0a=0 (2)(-1)a=-C, (3)20=0 (4)如果ka=0,则k=0或a=0
线性运算:上述向量的加法及数乘运算称为向量 的线性运算。 注: •满足上述 (1)–(8) 的运算称为线性运算。 (4) 0, 0 0 (3) 0 0. (1) 0 0 (2) ( 1) ; = = = = = − = − 如果k 则k 或
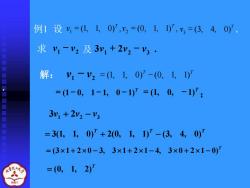
例1设y=(L10),y2=(0,1,1),y3=(3,4,0) 求1-2及3y1+2y2-V· 解:y-y2=(1,10)-(0,1,1) =0-0,1-1,0-1)=(1,0,-1); 3y1+2y2- =31,1,0)+2(0,1,1)'-3,4,0) =(3×1+2×0-3,3×1+2×1-4,3×0+2×1-0) =(0,1,2)1
例1 设 (1, 1, 0) , (0, 1, 1) , 1 2 T T v = v = T v (3, 4, 0) 3 = , 求 1 2 v − v 及 1 2 3 3v + 2v − v . 解: 1 2 v − v T T = (1, 1, 0) − (0, 1, 1) T = (1 − 0, 1 − 1, 0 − 1) T = (1, 0, − 1) ; . 3 1 2 2 3 v + v − v T T T = 3(1, 1, 0) + 2(0, 1, 1) − (3, 4, 0) T = (31 + 2 0 − 3, 31 + 21 − 4, 3 0 + 21 − 0) T = (0, 1, 2)

例2.设3(a1-a)+2(a2+a)=5(a3+a) 其中a1=(2,5,1,3)a2=(10,1,5,10) a3=(4,1,-1,1)7,求a 解:由3(a,-a)+2(a2+a)=5(a3+a 整理得 a=63a+2a-5a =325,13+2101,510-541,-1,1y] =(1,2,3,4)7
例 2.设 3( ) 2( ) 5( ) 1 2 3 a − a + a + a = a + a 其中 T a (2,5,1,3) 1 = , T a (10,1,5,10) 2 = , T a (4,1, 1,1) 3 = − , 求 a 解: 由 3( ) 2( ) 5( ) 1 2 3 a − a + a + a = a + a 整理得 (3 2 5 ) 6 1 a a1 a2 a3 = + − [3(2,5,1,3) 2(10,1,5,10) 5(4,1, 1,1) ] 6 1 T T T = + − − T = (1,2,3,4)
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第七节 矩阵的秩.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第六节 利用初等变换求逆矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第五节 分块矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第四节 逆矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第三节 特殊矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第二节 矩阵的运算.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第一节 高斯消元法与矩阵的初等变换.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 第五节 克莱姆法则.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 第四节 行列式按行(列)展开.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 第三节 行列式的性质.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 第一节 二阶与三阶行列式 第二节 n阶行列式的的定义.ppt
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第7章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第6章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第5章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第4章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第3章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第2章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第1章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)2008——2009学年第二学期《线性代数(48学时)》考试试卷.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)2008——2009学年第二学期《线性代数(40学时)》考试试卷.doc
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第二节 向量组的线性相关性.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第三节 向量组的秩.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第四节 矩阵秩与向量组秩的关系.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第五节 齐次线性方程组的解法.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第六节 线性方程组解的结构.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第一节 矩阵的特征值和特征向量.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第二节 相似矩阵和矩阵对角化.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第三节 向量的内积和Schmidt正交化.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第四节 实对称矩阵的对角化.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第五章 二次型 第一节 二次型及其矩阵表示.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第五章 二次型 第二节 化二次型为标准型 一,正交替换法 二,配方法 三,初等变换法.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第五章 二次型 第三节 正定二次型.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 第一节 线性空间的定义与性质.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 第二节 基坐标及其变换.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 6-3.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 6-4.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 6-5.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第一节 向量的内积与欧氏空间.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第二节 标准正交基.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第三节 正交变换.ppt
