北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第五节 齐次线性方程组的解法

第五节 齐次线性方程组的解法 ~齐你线性方腥组解的性质 >基础解系及其求法
第五节 齐次线性方程组的解法 ➢ 齐次线性方程组解的性质 ➢基础解系及其求法

,齐次线性方程组解的性质 1。解向量的概念 设有齐次线性方程组 011+0122++a1nXn=0 02131+422少2+…+42mXn=0 (1 0m心1+0m22+…+ann=0 写成矩阵形式为 A4x=0. 其中 A=( 为(1)的系数矩阵
一.齐次线性方程组解的性质 设有齐次线性方程组 + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x (1 写成矩阵形式为 Ax = 0. A (a ) ij mn 其中 = 为(1)的系数矩阵, 1.解向量的概念

X= 称为方程组(1)的解向量,亦即方程组(1)的 解。 2,齐次线性方程组解的性质 (1)若x=51,x=52为Ax=0的解,则 x=51+52 也是Ax=0的解, 证明A51=0,A5=0 ∴.A(5+5)=A5+A52=0
= n x x x x 2 1 A 1 = 0, A 2 = 0 称为方程组(1)的解向量,亦即方程组(1)的 解。 2.齐次线性方程组解的性质 (1)若 x = 1 ,x = 2 为 Ax = 0 的解,则 x = 1 + 2 也是 Ax = 0 的解. 证明 A( 1 + 2 ) = A 1 + A 2 = 0

故x=5气+52也是Ax=0的解 (2)若x=5为Ax=0的解,k为实数,则 x=k5也是Ax=0的解. 证明A(k5)=kA(5)=k0=0. 证毕
0 . 故 x =1 + 2 也是Ax = 的解 ( 2)若 为 的解, 为实数,则 也是 的解. x = 1 Ax = 0 k x = k 1 Ax = 0 证明 A(k ) kA( ) k 0 0. 1 = 1 = = 证毕

二、 基础解系及其求法 1。基础解系的定义 01,2,…,7,称为齐次线性方程组Ax=0的基础 解系,如果 (1)门1,12,…,1是Ax=0的一组线性无关的解; 如果1,2,,,为齐次线性方程组Ax=0 的一组基础解系,那么,Ax=0的通解可表示为
1.基础解系的定义 二、基础解系及其求法 解系 如果 称为齐次线性方程组 的基础 , h1 ,h 2 ,,h t Ax = 0 (1) , , , 0 ; h 1 h 2 h t是Ax = 的一组线性无关 的解 的一组基础解系 那么 的通解可表示为 如果 为齐次线性方程组 0 = = Ax t Ax , , h1 ,h2 ,,h 0

x=kh1+k22+…+k,n 其中k1,k2,,k,是任意常数 2,线性方程组基础解系的求法 定理 若齐次线性方程组的系数矩阵A的秩 R(A)片<n(未知量的个数),则(1)必有基础解系: 且基础解系中含有n-r个解向量. 证明 因R(A)戶<n,则A可经有限次初等行变换和列 的换法变换化为B型阵,即
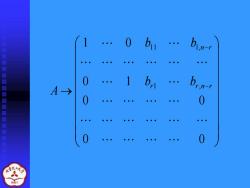
t t x = k1h1 + k2h2 ++ k h , , , . 其中k1 k2 kn−r是任意常数 2.线性方程组基础解系的求法 定理 若齐次线性方程组的系数矩阵A的秩 R(A)=r<n(未知量的个数),则(1)必有基础解系; 且基础解系中含有n-r个解向量. 证明 因R(A)=r<n,则A可经有限次初等行变换和列 的换法变换化为B型阵,即 .
0b1…bnr 0 A- r.n-r 0
→ − − 0 0 0 0 0 1 1 0 1 , 1 1 1, r r n r n r b b b b A
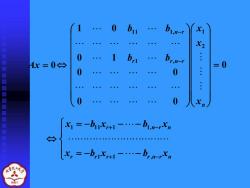
1 bin-r 2 0 b 4x=0台 :.: =0 0 0 0 0 =-b心+1--bn-n x=-b-brn
0 0 0 0 0 0 1 1 0 2 1 1 , 1 1 1, = − − n r r n r n r x x x b b b b = − − − = − − − + − + − r r r r,n r n r ,n r n x b x b x x b x b x 1 1 1 1 1 1 1 Ax = 0

现对x,41,,心n取下列n一r组数: 1=-b1X+1--b1-x2 分别代入 =br1br-rn
现对 x r+1 , , x n 取下列 n− r 组数: + + n r r x x x 2 1 = − − − = − − − + − + − r r r r,n r n r ,n r n x b x b x x b x b x 1 1 1 1 1 1 1 分别代入 , . 1 0 0 , 0 1 0 , = 0 0 1
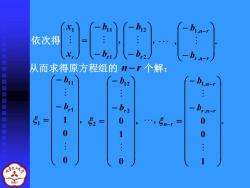
依次得 从而求得原方程组的n一P个解: bi b12 bi.n-r b b:2 5 1 52= 0 5- 0 0 0 0
依次得 xr x 1 , b b r − − = 0 0 1 1 11 1 , 0 1 0 2 12 2 − − = br b . b b r,n r ,n r n r − − = − − − 1 0 0 1 从而求得原方程组的 n− r 个解: . b b , r,n r ,n r − − − − 1 , b b r − − 2 12 , b b r − − = 1 11
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第四节 矩阵秩与向量组秩的关系.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第三节 向量组的秩.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第二节 向量组的线性相关性.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第一节 n维向量及其运算.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第七节 矩阵的秩.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第六节 利用初等变换求逆矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第五节 分块矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第四节 逆矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第三节 特殊矩阵.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第二节 矩阵的运算.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵 第一节 高斯消元法与矩阵的初等变换.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 第五节 克莱姆法则.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 第四节 行列式按行(列)展开.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 第三节 行列式的性质.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 第一节 二阶与三阶行列式 第二节 n阶行列式的的定义.ppt
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第7章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第6章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第5章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第4章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(试卷习题)《线性代数》第3章习题解答.doc
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第三章 线性方程组 第六节 线性方程组解的结构.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第一节 矩阵的特征值和特征向量.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第二节 相似矩阵和矩阵对角化.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第三节 向量的内积和Schmidt正交化.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第四章 矩阵的对角化 第四节 实对称矩阵的对角化.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第五章 二次型 第一节 二次型及其矩阵表示.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第五章 二次型 第二节 化二次型为标准型 一,正交替换法 二,配方法 三,初等变换法.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第五章 二次型 第三节 正定二次型.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 第一节 线性空间的定义与性质.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 第二节 基坐标及其变换.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 6-3.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 6-4.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第六章 线性空间与线性变换 6-5.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第一节 向量的内积与欧氏空间.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第二节 标准正交基.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第三节 正交变换.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第四节 向量到子空间的距离、最小二乘法.ppt
- 北京化工大学:《线性代数》课程教学资源(PPT课件)第七章 欧氏空间 第五节 酉空间介绍.ppt
- 《矩阵论》课程教学资源(书籍教材)研究生数学教学系列(工科类)矩阵论简明教程(编著:徐仲等).pdf
- 长沙理工大学:《矩阵论》课程教学资源(课件讲稿,打印版)第二章 范数理论(负责人:刘文军).pdf
