《数学教学论》课程教学资源（初等几何研究讲义）第十七讲 体积的概念、求立体体积的基础

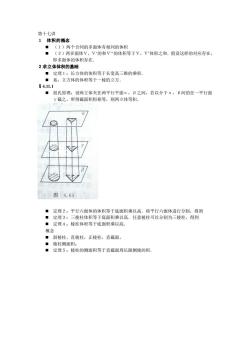
第十七讲 1体积的概念 (1)两个合同的多面体有相同的体积 ■（2)两多面体V,V的和V的体积等于V,V体积之和。假设这样的对应存在， 即多面体的体积存在。 2求立体体积的基础 ■定理1：长方体的体积等于长宽高三维的乘积 ■系：立方体的体积等于一棱的立方 4.11.1 ·祖氏原理：设两立体夹在两平行平面a，B之间，若以介于a,B间的任一平行面 Y截之，所得截面积恒相等，则两立体等积. Y 图4.633 ■定理2：平行六面体的体积等于底面积乘以高。将平行六面体进行分割，得到 ■定理3】 三棱柱体积等于底面积乘以高。任意棱柱可以分割为三棱柱，得到 。定理4：棱柱体积等于底面积乘以高。 概念 ■斜棱柱，直棱柱，正棱柱，直截面， ■枝柱侧面积： ■定理5：棱柱的侧面积等于直截面周长跟侧棱的积

第十七讲 １ 体积的概念 ◼ （１）两个合同的多面体有相同的体积 ◼ （２）两多面体Ｖ，Ｖ‘的和Ｖ’‘的体积等于Ｖ，Ｖ’体积之和．假设这样的对应存在， 即多面体的体积存在． ２求立体体积的基础 ◼ 定理１：长方体的体积等于长宽高三维的乘积． ◼ 系：立方体的体积等于一棱的立方． §4.11.1 ◼ 祖氏原理：设两立体夹在两平行平面α，β之间，若以介于α，β间的任一平行面 γ截之，所得截面积恒相等，则两立体等积． ◼ 定理２：平行六面体的体积等于底面积乘以高．将平行六面体进行分割，得到 ◼ 定理３：三棱柱体积等于底面积乘以高．任意棱柱可以分割为三棱柱，得到 ◼ 定理４：棱柱体积等于底面积乘以高． 概念 ◼ 斜棱柱，直棱柱，正棱柱，直截面， ◼ 棱柱侧面积： ◼ 定理５：棱柱的侧面积等于直截面周长跟侧棱的积．

图4.66 8411.2棱锥 ■棱锥的定义 ■正棱锥，斜高 ·定理6：正棱锥的侧面积等于底面周长与斜高乘积的一半. ■定理7：棱锥被平行于底面的平面所截截口多边形相似于底面，面积比等于从锥顶 到截面的距离与锥高的平方比. ■系： ■定理8： 三棱锥的体积公式： §4.1山.3棱台 ■1概念： ■2定理9：正棱台的侧面积等于两底周长的半和与斜高的积 ■3定理10：棱台的体积公式 V=(S++)h 拟柱体积 ■1拟柱（体）的定义： ·拟柱的特例 2拟柱的体积 ·分割一计算一求和一取极限 -(5

§4.11.２ 棱锥 ◼ 棱锥的定义 ◼ 正棱锥，斜高 ◼ 定理６：正棱锥的侧面积等于底面周长与斜高乘积的一半． ◼ 定理７：棱锥被平行于底面的平面所截截口多边形相似于底面，面积比等于从锥顶 到截面的距离与锥高的平方比． ◼ 系： ◼ 定理８：三棱锥的体积公式： §4.11.３ 棱台 ◼ １ 概念： ◼ ２ 定理９：正棱台的侧面积等于两底周长的半和与斜高的积 ◼ ３ 定理１０：棱台的体积公式 拟柱体积 ◼ １ 拟柱（体）的定义： ◼ 拟柱的特例 ◼ ２ 拟柱的体积 ◼ 分割→计算→求和→取极限 1 1 1 ( ) 3 V S SS S h = + +1 1 ( 4 ) 6 V S M S h = + +

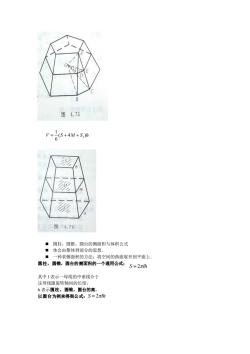
图4.73 V-1(S+4M+S)h 图4.74 ■圆柱，圆锥，圆台的侧面积与体积公式 ■体会由整体到部分的思想 一种求侧面积的方法：将空间的曲面展开到平面上 圆柱，圆锥，圆台的侧面积的一个通用公式：S=2xh 其中1表示一母线的中垂线介于 这母线跟旋转轴间的长度， h表示圆柱，圆锥，台的高 以圆台为例来得到公式：S=2πW

◼ 圆柱，圆锥，圆台的侧面积与体积公式 ◼ 体会由整体到部分的思想． ◼ 一种求侧面积的方法：将空间的曲面展开到平面上． 圆柱，圆锥，圆台的侧面积的一个通用公式： 其中 l 表示一母线的中垂线介于 这母线跟旋转轴间的长度， h 表示圆柱，圆锥，圆台的高． 以圆台为例来得到公式： 1 1 ( 4 ) 6 V S M S h = + + S lh = 2 S lh = 2

班承 图475 球→球带，球冠，球缺，球扇形 ·1球带的概念 ■2球带面积的计算（分割一计算一求和一取极限） ■定理11：球带的面积公式 S球带=2πh 图4.76 ■系：同球的两个球带面积之比等于他们的高之比 ■定理12：球的表面积等于大圆面积的4倍 球扇形，球，球缺的体积 (部分→整体→部分) a 4.77

球→球带，球冠，球缺，球扇形 ◼ １ 球带的概念 ◼ ２ 球带面积的计算（分割→计算→求和→取极限） ◼ 定理１１：球带的面积公式 ◼ 系：同球的两个球带面积之比等于他们的高之比． ◼ 定理１２：球的表面积等于大圆面积的４倍 球扇形，球，球缺的体积 （部分→整体→部分） S rh 球带 = 2 2 1 3 2 3 V S r  r h =  = 球扇 球带

球缺的体积 ■球缺的概念 ■球缺的体积公式 ■定理15：设球半径为r,球缺的高为h则球缺的体积为： 装=h(-名

球缺的体积 ◼ 球缺的概念 ◼ 球缺的体积公式 ◼ 定理１５：设球半径为 r，球缺的高为 h,则球缺的体积为： 2 ( ) 3 h V h r 球缺 = − 