厦门大学：《结构化学 Structural Chemistry》课程教学资源（课件讲稿）Chapter 4 The structure of diatomic molecules

What's a chemical bond? Chemical Bonding

What’s a chemical bond? Chemical Bonding

Quantum mechanical theory for description of molecular structures and chemical bondings Molecular Orbital (MO)Theory a)Proposed by Hund,Mulliken,Lennard-Jones et al.in 1930s. b)Further developments by Slater,Huckel and Pople et al c)MO-based softwares are widely used nowaday,e.g.,Gaussian Valence Bond (VB)Theory a)Proposed by Heitler and London 1930s,further developments by Pauling and Slater et al. b)Programmed in later 1980s,e.g.,latest development--XMVB! Density Functional Theory a)Proposed by Kohn et al. b)DFT-implemented QM softwares are widely used,e.g.,Gaussian

Quantum mechanical theory for description of molecular structures and chemical bondings • Molecular Orbital (MO) Theory a) Proposed by Hund, Mulliken, Lennard-Jones et al. in 1930s. b) Further developments by Slater, Hückel and Pople et al. c) MO-based softwares are widely used nowaday, e.g., Gaussian • Valence Bond (VB) Theory a) Proposed by Heitler and London 1930s, further developments by Pauling and Slater et al. b) Programmed in later 1980s, e.g., latest development--XMVB! • Density Functional Theory a) Proposed by Kohn et al. b) DFT-implemented QM softwares are widely used, e.g., Gaussian

Slater Pauling Kohn 卢嘉锡

Slater Pauling Kohn 卢嘉锡

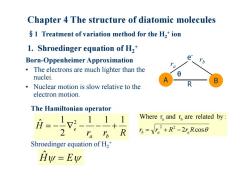
Chapter 4 The structure of diatomic molecules $1 Treatment of variation method for the H,+ion 1.Shroedinger equation of H,* Born-Oppenheimer Approximation e The electrons are much lighter than the 0 nuclei. Nuclear motion is slow relative to the R electron motion. The Hamiltonian operator 月=-12-111 Where r and r are related by: 2 ra I R 5=V.2+R2-2r.Rc0s0 Shroedinger equation of H2 Hy=Ew

Chapter 4 The structure of diatomic molecules §1 Treatment of variation method for the H 2 + ion 1. Shroedinger equation of H 2 + Born-Oppenheimer Approximation • The electrons are much lighter than the nuclei. • Nuclear motion is slow relative to the electron motion. r r R H a b e 1 1 1 2 1 ˆ 2       The Hamiltonian operator 2 cos  Where r and r are related by : 2 2 a b rb  ra  R  ra R A B e- r b r a R  Hˆ   E Shroedinger equation of H 2 +

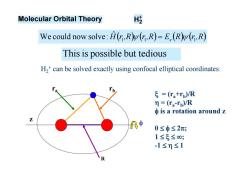
Molecular Orbital Theory H歧 We could now solve:H(,R(,R)=E.(R(r,R) This is possible but tedious H,+can be solved exactly using confocal elliptical coordinates: ξ=(Ta+rp)/R =(ra-rp)/R φis a rotation around z A中 0≤φ≤2； 1≤5≤0； -1≤m≤1

H2+ can be solved exactly using confocal elliptical coordinates: ra rb z  = (ra+rb)/R  = (ra-rb)/R  is a rotation around z 0  2; 1 ; -1  1 R  Molecular Orbital Theory H2 Hr,R  r,R E R r,R 1 1 e 1 ˆ We could now solve:    Thisis possible but tedious

Ψelee=F(传，n)(2π)l/neim吨 where m=0,±1，±2，±3， The associated quantum number is A.>orbital angular momentum 入=ml Each electronic level with m 0 is doubly degenerate,i.e.+ml,-m atoms:=0,1,2....and the atomic orbitals are called:s.p.d,etc. diatomics:入=0，l,2,.and the molecular orbitals are:o,元，δ，etc H2*:ro=2 Bohr letter Ep 2.71 eV

elec = F(,) (2)-1/2 eim where m=0, ±1, ±2, ±3, … The associated quantum number is .  orbital angular momentum  =|m| Each electronic level with m 0 is doubly degenerate, i.e. + |m|,-|m| atoms:  = 0,1,2,... and the atomic orbitals are called: s,p,d, etc. diatomics:  = 0,1,2, ... and the molecular orbitals are: , , , etc.  0 12 3 4 letter     H2+ : r0 = 2 Bohr Eb = 2.71 eV

2.The Variation Theorem For any well-behaved wavefunction the average energy from the Hamiltonian of the system is always greater or close to the exact ground state energy (Eo)for that Hamiltonian, E-9≥E ∫p"pdr

2. The Variation Theorem For any well-behaved wavefunction , the average energy from the Hamiltonian of the system is always greater or close to the exact ground state energy (E 0) for that Hamiltonian, * 0 * ˆ E d H d E           

Proof p(e≥Eo)its ground state(wo→Eo) p=∑cw Ψ1，Ψ2，Ψ3.consist of an A,=E,Ψ， E,≥E orthogonal normalized set of wavefunctions 「pidz = 「ppdx ∫idr=∑ciw,iΣc",dr=∑c∑c∫w,iwar =∑∑ccw,E",dr=∑∑cc,E,∫w,,d fpdr=∫∑cw,∑cw,dr=∑c,∑c∫g,w,dr =∑∑cc6, ∑∑cc,Ew,"dr∑efE E== ΣΣccA ∑s ≥E

2 0 * 2 * * * * * * * * * * * * * * 0 0 0 0 E ˆ ˆ ˆ ˆ ˆ ( ) its ( ) Proof                                                i i j i i i j ij i j i j j i j i j i j ij i j j i j j i i j j j i i i i j j i j i j i j i j j i j j i j j i i j j j i i i i i i i i i i c c E c c c c E d E c c d c c d c c d c c E d c c E d H d c H c d c c H d d H d E H E E E c E ground state E                                            ＝ ＝ ＝ 1, 2,  3 …consist of an orthogonal normalized set of wavefunctions

Example:Devise a trial variation function for the particle in a one-dimensional box of length I. A simple function that has the properties of the ground state is the parabolic function: 中=x(1-x) for0sx≤I 21 6m 0-a= -J "Hodr 5h2 >h2 8m12

Example: Devise a trial variation function for the particle in a one-dimensional box of length l. 0 l A simple function that has the properties of the ground state is the parabolic function:   x(l  x) for 0x l m l lx x dx dx d lx x m H d l 6 ( ) ( ) 2 ˆ 2 3 2 2 2 0 2 2 *             30 ( ) 5 2 0 2 * l d x l x dx l         2 8 2 2 2 4 2 5 * * ˆ ml h ml h d H d E             

3.Linear Variation Functions A linear variation function is a linear combination of =cf+c方++cnn=∑c,f n linearly independent functionsf2... Based on this principle,the parameters are regulated by the minimization routine so as to obtain the wavefunction that corresponds 82司 J0"odr to the minimum energy.This is taken to be the wavefunction that closely approximates 6= the ground state. adjusting the parameter, make 08 =0 aci

Based on this principle, the parameters are regulated by the minimization routine so as to obtain the wavefunction that corresponds to the minimum energy. This is taken to be the wavefunction that closely approximates the ground state. * 0 * ˆ E d H d E            adjusting the parameter, make  0   i c     E  3. Linear Variation Functions       n j n n j j c f c f c f c f 1 1 1 2 2  ... A linear variation function is a linear combination of n linearly independent functions f1, f2, …fn