中国科学技术大学：《数字几何处理 Digital Geometry Processing》课程教学资源（课件讲义）02 Discrete differential geometry

Discrete differential geometry Xiao-Ming Fu

Discrete differential geometry Xiao-Ming Fu

Goal Compute approximations of the differential properties of this underlying surface directly from the mesh data. Local Averaging Region ·Normal Vectors ·Gradients Laplace-Beltrami Operator ·Discrete Curvature

Goal • Compute approximations of the differential properties of this underlying surface directly from the mesh data. • Local Averaging Region • Normal Vectors • Gradients • Laplace-Beltrami Operator • Discrete Curvature

Local Averaging Region General idea:spatial averages over a local neighborhood (x)of a point x. ·x:one mesh vertex .(x):n-ring neighborhoods of mesh vertex or local geodesic balls. The size of the (x):stability and accuracy ·Large size:smooth Small size:accurate for clean mesh data

Local Averaging Region • General idea: spatial averages over a local neighborhood Ω(𝒙) of a point 𝒙. • 𝒙: one mesh vertex • Ω(𝒙): n-ring neighborhoods of mesh vertex or local geodesic balls. • The size of the Ω(𝒙): stability and accuracy • Large size: smooth • Small size: accurate for clean mesh data 𝒙

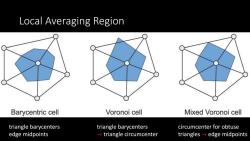
Local Averaging Region Barycentric cell Voronoi cell Mixed Voronoi cell triangle barycenters triangle barycenters circumcenter for obtuse edge midpoints triangle circumcenter triangles-edge midpoints

Local Averaging Region triangle barycenters edge midpoints triangle barycenters → triangle circumcenter circumcenter for obtuse triangles → edge midpoints

Implementation thinking How to compute the area of local average region?For example, barycentric cell. One simple idea:for each vertex,compute the area directly. ·Any improvement? How about Voronoi cell and mixed Voronoi cell?

Implementation thinking • How to compute the area of local average region? For example, barycentric cell. • One simple idea: for each vertex, compute the area directly. • Any improvement? • How about Voronoi cell and mixed Voronoi cell?

Normal Vectors Normal vectors for individual triangles are well-defined. Vertex normal:spatial averages of normal vectors in a local one-ring neighborhood. ∑Tea()arn(T) Zren()&rn(T)儿 1.constant weights:aT 1 2.triangle area:ar area(T) 3.incident triangle angles:a 0(T)

Normal Vectors • Normal vectors for individual triangles are well-defined. • Vertex normal: spatial averages of normal vectors in a local one-ring neighborhood. 𝒏 𝑣 = 𝑇∈Ω 𝑣 𝛼𝑇𝒏 𝑇 𝑇∈Ω 𝑣 𝛼𝑇𝒏 𝑇 2 1. constant weights: 𝛼𝑇 = 1 2. triangle area: 𝛼𝑇 = area(𝑇) 3. incident triangle angles: 𝛼𝑇 = 𝜃(𝑇)

Implementation thinking How to compute the normal on triangles or vertices?

Implementation thinking • How to compute the normal on triangles or vertices?

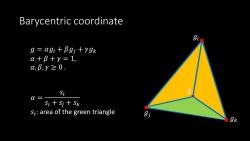
Barycentric coordinate g=agi+Bgi+ygk a+B+y=1, c,B,Y≥0. Si g Q= Si+Sj+Sk Si:area of the green triangle gk

Barycentric coordinate 𝑔 𝑖 𝑔 𝑗 𝑔 𝑘 𝑔 𝑔 = 𝛼 𝑔 𝑖 + 𝛽 𝑔 𝑗 + 𝛾 𝑔 𝑘 𝛼 + 𝛽 + 𝛾 = 1 , 𝛼 , 𝛽 , 𝛾 ≥ 0 . 𝛼 = 𝑠𝑖 𝑠𝑖 + 𝑠𝑗 + 𝑠 𝑘 𝑠 𝑖 : area of the green triangle

Gradients Given the function value on vertices,compute the gradient on each triangle. A piecewise linear function f(x)afi+Bfi+yfk X ·Gradient: Xk Vxf (x)=fiVa+fjVxB fkY Because ● l-2 A AT 2AT =(x-)·(xk-x)广/2Ar

Gradients • Given the function value on vertices, compute the gradient on each triangle. • A piecewise linear function 𝑓 𝒙 = 𝛼𝑓𝑖 + 𝛽𝑓𝑗 + 𝛾𝑓𝑘 • Gradient: 𝛻𝒙𝑓 𝒙 = 𝑓𝑖𝛻𝒙𝛼 + 𝑓𝑗𝛻𝒙𝛽 + 𝑓𝑘𝛻𝒙𝛾 • Because 𝛼 = 𝐴𝑖 𝐴𝑇 = 𝒙 − 𝒙𝑗 ∙ 𝒙𝑘 − 𝒙𝑗 ⊥ 𝒙𝑘 − 𝒙𝑗 2 𝒙𝑘 − 𝒙𝑗 2 2𝐴𝑇 = 𝒙 − 𝒙𝑗 ∙ 𝒙𝑘 − 𝒙𝑗 ⊥ /2𝐴𝑇 𝑓𝑖 𝑓𝑗 𝑓𝑘 𝒙𝑗 𝒙𝑘 𝒙𝑖 𝒙

Gradients 。Then Xi Ba (xk-xj) 2AT B= i-k) 2AT %xy (x-x) 2AT f(x)=f月 (+f (xj-xi) 2AT + 2AT 2AT

Gradients • Then 𝛻𝒙 𝛼 = 𝒙 𝑘 − 𝒙𝑗 ⊥ 2 𝐴 𝑇 𝛻𝒙 𝛽 = 𝒙 𝑖 − 𝒙 𝑘 ⊥ 2 𝐴 𝑇 𝛻𝒙 𝛾 = 𝒙𝑗 − 𝒙 𝑖 ⊥ 2 𝐴 𝑇 => 𝛻𝒙 𝑓 𝒙 = 𝑓𝑖 𝒙 𝑘 − 𝒙𝑗 ⊥ 2 𝐴 𝑇 + 𝑓𝑗 𝒙 𝑖 − 𝒙 𝑘 ⊥ 2 𝐴 𝑇 + 𝑓𝑘 𝒙𝑗 − 𝒙 𝑖 ⊥ 2 𝐴 𝑇 𝑓𝑖 𝑓𝑗 𝑓𝑘 𝒙𝑗 𝒙 𝑘 𝒙 𝑖 𝒙