上饶师范学院：《高等代数》课程教学资源（电子教案）高等代数电子教案（共六章）

数学与计算机系高等代数教研室 二零零二年五月 高等代数电子教案 第一章多项式 第一节数域 多项式是代数学中最基本的对象之一，它不但与高次方程的讨论有关，而且在进一步学习 代数以及其他数学分支时也会碰到。关于数的加、减、乘、除等运算的性质通常称为代数性 质。 定义1设P是由一些复数组成的集合，其中包括0与1。如果P中任意两个数（这两个 数也可以相同)的和、差、积商（除数不为零）仍然是P中的数，那么P就称为一个数域。 如果数的集合P中任意两个数作某一运算的结果都仍然在P中，我们就说数集P对这个运 算封闭的

数学与计算机系高等代数教研室 二零零二年五月 高等代数电子教案 第一章 多项式 第一节 数域 多项式是代数学中最基本的对象之一，它不但与高次方程的讨论有关，而且在进一步学习 代数以及其他数学分支时也会碰到。关于数的加、减、乘、除等运算的性质通常称为代数性 质。 定义 1 设 p 是由一些复数组成的集合，其中包括 0 与 1。如果 p 中任意两个数（这两个 数也可以相同）的和、差、积商（除数不为零）仍然是 p 中的数，那么 p 就称为一个数域。 如果数的集合 P 中任意两个数作某一运算的结果都仍然在 P 中，我们就说数集 P 对这个运 算封闭的

通常我们用Q表示有理数组成的集合，R表示全体实数组成的集合，C表示全体复数组成 的集合。 例1所有具有形式 a+b2 的数（其中a,b是任意有理数），构成一个数域。通常用g(瓦)来表示这个数域，显然数集QW) 包含0与1并且它对于加减法是封闭的。又 a+bW2e+d2)=(ac+2bd)+(ad+bch2,a,b,cd都是有理数，所以ac+2bd,ad+bc也 是有理数，即运算对乘法封闭。同理可得运算对除法封闭。 例2所有可以表成形式 +aπ+…+a,r b+bπ+…bnπm 的数组成一数域，其中n,m为任意非负整数，a,b,(=01,,匹j=0l,,m是整数 例3所有奇数组成的数集，对于乘法是封闭的，但对于加法、减法不是封闭的。√2的整 倍数的全体成一数集，它对于加、减法是封闭的，但对于乘除法不封闭。 数域的一个重要性质：所有的数域都包含有理数域作为它的一部分。 第二节一元多项式 定义2设n是一非负整数，形式表达式 anx"+an-1x+…+a。 (1) 其中a,a,…a,全属于数域P,称为系数在数域P中的一元多项式，或者简称为数域P中的 一元多项式。 在多项式(1)中，a,x称为1次项，a,称为1次项的系数。以后用fxgx,…或∫，g,…等 来表示多项式。 定义3如果在多项式x)与g(x)中，除去系数为零的项外，同次项的系数全相等，那 么f(x)与g)就称为相等，记为 f(x)=g(x) 系数全为零的多项式称为零多项式，记为0。 在(1)中，如果a。≠0，那么ax称为多项式(1)首项，an称为首项系数，n称为多项 式(1)的次数。零多项式是唯一不定义次数的多项式。 多项式fx)的次数记为fx). 设fy)=anx”+a-x++ao,g)=bx+b-x叫+…+b。 是数域P上的两个多项式。那么可以写成 fx)=∑a,x,gx)=∑b,x/ 在表示fx)与g气)的和时，如n2m,为了方便起见，在gc)中令bn=bn-1=…=b1=0

通常我们用 Q 表示有理数组成的集合， R 表示全体实数组成的集合， C 表示全体复数组成 的集合。 例 1 所有具有形式 a + b 2 的数（其中 a,b 是任意有理数），构成一个数域。通常用 Q( 2) 来表示这个数域，显然数集 Q( 2) 包含 0 与 1 并且它对于加减法是封闭的。又 (a + b 2)(c + d 2) = (ac + 2bd )+ (ad + bc) 2,a,b,c,d 都是有理数，所以 ac + 2bd,ad + bc 也 是有理数，即运算对乘法封闭。同理可得运算对除法封闭。 例 2 所有可以表成形式 m m n n b b b a a a       + + + + + 0 1 0 1 的数组成一数域，其中 n,m 为任意非负整数， a b (i n j m) i j , = 0,1,  , ; = 0,1,  , 是整数 例 3 所有奇数组成的数集，对于乘法是封闭的，但对于加法、减法不是封闭的。 2 的整 倍数的全体成一数集，它对于加、减法是封闭的，但对于乘除法不封闭。 数域的一个重要性质：所有的数域都包含有理数域作为它的一部分。 第二节 一元多项式 定义 2 设 n 是一非负整数，形式表达式 0 1 a x a 1 x a n n n n + + + − −  （1） 其中 a a an , , 0 1 全属于数域 P ，称为系数在数域 P 中的一元多项式，或者简称为数域 P 中的 一元多项式。 在多项式（1）中， i i a x 称为 i 次项， i a 称为 i 次项的系数。以后用 f (x), g(x),  或 f , g,  等 来表示多项式。 定义 3 如果在多项式 f (x) 与 g(x) 中，除去系数为零的项外，同次项的系数全相等，那 么 f (x) 与 g(x) 就称为相等，记为 f (x) = g(x) 系数全为零的多项式称为零多项式，记为 0。 在（1）中，如果  0, an 那么 n n a x 称为多项式（1）首项， n a 称为首项系数， n 称为多项 式（1）的次数。零多项式是唯一不定义次数的多项式。 多项式 f (x) 的次数记为 (f (x))。 设 ( ) , 0 1 f x a x a 1 x a n n n = n + + + − −  ( ) 0 1 g x b x b 1 x b m m m = m + + + − −  是数域 P 上的两个多项式。那么可以写成 ( )  ( )  = = = = m j j j n i i i f x a x g x b x 0 0 , 在表示 f (x)与 g(x)的和时，如 n  m, 为了方便起见，在 g(x)中令 0, bn = bn−1 == bm+1 =

那么f)与gx)的和为 )+g6)=a+b,k+a+bk-++a+6k+a+6)=∑a,+bk 而fx)与g(x)的积为 f(x)g(x)=a bxm+(a,b+ab xm++(abo+aob +aobo 其中s项的系数是 a,h+ab+tab+ab,=∑ab, 所以fx)gx)可写成 fs)=∑ab,k 显然，数域P上的两个多项式经过加、减、乘等运算后，所得结果仍然是数域P上的两 个多项式。 对于多项式的加减法，有af(x)士gx)smx(6(f(x儿g(x》 对于多项式的乘法，可以证明，如果fx)≠0，gx)≠0，那么fxgx)≠0，并且 U(x)g(x)=f(x》+(g(x),即多项式乘积的首项系数就等于因子首项系数的乘积。 和数的运算一样，多项式的运算也满足下面的一些规律： 1、加法交换律：fx)+gx)=gx)+fx) 2、加法结合律：(fx)+gx)+hx)=fx)+(gx)+x) 3、乘法交换律：fg()=gxf) 4、乘法结合律：（fxg(x)(x)=fxgx)x) 5、乘法对加法的分配律：fxg(x)+hx)=fxg(x)+fx)x) 6、乘法消去律：如果fxg(x)=fx)hx)且fx)≠0，那么gx)=x)。 定义4所有系数在数域P中的一元多项式的全体，称为数域P上的一元多项式环，记为 PxP称为P的系数。 第三节 整除的概念 这一节以后各节的讨论都是在某一固定的数域P上的多项式环Px中进行的，以后不再 重复说明了。 带余除法对于P]中任意两个多项式f(x)与gx),其中gx)≠O,一定有P]中的多项 式q(x))存在，使 f(x)=q(x)g(x)+r(x) (1) 成立，其中x)<(g(x》或者(x)=0,并且这样的q(x(x)是唯一确定的。 证明：(1)中qx)和(x)的存在性可以由上面所说的除法直接得出，用数学归纳法叙述。 如果fx)=0,取g)=)=0即可

那么 f (x) 与 g(x) 的和为 ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − + = + + − + − + + + + + = + n i i i i n n n n n n f x g x a b x a b x a b x a b a b x 0 1 1 0 0 1 1 1  而 f (x) 与 g(x) 的积为 ( ) ( ) ( ) ( ) 1 0 0 1 0 0 1 f x g x a b x a b 1 a 1b x a b a b x a b n m n m n m n m = n m + + + + + + + − − − +  其中 s 项的系数是  + = + − + + − + = i j s asb0 as 1b1  a1bs 1 a0bs aibj 所以 f (x) g(x) 可写成 ( ) ( ) s n m s i j s i j f x g x  a b x + = + =         = 0 显然，数域 P 上的两个多项式经过加、减、乘等运算后，所得结果仍然是数域 P 上的两 个多项式。 对于多项式的加减法，有 (f (x) g(x))  max((f (x)),(g(x))) 对于多项式的乘法，可以证明，如果 f (x)  0, g(x)  0, 那么 f (x)g(x)  0, 并且 (f (x)g(x)) = (f (x))+ (g(x)) ，即多项式乘积的首项系数就等于因子首项系数的乘积。 和数的运算一样，多项式的运算也满足下面的一些规律： 1、加法交换律： f (x)+ g(x) = g(x)+ f (x) 2、加法结合律： (f (x)+ g(x))+ h(x) = f (x)+ (g(x)+ h(x)) 3、乘法交换律： f (x)g(x) = g(x)f (x) 4、乘法结合律： (f (x)g(x))h(x) = f (x)(g(x)h(x)) 5、乘法对加法的分配律： f (x)(g(x)+ h(x)) = f (x)g(x)+ f (x)h(x) 6、乘法消去律：如果 f (x)g(x) = f (x)h(x) 且 f (x)  0, 那么 g(x) = h(x)。 定义 4 所有系数在数域 P 中的一元多项式的全体，称为数域 P 上的一元多项式环，记为 Px,P 称为 Px 的系数。 第三节 整除的概念 这一节以后各节的讨论都是在某一固定的数域 P 上的多项式环 Px 中进行的，以后不再 重复说明了。 带余除法 对于 Px 中任意两个多项式 f (x) 与 g(x) ，其中 g(x)  0, 一定有 Px 中的多项 式 q(x),r(x) 存在，使 f (x) = q(x)g(x)+ r(x) （1） 成立，其中 (r(x))  (g(x)) 或者 r(x) = 0, 并且这样的 q(x),r(x) 是唯一确定的。 证明：（1）中 q(x) 和 r(x) 的存在性可以由上面所说的除法直接得出，用数学归纳法叙述。 如果 f (x) = 0, 取 q(x) = r(x) = 0 即可

以下设fx)≠0。令fx)g(x)的次数分别为n,m,对fx)的次数n作数学归纳法。 当nr'(x)-r(x) 所以上式不可能成立。这就证明了g(x)=g(x),因此(x)=r'(x)。 带余除法中所得的q(x)通常称为g(x)除f(x)的商，r(x)称为g(x)除f(x)的余式 定义5数域P上的多项式g(x)称为整除f(x),如果有数域P上的多项式(x)使等式 f(x)=g(x)h(x) 成立。我们用g(xf()表示g(x)整除f(x),里g(x/(x)表丞g(x)不整隆fx) 当g(xf(x)时，g(x)称为f(x)的因式，f(x)称为g(x)的倍式。 当g(x)≠0时，带余除法给出了整除性的一个判别法。 定理1对于数域P上的任意两个多项式g(x),f(x),其中g(x)≠0，g(xf(x)的充分必 要条件是gx)除fx)的余式为零。 证明如果r(x)=0,那么f(x)=gx)h(x),即gx/x)。 反过来，如果g(xf(x),那么 f(x)=g(x)h(x)=g(x)h(x)+0

以下设 f (x)  0 。令 f (x), g(x) 的次数分别为 n,m ，对 f (x) 的次数 n 作数学归纳法。 当 n  m 时，显然取 q(x) = 0;r(x) = f (x), （1）式成立。 下面讨论 n  m 的情形。假设当次数小于 n 时， q(x),r(x) 的存在已证。现在看次数为 n 的情 形。 令 n n ax ,bx 分别是 f (x), g(x) 的首项，显然 b ax g(x) −1 n−m 与 f (x) 有相同的首相，因而多项式 ( ) ( ) ( ) 1 1 f x f x b ax g x − n−m = − 的次数小于 n 或为 0。对于后者，取 ( ) , ( ) 0 1 = = − − q x b ax r x n m ；对于前者，由归纳法假设， 对 ( ), ( ) 1 f x g x 有 ( ), ( ) 1 1 q x r x 存在使 ( ) ( ) ( ) ( ) 1 1 1 f x = q x g x + r x 其中 ( ( )) ( ( )) 1  r x   g x 或者 r(x) = 0 。于是 ( ) ( ( ) ) ( ) ( ) 1 1 1 f x q x b ax g x r x n m = + + − − 也就是说，有 ( ) ( ) , ( ) ( ) 1 1 1 q x q x b ax r x r x n m = + = − − 使 f (x) = q(x)g(x)+ r(x) 成立。由归纳法原理，对任意的 f (x), g(x)  0,q(x),r(x) 的存在性就证明了。 下面证明唯一性。设另有多项式 q (x),r (x) 使 f (x) = q (x)g(x)+ r (x) 其中 (r (x))  (g(x)) 或者 r (x) = 0 。于是 q(x)g(x)+ r(x) = q (x)g(x)+ r (x) 即 (q(x) − q (x))g(x) = r (x) − r(x) 如果 q(x)  q (x) ，又根据假设 g(x)  0, 那么 r (x) − r(x)  0, 且有 (q(x) − q (x)) + (g(x)) = (r (x) − r(x)) 但是 (g(x))  (r (x) − r(x)) 所以上式不可能成立。这就证明了 q(x) = q (x), 因此 r(x) = r (x) 。 带余除法中所得的 q(x) 通常称为 g(x) 除 f (x) 的商，r(x) 称为 g(x) 除 f (x) 的余式。 定义 5 数域 P 上的多项式 g(x) 称为整除 f (x) ，如果有数域 P 上的多项式 h(x) 使等式 f (x) = g(x)h(x) 成立。我们用 g(x) f (x) 表示 g(x) 整除 f (x) ，用 g(x) f (x) 表示 g(x) 不整除 f (x) 当 g(x) f (x) 时， g(x) 称为 f (x) 的因式， f (x) 称为 g(x) 的倍式。 当 g(x)  0 时，带余除法给出了整除性的一个判别法。 定理 1 对于数域 P 上的任意两个多项式 g(x) ， f (x) ，其中 g(x)  0, g(x) f (x) 的充分必 要条件是 g(x) 除 f (x) 的余式为零。 证明 如果 r(x) = 0 ，那么 f (x) = g(x)h(x) ，即 g(x) f (x) 。 反过来，如果 g(x) f (x) ，那么 f (x) = g(x)h(x) = g(x)h(x) + 0

即r(x)=0。 带余除法中g(x)必须不为零。但gxf(x)中，g(x)可以为零，这时 fx)=g(x)hx)=0.h(x)=0 当g(xf(x)时，如g(x)≠0，g(x)除f(x)所得的商q(x)有时也用 f(x) gx 来表示 下面介绍整除性的几个常用的性质： 1.如果gxf(x),fxg(x,那么fx)=cg(x),其中c为非零常数。 事实上，由fxg(x,有g(x)=h(x)fx,由g(xf()有fx)=gx)h(x)。于是 f(x)=h(x)h (x)f(x) 如果fx)为零，那么g(x)也为零，结论显然成立。如果f(x)≠0，那么消去f(x)就有 h,(x)h2(x)=1 从而ah(x)+ah,(x)=0。由此即得 ah,(x)=ah,(x)=0 也就是说h,(x)是一非零常数。 2.如果f(xg(x),gxx),那么x)x)(整除的传递性)。显然，由 g(x)=g(x)f(x).h(x)=h(x)g(x) 即得x)=(h,(xg(x)fx)。 3.如果fxg,(x),i=1,2,…,,那么 f(x4(x)g1(x)+42(x)g2(x)+…+4,(x)g,(x)2 其中w,(x)是数域P上任意的多项式。 通常4，(x)g1(x)+山2(x)g2(x)+…+4,(x)g,(x)称为多项式g1(x,g2(x,…,g,(x)的一个组合。 由以上性质可以看出，多项式f(x)与它的任一个非零常数倍gf(x)c≠0)有相同的因式， 也有相同倍式。因之，在多项式整除性的时论中，f(x)常常可以用f(x)来代替。 最后我们指出，两个多项式之间的整除关系不因为系数域的扩大而改变。也就是说，如果

即 r(x) = 0。 带余除法中 g(x) 必须不为零。但 g(x) f (x) 中， g(x) 可以为零，这时 f (x) = g(x) h(x) = 0  h(x) = 0 当 g(x) f (x) 时，如 g(x)  0 ， g(x) 除 f (x) 所得的商 q(x) 有时也用 ( ) ( ) g x f x 来表示。 下面介绍整除性的几个常用的性质： 1．如果 g(x) f (x)， f (x) g(x), 那么 f (x) = cg(x), 其中 c 为非零常数。 事实上，由 f (x) g(x), 有 ( ) ( ) ( ), 1 g x = h x f x 由 g(x) f (x) 有 ( ) ( ) ( ) 2 f x = g x h x 。于是 ( ) ( ) ( ) ( ) 1 2 f x = h x h x f x 如果 f (x) 为零，那么 g(x) 也为零，结论显然成立。如果 f (x)  0, 那么消去 f (x) 就有 h1 (x)h2 (x) =1 从而 (h1 (x))+ (h2 (x)) = 0 。由此即得 (h1 (x)) = (h2 (x)) = 0 也就是说 ( ) 2 h x 是一非零常数。 2．如果 f (x) g(x), g(x) h(x) ，那么 f (x) h(x) （整除的传递性）。显然，由 ( ) ( ) ( ), ( ) ( ) ( ) 1 1 g x = g x f x h x = h x g x 即得 ( ) ( ( ) ( )) ( ) 1 1 h x = h x g x f x 。 3．如果 f (x) g (x),i 1,2, ,r, i =  那么 ( )( ( ) ( ) ( ) ( ) ( ) ( )), 1 1 2 2 f x u x g x u x g x u x g x + ++ r r 其中 u (x) i 是数域 P 上任意的多项式。 通常 ( ) ( ) ( ) ( ) ( ) ( ) 1 1 2 2 u x g x u x g x u x g x + ++ r r 称为多项式 ( ), ( ), , ( ) 1 2 g x g x g x  r 的一个组合。 由以上性质可以看出，多项式 f (x) 与它的任一个非零常数倍 cf (x)(c  0) 有相同的因式， 也有相同倍式。因之，在多项式整除性的讨论中， f (x) 常常可以用 cf (x) 来代替。 最后我们指出，两个多项式之间的整除关系不因为系数域的扩大而改变。也就是说，如果

fx)、g(x)是P中两个多项式，P是包含P的一个较大的数域。当然f(x)、g(x)也可以 看成P中的多项式。从带余除法可以看出不论把f(x)、g(x)看成是P中或是P中的多 项式，用g(x)去除f(x)所得的商式及余式都是一样的。因此，如果P中g(x)不能整除f(x), 那么在x中，g(x)也不能整除∫(x) 第四节最大公因式 如果多项式(x)既是(x)的因式，又是g(x)的因式，那么p(x)就称为g(x)与f(x)的 个公因式。在公因式中占有特殊重要地位的是所谓最大公因式。 定义6设f(x),g(x)是Px中两个多项式。P]中多项式d(x)称为f(x),(x)的一个 最大公因式，如果它满足下面两个条件： 1)d(x)是f),g(x)的公因式： 2)f(x),g(x)的公因式全是d(x)的因式。 例如，对于任意多项式∫(x),f(x)就是(x)与0的一个最大公因式。特别地，根据定义， 两个零多项式的最大公因式就是0。 等大公因武的游在性的证明主要根据带余障法，关于带会除法我们脂出以下事实如果有 f(x)=q(x)g(x)+r(x) 成立，那么fx),g(x)和g(x),(x)有相同的公因式。事实上，如果(xg(x),p(x(x)。 这就是说，g(x),r(x)的公因式全是f(x),g(x)的公因式。反过来，如果(xg(x,p(xf(x) 那么p(x)一定整除它们的组合 r(x)=f(x)-q(x)g(x) 这就是说，p(x)是fx),g(x)的公因式。由此可见，如果g(x),r(x)有一个最大公因式d(x), 那么d(x)也就是f(x),g(x)的一个最大公因式。 定理2对于P中任意两个多项式f(x),g(x),在Px]中存在一个最大公因式d(x), 且d(x)可以表成f(x),g(x)的一个组合，即有P中多项式u(x,(x)使 d(x)=u(x)f(x)+v(x)g(x) (2)

f (x) 、 g(x) 是 Px 中两个多项式， P 是包含 P 的一个较大的数域。当然 f (x) 、 g(x) 也可以 看成 Px 中的多项式。从带余除法可以看出不论把 f (x) 、g(x) 看成是 Px 中或是 Px 中的多 项式，用 g(x) 去除 f (x) 所得的商式及余式都是一样的。因此，如果 Px 中 g(x) 不能整除 f (x) ， 那么在 Px 中， g(x) 也不能整除 f (x) 。 第四节 最大公因式 如果多项式 (x) 既是 f (x) 的因式，又是 g(x) 的因式，那么 (x) 就称为 g(x) 与 f (x) 的一 个公因式。在公因式中占有特殊重要地位的是所谓最大公因式。 定义 6 设 f (x) ，g(x) 是 Px 中两个多项式。 Px 中多项式 d (x) 称为 f (x) ，g(x) 的一个 最大公因式，如果它满足下面两个条件： 1） d (x) 是 f (x) ， g(x) 的公因式； 2） f (x) ， g(x) 的公因式全是 d (x) 的因式。 例如，对于任意多项式 f (x) ，f (x) 就是 f (x) 与 0 的一个最大公因式。特别地，根据定义， 两个零多项式的最大公因式就是 0。 最大公因式的存在性的证明主要根据带余除法，关于带余除法我们指出以下事实：如果有 等式 f (x) = q(x)g(x) + r(x) 成立，那么 f (x) ， g(x) 和 g(x)，r(x) 有相同的公因式。事实上，如果 (x) g(x),(x) f (x)。 这就是说， g(x)，r(x) 的公因式全是 f (x) ，g(x) 的公因式。反过来，如果 (x) g(x),(x) f (x) 那么 (x) 一定整除它们的组合 r(x) = f (x) − q(x)g(x) 这就是说， (x) 是 f (x) ，g(x) 的公因式。由此可见，如果 g(x) ，r(x) 有一个最大公因式 d (x) ， 那么 d (x) 也就是 f (x) ， g(x) 的一个最大公因式。 定理 2 对于 Px 中任意两个多项式 f (x) ， g(x) ，在 Px 中存在一个最大公因式 d (x) ， 且 d (x) 可以表成 f (x) ， g(x) 的一个组合，即有 Px 中多项式 u(x), v(x) 使 d(x) = u(x) f (x) + v(x)g(x) （2）

证明如果f(x),g(x)有一个为零，如g(x)=0,那么x)就是一个最大公因式，且 fx)=1·fx)+10 再看一般的情形。不妨设g(x)≠0。按带余除法，用g(x)除∫(x),得到商q,(x),余式(x): 如果(x)≠0，就再用r(x)除g(x),得到商(x),余式5()：如果(x)≠0，就再用() 除r(x),得到商q,(x)，余式(x):如此辗转相除下去，显然，所得余式的次数不断降低 即 g(x》>(x)0>,(x》>… 因此在有限次之后，必然有余式为零。于是我们有一串等式： f(x)=q(x)g(x)+r(x) g(x)=92(x)r(x)+5(x) t+0t+t00t+。0t0t0+++++0tt+0++00++ r-2(x)=g,(x)r(x)+r(x) … r-3(x)=q-(x)+r-(x) r-2(x)=9(xr-(x)+r.(x) r(x)=9(xr)r(x)+0 ,(x)与0的最大公因式是r,(x)。根据前面的说明，5(x)也就是r(x)与r-(x)的一个最大 公因式：同样的理由不，逐步推上去，r,(x)就是f(x),g(x)的一个最大公因式。 由上面等式容易得到等式 r(x)=u(x)f(x)+v(x)g(x) 这就是定理中的(2)式。 有最大公因式的定义不难看出，如果d,(x,d,(x)是f(x)与g(x)的两个最大公因式，那么 一定有d,(x4,(x)与d4,(xd,(x),也就是d,(x)=cd,(x,c≠0。这就是说，两个多项式的最大 公因式在可以相差一个非零常数倍的意义下是唯一确定的。两个不全为零的多项式的最大公 因式总是一个非零多项式。我们约定月 (fx),gx》 来表示首项系数是1的那个最大公因式。 定理证明中用来求最大公因式的方法通常称为辗转相除法

证明 如果 f (x) ， g(x) 有一个为零，如 g(x) = 0 ，那么 f (x) 就是一个最大公因式，且 f (x) = 1 f (x) +1 0 再看一般的情形。不妨设 g(x)  0 。按带余除法，用 g(x) 除 f (x) ，得到商 ( ) 1 q x ，余式 ( ) 1 r x ； 如果 r1 (x)  0 ，就再用 ( ) 1 r x 除 g(x) ，得到商 ( ) 2 q x ，余式 ( ) 2 r x ；如果 r2 (x)  0 ，就再用 ( ) 2 r x 除 ( ) 1 r x ，得到商 ( ) 3 q x ，余式 ( ) 3 r x ；如此辗转相除下去，显然，所得余式的次数不断降低， 即 (g(x))  (r1 (x)0  (r2 (x))  因此在有限次之后，必然有余式为零。于是我们有一串等式： ( ) ( ) ( ) ( ) 1 1 f x = q x g x + r x ( ) ( ) ( ) ( ) 2 1 2 g x = q x r x + r x ………………………………… ( ) ( ) ( ) ( ) 2 1 r x q x r x r x i− = i i− + i ………………………………… ( ) ( ) ( ) 3 1 1 r x q x r x s− = s− + s− ( ) ( ) ( ) ( ) 2 1 r x q x r x r x s− = s s− + s rs−1 (x) = qs+1 (x)rs (x) + 0 r (x) s 与 0 的最大公因式是 r (x) s 。根据前面的说明， r (x) s 也就是 r (x) s 与 ( ) 1 r x s− 的一个最大 公因式；同样的理由不，逐步推上去， r (x) s 就是 f (x) ， g(x) 的一个最大公因式。 由上面等式容易得到等式 r (x) u(x) f (x) v(x)g(x) s = + 这就是定理中的（2）式。 有最大公因式的定义不难看出，如果 ( ), ( ) 1 2 d x d x 是 f (x) 与 g(x) 的两个最大公因式，那么 一定有 ( ) ( ) 1 2 d x d x 与 ( ) ( ) 2 1 d x d x ，也就是 d1 (x) = cd2 (x),c  0 。这就是说，两个多项式的最大 公因式在可以相差一个非零常数倍的意义下是唯一确定的。两个不全为零的多项式的最大公 因式总是一个非零多项式。我们约定用 ( f (x), g(x)) 来表示首项系数是 1 的那个最大公因式。 定理证明中用来求最大公因式的方法通常称为辗转相除法

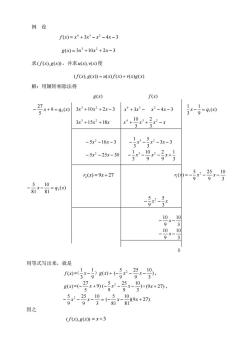
例设 f(x)=x+3x3-x2-4x-3 g(x)=3x3+10x2+2x-3 求(fx),g(x),并求u(x,Mx)使 (f(x),g(x》=(x)f(x)+(x)g(x) 解：用辗转相除法得 g(x) f(x) 27 x+9=9) 3x3+10x2+2x-3x+3x3-x2-4x-3 3x3+15x2+18x +9+号-x 3 -5.x2-16x-3 r--3-3 -5x2-25x-30 9 5(x)=9x+27 --9 -2-x 0 用等式写出来，就是 --号g+3--9. 8=-2+9-x-9-9x+2 因之 (fxgx》=x+3

例 设 ( ) 3 4 3 4 3 2 f x = x + x − x − x − ( ) 3 10 2 3 3 2 g x = x + x + x − 求 ( f (x), g(x)) ，并求 u(x), v(x) 使 ( f (x), g(x)) = u(x) f (x) + v(x)g(x) 解：用辗转相除法得 g(x) f (x) 9 ( ) 5 27 2 − x + = q x 3 10 2 3 3 2 x + x + x − 3 4 3 4 3 2 x + x − x − x − ( ) 9 1 3 1 1 x − = q x 3x 15x 18x 3 2 + + x + x + x − x 4 3 2 3 2 3 10 5 16 3 2 − x − x − 3 3 3 5 3 1 3 2 − x − x − x − 5 25 30 2 − x − x − 3 1 9 2 9 10 3 1 3 2 − x − x − x + r2 (x) = 9x + 27 3 10 9 25 9 5 ( ) 2 r1 x = − x − x − ( ) 81 10 81 5 3 − x − = q x x x 3 5 9 5 2 − − 3 10 9 10 − x − 3 10 9 10 − x − 0 用等式写出来，就是 f (x) = − ( ) + 9 1 3 1 （ x ）g x ) 3 10 9 25 9 5 ( 2 − x − x − ， g(x) = 9) 5 27 (− x + ) 3 10 9 25 9 5 ( 2 − x − x − + (9x + 27) ， − − − = 3 10 9 25 9 5 2 x x )(9 27). 81 10 81 5 (− x − x + 因之 ( f (x), g(x)) = x + 3

而 9x+2-8-2+9--9 =g-马+[a-(令g 号-r+1-g--a =号-+号+ 于是 auwω得x-ym+(传+号t国 定义7Px中两个多项式f(x),g(x)称为互素的，如果(f(x),g(x》=1。 显然，如果两个多项式互素，那么它们除去零次多项式外没有其他的公因式，反之亦然。 定理3P中两个多项式fx),gx)互素的充分必要条件是有P)中的多项式(x),(x)使 u(x)f(x)+v(x)g(x)=1 证明必要条件是定理2的直接推论。 现在设有(x),r(x)使 u(x)f(x)+v(x)g(x)=1 而o(x)是f(x)与g(x)的一个最大公因式。于是p(xf(x),p(xg(x),从而p(x儿，即f(x), g(x)互素。 定理4如果(f(x),g(x》=l,且fxg(x)hx),那么f(xh)。 证明由((x),g(x》=1可知，有(x),(x)使 4(x)f(x)+v(x)gr)=1, 等式两边乘h(x),得 u(x)f(x)h(x)+v(x)g(x)h(x)=h(x) 因为f(xg(x)hx),所以f（x)整除等式左端，从而 f(x)h(x). 推论如果(xg(x,f(xg(x),且(f(x,(x》=1,那么f(x)f(xg(x)

而 (9x + 27) = g(x) − 9) 5 27 (− x + ) 3 10 9 25 9 5 ( 2 − x − x − = g(x) − 9) 5 27 (− x +  f (x)- ( )  9 1 3 1 （ x − ）g x = ( ) 9 1 3 1 9 5 27 9) ( ) 1 5 27 ( x f x x x g x              −      − + − − = ( ) 5 18 5 9 9) ( ) 5 27 ( 2 x f x x xg x      − + − + 于是 ( f (x), g(x)) = ( ) 5 2 5 1 1 ( ) 5 3 2 x f x x xg x       + − +      − 定义 7 Px 中两个多项式 f (x) ， g(x) 称为互素的，如果 ( f (x), g(x)) =1。 显然，如果两个多项式互素，那么它们除去零次多项式外没有其他的公因式，反之亦然。 定理 3 Px 中两个多项式 f (x) ，g(x) 互素的充分必要条件是有 Px 中的多项式 u(x), v(x) 使 u(x) f (x) + v(x)g(x) = 1 证明 必要条件是定理 2 的直接推论。 现在设有 u(x), v(x) 使 u(x) f (x) + v(x)g(x) = 1 而 (x) 是 f (x) 与 g(x) 的一个最大公因式。于是 (x) f (x),(x) g(x), 从而 (x)1, 即 f (x) ， g(x) 互素。 定理 4 如果 ( f (x), g(x)) =1，且 f (x) g(x)h(x), 那么 f (x) h(x)。 证明 由 ( f (x), g(x)) =1 可知，有 u(x), v(x) 使 u(x) f (x) + v(x)g(x) = 1， 等式两边乘 h(x), 得 u(x) f (x)h(x) + v(x)g(x)h(x) = h(x) 因为 f (x) g(x)h(x), 所以 f (x) 整除等式左端，从而 f (x) h(x). 推论 如果 ( ) ( ), 1 f x g x ( ) ( ) 2 f x g x ，且 ( f 1 (x), f 2 (x)) =1 ，那么 ( ) ( ) ( ) 1 2 f x f x g x

证明由(x)g(x)有 g(x)=f(x)h(x). 因为f(xf(x)h(x),且(f(x,f(x》=1,所以根据定理4，有(xh,(x),即 h(x)=f(x)h(x) 代入上式即得 g(x)=f(x)f(x)h(x) 这就是说， f(x)f(xg(x)。 在上面，最大公因式与互素的概念，都是对两个多项式定义的。事实上，对于任意多个多项 式(x),(x,,f,(x(s之2)也同样可以定义最大公因式，dx)称为 f(x),,(x,,∫.(xs≥2)的一个最大公因式，如果d(x)具有下面的性质： 1)dx/(xi=1,2,…s 2)如果xf(x),i=1,2,…,s,那么p(x)d(x)。 我们仍用符号(x),f(x.,f(x)来表示首项系数为1的最大公因式，且存在 4,(x,i=1,2…,s使 4(x)f(x)+42(x)f2(x)+…+4,(x)f(x)=f(x),f2(x,…,f(x) 如果x,2(x,…,(x)=1,那么f(x(x…,(x)就称为互素的。 第五节因式分解定理 选定一个数域P作为系数域，考虑数域P上的多项式环P]中多项式的因式分解。 定义8数域P上次数≥1的多项式(x)称为数域P上的不可约多项式，如果它不能表成数 域P上的两个次数比(x)低的多项式的乘积。 按照定义，一次多项式总是不可约多项式。 如上面指出的，x2+2是实数域上的不可约多项式，但是它在复数域上可以分解成两个一次 多项式的乘积，因而不是不可约多项式。这说明了，一个多项式是否不可约是依赖与系数域 的。 显然，不可约多项式p(x)的因式只有非零常数和它自身的非零常数倍p(xc≠0)这两种

证明 由 ( ) ( ) 1 f x g x 有 ( ) ( ) ( ) 1 1 g x = f x h x 。 因为 ( ) ( ) ( ) 2 1 1 f x f x h x ，且 ( f 1 (x), f 2 (x)) =1 ，所以根据定理 4，有 ( ) ( ) 2 1 f x h x ，即 ( ) ( ) ( ) 1 2 2 h x = f x h x 代入上式即得 ( ) ( ) ( ) ( ) 1 2 2 g x = f x f x h x 这就是说， ( ) ( ) ( ) 1 2 f x f x g x 。 在上面，最大公因式与互素的概念，都是对两个多项式定义的。事实上，对于任意多个多项 式 ( ), ( ), , ( )( 2) f 1 x f 2 x  f s x s  也 同 样 可 以 定 义 最 大 公 因 式 ， d (x) 称 为 ( ), ( ), , ( )( 2) f 1 x f 2 x  f s x s  的一个最大公因式，如果 d (x) 具有下面的性质： 1） d x f x i s i ( ) ( ), =1,2,  , 2）如果 (x) f (x),i 1,2, ,s,  i =  那么 (x) d(x)。 我们仍用符号 ( ( ), ( ), , ( )) 1 2 f x f x f x  s 来表示首项系数为 1 的最大公因式，且存在 u x i s i ( ), =1,2,  , 使 u1 (x) f 1 (x) + u2 (x) f 2 (x) ++ us (x) f s (x) = ( ( ), ( ), , ( )) 1 2 f x f x f x  s 如果 ( ( ), ( ), , ( )) 1 2 f x f x f x  s =1，那么 ( ), ( ), , ( ) 1 2 f x f x f x  s 就称为互素的。 第五节 因式分解定理 选定一个数域 P 作为系数域，考虑数域 P 上的多项式环 Px 中多项式的因式分解。 定义 8 数域 P 上次数  1 的多项式 p(x) 称为数域 P 上的不可约多项式，如果它不能表成数 域 P 上的两个次数比 p(x) 低的多项式的乘积。 按照定义，一次多项式总是不可约多项式。 如上面指出的， 2 2 x + 是实数域上的不可约多项式，但是它在复数域上可以分解成两个一次 多项式的乘积，因而不是不可约多项式。这说明了，一个多项式是否不可约是依赖与系数域 的。 显然，不可约多项式 p(x) 的 因式只有非零常数和它自身的非零常数倍 cp(x)(c  0) 这两种