中国科学技术大学：《数字几何处理 Digital Geometry Processing》课程教学资源（课件讲义）04 Mesh Parameterizations

Mesh Parameterizations Xiao-Ming Fu

Mesh Parameterizations Xiao-Ming Fu

Outline 。Definition Tutte's barycentric mapping Least squares conformal maps(LSCM,ASAP) Angle-Based Flattening (ABF) ·ABF++,LABF As-rigid-as-possible (ARAP) ·Simplex Assembly

Outline • Definition • Tutte’s barycentric mapping • Least squares conformal maps(LSCM, ASAP) • Angle-Based Flattening (ABF) • ABF++, LABF • As-rigid-as-possible (ARAP) • Simplex Assembly

Definition °A function that puts input surface in one-to- one correspondence with a 2D domain. Parameterization of a Triangulated Surface all (ui,vi)coordinates associated with each vertex vi (xi,yi,Zi ) 3D 2D

Definition • A function that puts input surface in one -to - one correspondence with a 2D domain. • Parameterization of a Triangulated Surface • all (𝑢𝑖, 𝑣𝑖) coordinates associated with each vertex 𝒗 𝑖 = 𝑥 𝑖 , 𝑦 𝑖 , 𝑧 𝑖 𝑇 3D 2 D

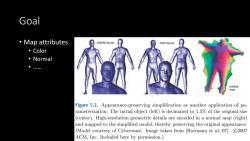
Goal ·ap attributes 290000 facets 3500 facets 。Color 。Normal map Figure 5.2.Appearance-preserving simplification as another application of pa- rameterization:The initial object (left)is decimated to 1.5%of the original size (center).High-resolution geometric details are encoded in a normal map (right) and mapped to the simplified model,thereby preserving the original appearance. (Model courtesy of Cyberware.Image taken from [Hormann et al.07].C2007 ACM,Inc.Included here by permission.)

Goal • Map attributes • Color • Normal • ……

Constraints ·Bijective The image of the surface in parameter space does not self-intersect. The intersection of any two triangles in parameter space is either a common edge,a common vertex,or empty

Constraints • Bijective • The image of the surface in parameter space does not self-intersect. • The intersection of any two triangles in parameter space is either a common edge, a common vertex, or empty

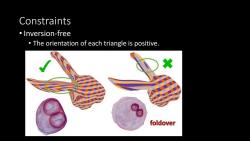
Constraints 。Inversion-free The orientation of each triangle is positive. 然 foldover

Constraints • Inversion-free • The orientation of each triangle is positive

Constraints ·Locally injective The orientation of each triangle is positive det>0. For boundary vertex,the mapping is locally bijective-> 0()>2π. 0()>2π θ()<2π

Constraints • Locally injective • The orientation of each triangle is positive → det𝐽 > 0. • For boundary vertex, the mapping is locally bijective → 𝜃 𝒗 > 2𝜋. 𝜃 𝒗 2𝜋 𝒗

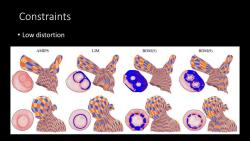
Constraints 。Low distortion AMIPS LIM BDM(5) BDM(9)

Constraints • Low distortion

Outline 。Definition Tutte's barycentric mapping Least squares conformal maps(LSCM,ASAP) Angle-Based Flattening (ABF) ·ABF+,LABF As-rigid-as-possible (ARAP) 。Simplex Assembly

Outline • Definition • Tutte’s barycentric mapping • Least squares conformal maps(LSCM, ASAP) • Angle-Based Flattening (ABF) • ABF++, LABF • As-rigid-as-possible (ARAP) • Simplex Assembly

Barycentric Mapping One of the most widely used methods. Given a triangulated surface homeomorphic to a disk,if the (u,v)coordinates at the boundary vertices lie on a convex polygon in order,and if the coordinates of the internal vertices are a convex combination of their neighbors,then the (u,v)coordinates form a valid parameterization (without self-intersections,bijective)

Barycentric Mapping • One of the most widely used methods. Given a triangulated surface homeomorphic to a disk, if the (𝑢, 𝑣) coordinates at the boundary vertices lie on a convex polygon in order, and if the coordinates of the internal vertices are a convex combination of their neighbors, then the (𝑢, 𝑣) coordinates form a valid parameterization (without self-intersections, bijective)