同济大学：《高等数学 Advanced Mathematics》课程教学资源（高数D，PPT课件）极限 Limits & Continuity

Chapter Two Limits Continuity

Chapter Two Limits & Continuity

Enter Calculus World ●Ve have known“Function” o This is the tool for us enter the Calculus World ●The first adventure is“Limit” o Limits is the soul of Calculus as well as "Advanced Mathematics"!

Enter Calculus World ⚫We have known “Function” ⚫This is the tool for us enter the Calculus World ⚫The first adventure is “Limit” ⚫Limits is the soul of Calculus as well as “Advanced Mathematics”!

Ancient Limit Thought ● Zhuangzi(庄子，369-286B.C) in《天下》said: ○一尺之锤，日取其半，万世不竭。 o Chinese ancient mathematician Liu Hui(刘徽)in263a.c.said in《九章算术》 ○“割之弥细，所失弥小.割之又割， 以至于不可割，则与圆周合体，而无 所失矣

Ancient Limit Thought ⚫ Zhuangzi （庄子,369-286 B.C） in《天下》said: 一尺之锤，日取其半，万世不竭。 ⚫ Chinese ancient mathematician Liu Hui （刘徽） in 263 a.c. said in《九章算术》 : “割之弥细，所失弥小. 割之又割， 以至于不可割，则与圆周合体，而无 所失矣

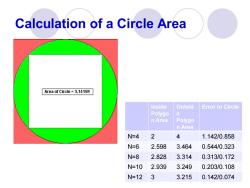
Calculation of a Circle Area Area of Circle =3.14159 Inside Outsid Error to Circle Polygo e n Area Polygo n Area N=4 2 4 1.142/0.858 N=6 2.598 3.464 0.544/0.323 N=8 2.828 3.314 0.313/0.172 N=10 2.939 3.249 0.203/0.108 N=123 3.215 0.142/0.074

Inside Polygo n Area Outsid e Polygo n Area Error to Circle N=4 2 4 1.142/0.858 N=6 2.598 3.464 0.544/0.323 N=8 2.828 3.314 0.313/0.172 N=10 2.939 3.249 0.203/0.108 N=12 3 3.215 0.142/0.074 Calculation of a Circle Area

Zeno of Elea (490-430 BC) paradoxes- O Achilles and the Tortoise OA is in a footrace with a slow T by 10*its speed. OA allows T a head start of 100 meters. OAfter A run 100 m,to T start point,meanwhile,T run 10 m. OA then run 10 m,and T has advanced farther; OA need more time to reach 3rd point,while T moves ahead. O Thus,whenever A reaches somewhere T has been,he still has farther to go.Therefore,as there are an infinite number of points A must reach where T has already been,he never overtake T

Zeno of Elea (490–430 BC) paradoxes- ⚫ Achilles and the Tortoise ： A is in a footrace with a slow T by 10* its speed. A allows T a head start of 100 meters. After A run 100 m, to T start point, meanwhile, T run 10 m. A then run 10 m, and T has advanced farther; A need more time to reach 3rd point, while T moves ahead.  Thus, whenever A reaches somewhere T has been, he still has farther to go. Therefore, as there are an infinite number of points A must reach where T has already been, he never overtake T

Some Examples for Limit ●Value of a function ●Area Problem OGiven a function f;find the area between the graph of fand an interval on the x-axis ●Tangent Line Problem OGive a function f;and a point on its graph,find an equation of the line that is tangent to the graph at the point

Some Examples for Limit ⚫Value of a function ⚫Area Problem Given a function f, find the area between the graph of f and an interval on the x-axis ⚫Tangent Line Problem Give a function f, and a point on its graph, find an equation of the line that is tangent to the graph at the point

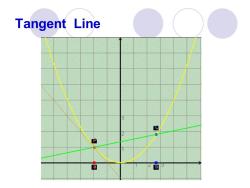
Tangent Line

Tangent Line

Limit (An Informal View) If the value of f(x)can be made as close as we like to L by taking values of x sufficiently to a(not equal to a),then we write lim f(x)=L X->0 ●Read as: 0rf(x)>L,asx→a “the limit of f(x)as x approaches a is L.” ●Equivalently 1im(f(x)-L)=0

Limit (An Informal View) ⚫If the value of f (x) can be made as close as we like to L by taking values of x sufficiently to a (not equal to a), then we write ⚫Read as: “the limit of f (x) as x approaches a is L.” ⚫Equivalently lim ( ) ( ) , x a f x L or f x L as x a → = → → lim ( ) 0 ( ) x a f x L → − =

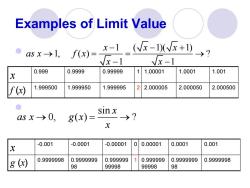
Examples of Limit Value x-1 f(x)= (N-1)(x+1) 4Sx→1， -1 0.999 0.9999 0.99999 1 1.00001 1.0001 1.001 X f(x) 1.999500 1.999950 1.999995 2 2.000005 2.000050 2.000500 Sinx asx→0， 8(x)= >? x -0.001 -0.0001 -0.00001 0/ 0.00001 0.0001 0.001 (x) 0.9999998 0.999999 1 g 0.9999999 0.999999 0.9999999 0.9999998 98 99998 99998 98

Examples of Limit Value ⚫ ⚫ 1 ( 1)( 1) 1, ( ) ? 1 1 x x x as x f x x x − − + → = = → − − x 0.999 0.9999 0.99999 1 1.00001 1.0001 1.001 f (x) 1.999500 1.999950 1.999995 2 2.000005 2.000050 2.000500 sin 0, ( ) ? x as x g x x → = → x -0.001 -0.0001 -0.00001 0 0.00001 0.0001 0.001 g (x) 0.9999998 0.9999999 98 0.999999 99998 1 0.999999 99998 0.9999999 98 0.9999998

Example of No Limit Value asx→0，f(x)=sin π x πk f(x) ±2 ±π/2 ±1 士1 士π 0 ±2/3 ±T/2 ±1 ±10/100 士10 0 ±10/105 ±(10+1/2)π ±1 ±10/1000 ±100元 0 ±10/1005 ±(100+1/2) ±1 ±10/10000 士1000元 0 ±10/10005 ±(1000+1/2)π ±1 ±10/100000 +10000元 0

Example of No Limit Value ⚫ ⚫ as x f x 0, ( ) sin ? x    → = →     x π/x f(x) ±2 ±π/2 ±1 ±1 ±π 0 ±2/3 ±π/2 ±1 ±10/100 ±10π 0 ±10/105 ±(10+1/2)π ±1 ±10/1000 ±100π 0 ±10/1005 ±(100+1/2)π ±1 ±10/10000 ±1000π 0 ±10/10005 ±(1000+1/2)π ±1 ±10/100000 ±10000π 0