广东工业大学：《机器学习》课程教学资源（课件讲义）第15讲 无监督学习——降维深度学习可视化（Neighbor Embedding，LLE T-SNE）

Unsupervised Learning: Neighbor Embedding

Unsupervised Learning: Neighbor Embedding

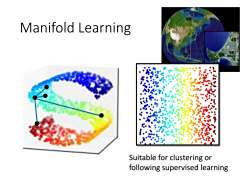
Manifold Learning Suitable for clustering or following supervised learning

Manifold Learning Suitable for clustering or following supervised learning

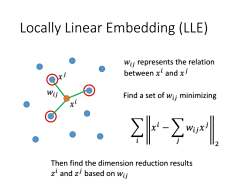
Locally Linear Embedding (LLE) Wij represents the relation between xl and x Find a set of wii minimizing k-yl Then find the dimension reduction results zi and z based on wij

Locally Linear Embedding (LLE) 𝑥 𝑖 𝑥 𝑗 𝑤𝑖𝑗 𝑤𝑖𝑗 represents the relation between 𝑥 𝑖 and 𝑥 𝑗 Find a set of 𝑤𝑖𝑗 minimizing ෍ 𝑖 𝑥 𝑖 − ෍ 𝑗 𝑤𝑖𝑗𝑥 𝑗 2 Then find the dimension reduction results 𝑧 𝑖 and 𝑧 𝑗 based on 𝑤𝑖𝑗

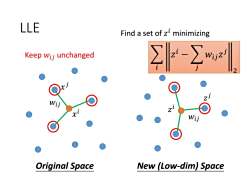
LLE Find a set of z minimizing Keep wij unchanged -Σ Wi Original Space New (Low-dim)Space

LLE 𝑥 𝑖 𝑥 𝑗 𝑤𝑖𝑗 𝑤𝑖𝑗 𝑧 𝑗 𝑧 𝑖 Original Space New (Low-dim) Space Find a set of 𝑧 𝑖 minimizing Keep 𝑤𝑖𝑗 unchanged ෍ 𝑖 𝑧 𝑖 − ෍ 𝑗 𝑤𝑖𝑗𝑧 𝑗 2

LLE xt,xi Wij 在地領為連理校 在天顧作出墨焉 Wij Source of image: http://feetsprint.blogspot.tw/2016 /02/blog-post_29.html

LLE Source of image: http://feetsprint.blogspot.tw/2016 /02/blog-post_29.html 𝑧 𝑖 ,𝑧 𝑗 𝑤𝑖𝑗 𝑤𝑖𝑗 𝑥 𝑖 ,𝑥 𝑗

LLE Lawrence K.Saul,Sam T.Roweis,"Think Globally,Fit Locally: Unsupervised Learning of Low Dimensional Manifolds",JMLR,2013 K=5 K=6 K= K=10 12 16 18 K=20 K=30 K=40 K=60

LLE Lawrence K. Saul, Sam T. Roweis, “Think Globally, Fit Locally: Unsupervised Learning of Low Dimensional Manifolds”, JMLR, 2013

Laplacian Eigenmaps Graph-based approach Distance defined by graph approximate the distance on manifold Construct the data points as a graph

Laplacian Eigenmaps • Graph-based approach Construct the data points as a graph Distance defined by graph approximate the distance on manifold

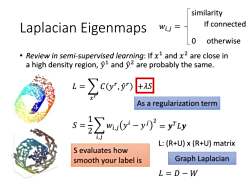
similarity Laplacian Eigenmaps Wi,j= If connected 0 otherwise Review in semi-supervised learning:If x1 and x2 are close in a high density region,1 and 2 are probably the same. t=∑co )+ As a regularization term s=2∑0-'=yy L:(R+U)x(R+U)matrix S evaluates how smooth your label is Graph Laplacian L=D-W

Laplacian Eigenmaps • Review in semi-supervised learning: If 𝑥 1 and 𝑥 2 are close in a high density region, 𝑦 ො 1 and 𝑦 ො 2 are probably the same. 𝐿 = ෍ 𝑥 𝑟 𝐶 𝑦 𝑟 , 𝑦 ො 𝑟 +𝜆𝑆 As a regularization term = 𝒚 𝑇 𝑆 = 𝐿𝒚 1 2 ෍ 𝑖,𝑗 𝑤𝑖,𝑗 𝑦 𝑖 − 𝑦 𝑗 2 L: (R+U) x (R+U) matrix Graph Laplacian 𝐿 = 𝐷 − 𝑊 S evaluates how smooth your label is 𝑤𝑖,𝑗 = 0 similarity If connected otherwise

Laplacian Eigenmaps Dimension Reduction:If x1 and x2 are close in a high density region,z1 and z2 are close to each other. s=∑ue-z Any problem?How about zi=z=0? Giving some constraints to z: If the dim of z is M,Span(z1,z2,...N)=RM Spectral clustering:clustering on z Belkin,M.,Niyogi,P.Laplacian eigenmaps and spectral techniques for embedding and clustering.Advances in neural information processing systems.2002

Laplacian Eigenmaps • Dimension Reduction: If 𝑥 1 and 𝑥 2 are close in a high density region, 𝑧 1 and 𝑧 2 are close to each other. 𝑆 = 1 2 ෍ 𝑖,𝑗 𝑤𝑖,𝑗 𝑧 𝑖 − 𝑧 𝑗 2 Spectral clustering: clustering on z Any problem? How about 𝑧 𝑖 = 𝑧 𝑗 = 𝟎? Giving some constraints to z: If the dim of z is M, Span{z1 , z2 , … z N} = RM Belkin, M., Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Advances in neural information processing systems . 2002

T-distributed Stochastic Neighbor Embedding (t-SNE) Problem of the previous approaches Similar data are close,but different data may collapse LLE on MNIST LLE on COIL-20

T-distributed Stochastic Neighbor Embedding (t-SNE) • Problem of the previous approaches • Similar data are close, but different data may collapse LLE on MNIST LLE on COIL-20