山东理工大学：《机械优化设计》课程教学课件（PPT讲稿）第五章 无约束优化方法

第四章无约束优化方法 第一节 概述 从第一章列举的机械设计问题，大多数实际问题是约 束优化问题。 约束优化问题的求解——转化为一系列的无约束优化问 题实现的。 因此，无约束优化问题的解法是优化设计方法的基本组 成部分，也是优化方法的基础。 ( ) * 无约束优化问题的极值条件  = f x 0

第四章无约束优化方法 第一节 概述 从第一章列举的机械设计问题，大多数实际问题是约 束优化问题。 约束优化问题的求解——转化为一系列的无约束优化问 题实现的。 因此，无约束优化问题的解法是优化设计方法的基本组 成部分，也是优化方法的基础。 ( ) * 无约束优化问题的极值条件  = f x 0

解析法 数值法 数学模型复杂时不便求解 可以处理复杂函数及没有数学表达式 的优化设计问题 k k k 1 k x x a d + = + 搜索方向问题是无约束优化方法的关键。 各种无约束优化方法的区别：确定搜索方向的方法不同。 无约束优化方法分类 利用目标函数的一阶或二阶导数 利用目标函数值 （最速下降法、共轭梯度法、牛顿法） （坐标轮换法、鲍威尔等）

解析法 数值法 数学模型复杂时不便求解 可以处理复杂函数及没有数学表达式 的优化设计问题 k k k 1 k x x a d + = + 搜索方向问题是无约束优化方法的关键。 各种无约束优化方法的区别：确定搜索方向的方法不同。 无约束优化方法分类 利用目标函数的一阶或二阶导数 利用目标函数值 （最速下降法、共轭梯度法、牛顿法） （坐标轮换法、鲍威尔等）

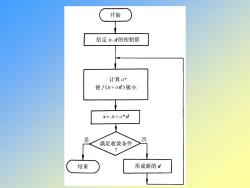
开始 给定x、d的初始值 计算a* 使f(x+ad)极小 x-x+a*d 是 满足收敛条件 否 结束 形成新的d

第二节 最速下降法 优化设计追求目标函数值最小，若搜索方向取该点的负梯度 方向，使函数值在该点附近的范围内下降最快。 按此规律不断走步，形成以下迭代算法： ( ) k k k 1 k x x a f x + = −  以负梯度方向为搜索方向，所以称最速下降法或梯度法。 搜索方向确定为负梯度方向，还需确定步长因子 k a 即求一维搜索的最佳步长，既有 ( ) ( ) ( ) ( ) 1 min min k k k k k k k f x f x a f x f x a f x     + = −  = −  =        

第二节 最速下降法 优化设计追求目标函数值最小，若搜索方向取该点的负梯度 方向，使函数值在该点附近的范围内下降最快。 按此规律不断走步，形成以下迭代算法： ( ) k k k 1 k x x a f x + = −  以负梯度方向为搜索方向，所以称最速下降法或梯度法。 搜索方向确定为负梯度方向，还需确定步长因子 k a 即求一维搜索的最佳步长，既有 ( ) ( ) ( ) ( ) 1 min min k k k k k k k f x f x a f x f x a f x     + = −  = −  =        

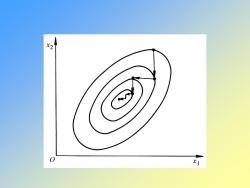
( )  ( )  ( ) 0 T k k k k   = −  −   = f x a f x f x     ( ) ( ) 1 0 T k k f x f x +     =   ( ) 1 0 T k k d d + = 由此可知，在最速下降法中，相邻两个迭代点上的函数 梯度相互垂直。而搜索方向就是负梯度方向，因此相邻 两个搜索方向互相垂直

( )  ( )  ( ) 0 T k k k k   = −  −   = f x a f x f x     ( ) ( ) 1 0 T k k f x f x +     =   ( ) 1 0 T k k d d + = 由此可知，在最速下降法中，相邻两个迭代点上的函数 梯度相互垂直。而搜索方向就是负梯度方向，因此相邻 两个搜索方向互相垂直

2

例4-1 求目标函数 ( ) 2 2 1 2 f x x x = + 25 的极小点

例4-1 求目标函数 ( ) 2 2 1 2 f x x x = + 25 的极小点

开始 给定x0、e k0 dk-vf (xk) xk+l←xk+adk k←k+1 ag:minf(xk+adk) 是 xk+1-xk<6? 否 x*←xk+l 结束

第三节牛顿型方法 在第三章中，我们已经讨论了一维搜索的牛顿方法。 得出一维情况下的牛顿迭代公式 ( ) ( ) 1 k k k k f x x x f x +  = −  对于多元函数，在 k x 泰勒展开，得 f x x ( )  ( ) ( ) ( ) ( ) ( ) ( )( ) 1 2 2 T T k k k k k k = +  − + −  − f x f x x x x x f x x x 设 k 1 x + 为函数的极小点，根据极值的必要条件

第三节牛顿型方法 在第三章中，我们已经讨论了一维搜索的牛顿方法。 得出一维情况下的牛顿迭代公式 ( ) ( ) 1 k k k k f x x x f x +  = −  对于多元函数，在 k x 泰勒展开，得 f x x ( )  ( ) ( ) ( ) ( ) ( ) ( )( ) 1 2 2 T T k k k k k k = +  − + −  − f x f x x x x x f x x x 设 k 1 x + 为函数的极小点，根据极值的必要条件

( ) 1 0 k  x +  = ( ) ( )( ) 2 1 0 k k k k f x f x x x +  +  − = ( ) ( ) 1 k k k k 1 2 x x f x f x − + = −       这是多元函数求极值的牛顿法迭代公式。 例4-2 用牛顿法求 ( ) 2 2 1 2 f x x x = + 25 的极小值。 对牛顿法进行改进，提出“阻尼牛顿法” ( ) ( ) 1 k k k k 1 2 k x x f x f x  − + = −       ( ) 1 min k k k k k k f x f x a d f x ad  + = + = +        

( ) 1 0 k  x +  = ( ) ( )( ) 2 1 0 k k k k f x f x x x +  +  − = ( ) ( ) 1 k k k k 1 2 x x f x f x − + = −       这是多元函数求极值的牛顿法迭代公式。 例4-2 用牛顿法求 ( ) 2 2 1 2 f x x x = + 25 的极小值。 对牛顿法进行改进，提出“阻尼牛顿法” ( ) ( ) 1 k k k k 1 2 k x x f x f x  − + = −       ( ) 1 min k k k k k k f x f x a d f x ad  + = + = +        