江西农业大学：《数字逻辑》课程教学资源（PPT讲稿）第三章 布尔代数与逻辑函数化简——3.3 卡诺图 3.3.4 逻辑函数的卡诺图表示法

逻辑函数的卡诺图表示法 一、化成最小项表达式后填写卡诺图 【例】填写函数的卡诺图，F的表达式如下 F=∑1,7,12)=m1+m,+m2=A·B.C.D+ABCD+ABC.D 解：由表达式中的m知该函数为四变量函数所以需要四变量卡诺图观 察得知表达式已是最小项表达式只需将每一个最小项填入卡诺图即可 在ABCD对应0O01的方格里填1即表示最小项即M,=ABCD 同样在0111和1100的方格中填1即得下图（其余填0，通常可省略） CD 00 01 11 10 AB 00 01 1 11 1 10

逻辑函数的卡诺图表示法 一、化成最小项表达式后填写卡诺图 【例】 填写函数F的卡诺图，F 的表达式如下 F = (1,7,12) = m1 + m7 + m1 2 = A BC  D + ABCD + ABC  D AB CD 00 01 11 10 00011110 解：由表达式中的 知该函数为四变量函数所以需要四变量卡诺图观 察得知表达式已是最小项表达式只需将每一个最小项填入卡诺图即可 在ABCD对应0001的方格里填1即表示最小项即 m12 m1 =ABCD 同样在0111和1100的方格中填1即得下图（其余填0，通常可省略） 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0

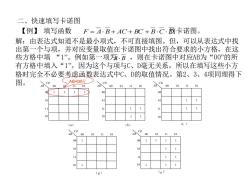
二、快速填写卡诺图 【例】填写函数F=A.B+AC+BC+B.C.的卡诺图。 解：由表达式知道不是最小项式，不可直接填图。但，可以从表达式中找 出第一个与项，并对应变量取值在卡诺图中找出符合要求的小方格，在这 些方格中填“1”。例如第一项.B,则在卡诺图中对应AB为“00的所 有方格中填入“1”，因为这个与项与C、D毫无关系，所以在填写这些小方 格时完全不必要考虑函数表达式中C、D的取值情况。第2、3、4项同理得下 图。 AB=00行 CD 110 00 01 11 10 00 01 11 10 1 00 00 10 10 (a) (b) (c) CD 00 01 11 10 00 01 11 10 00 00 01 01 10 10 (d) (e)

二、快速填写卡诺图 【例】 填写函数 F = A B + AC + BC + BC D 的卡诺图。 解：由表达式知道不是最小项式，不可直接填图。但，可以从表达式中找 出第一个与项，并对应变量取值在卡诺图中找出符合要求的小方格，在这 些方格中填 “1”。例如第一项为 ，则在卡诺图中对应AB为“00”的所 有方格中填入“1”，因为这个与项与C、D毫无关系，所以在填写这些小方 格时完全不必要考虑函数表达式中C、D的取值情况。第2、3、4项同理得下 图。 A B 00 01 11 10 00 01 10 11 AB CD （a） 1 1 1 1 00 01 11 10 00 01 10 11 AB CD （b） 1 1 1 1 00 01 11 10 00 01 10 11 AB CD （c ） 1 1 1 1 00 01 11 10 00 01 10 11 AB CD （d ） 1 1 00 01 11 10 00 01 10 11 AB CD 1 1 1 1 1 1 1 1 1 1 1 （e ） AB=00行

用卡诺图化简逻辑函数步骤 1.画卡诺图 根据给定的逻辑函数确定变量的个数，然后画出相应的卡诺图，利用快 速填卡诺图法填图。 2.画卡诺圈 对卡诺图中有“1”的方格画相邻区域圈。遵循的原则是：以2、4、8、 16格(2)为单位；圈越大越好；圈数越少越好（避免多余项的出现）。 3.读卡诺圈，写结果 将每个圈中的公有变量因子找出来，得到对应的“与”项，并把各个圈 得到的与项相加（或）起来，便得到化简后的最简与或表达式

用卡诺图化简逻辑函数步骤 1. 画卡诺图 根据给定的逻辑函数确定变量的个数，然后画出相应的卡诺图，利用快 速填卡诺图法填图。 2. 画卡诺圈 对卡诺图中 有“1” 的方格画相邻区域圈。遵循的原则是：以2、4、8、 16格（2 n）为单位；圈越大越好；圈数越少越好（避免多余项的出现）。 3. 读卡诺圈，写结果 将每个圈中的公有变量因子找出来，得到对应的“与”项，并把各个圈 得到的与项相加（或）起来，便得到化简后的最简与或表达式