《物理化学》课程教学课件（PPT讲稿）第二章 热力学第二定律 The Second Law of Thermodynamics

《热力学第一定律》基本教学要求 1.基本概念：状态函数和过程量，等温过程， 等压过程，绝热过程，可逆过程 2.基本内容：W、Q、△U和△H的计算，理想 气体各种过程的计算 3.基本方法：解题“三步曲” 求△U和△H经常使用设计途径的方法 (求W和Q不可使用设计途径的方法) 科学表述

1 《热力学第一定律》基本教学要求 1. 基本概念：状态函数和过程量，等温过程， 等压过程，绝热过程，可逆过程 2. 基本内容：W、Q、U和H的计算，理想 气体各种过程的计算 3. 基本方法：解题“三步曲” 求U和H经常使用设计途径的方法 (求W和Q不可使用设计途径的方法) 科学表述

第二章 热力学第二定律 Chapter 2 The Second Law of Thermodynamics >不违背第一定律的事情是否一定能成功呢？ 例1.H2(g)+1/202(g→】 H200① △Hm(298K)=-286kJmo1 加热，不能使之反向进行。 例2.25C及9下，Ht+O→H,0①极易进行， 但最终H][OH=1014mol2.dm-6,即 反应不进行到底。 >第二定律的任务：方向，限度 2

2 第二章 热力学第二定律 Chapter 2 The Second Law of Thermodynamics ➢ 不违背第一定律的事情是否一定能成功呢？ 例1. H2 (g) + 1/2O2 (g) H2O(l) rH m(298K) = -286 kJ.mol-1 加热，不能使之反向进行。 例2. 25 C及p 下，H+ + OH- H2O(l)极易进行， 但最终[H+ ][OH- ] = 10-14 mol2 .dm-6，即 反应不进行到底。 ➢ 第二定律的任务：方向，限度

§2.1自发过程的共同特征 一、自发过程的方向和限度 人类经验说明：自然界中一切变化都是有方向和限度的，且是自动 发生的，称为“自发过程”Spontaneous process。 >自发过程(spontaneous process))：在一定环境条件下，（环境） 不作非体积功，系统中自动发生的过程。反之，只有（环境）作 非体积功方能发生的过程为非自发过程。通常所说的“过程 方向”即是指自发过程的方向。 限度 ①气流：高压→ 低压 压力相同 ②传热：高温一 低温 温度相同 ③扩散： 高浓度 低浓度 浓度相同 ④反应：HCI+NaOH→NaCI+H,O 化学平衡 3

3 §2.1 自发过程的共同特征 一、自发过程的方向和限度 ➢ 自发过程(spontaneous process)：在一定环境条件下，(环境) 不作非体积功，系统中自动发生的过程。反之，只有(环境)作 非体积功方能发生的过程为非自发过程。通常所说的“过程 方向”即是指自发过程的方向。 ① 气流：高压 低压 压力相同 ② 传热：高温 低温 温度相同 ③ 扩散：高浓度 低浓度 浓度相同 ④ 反应：HCl + NaOH NaCl + H2O 化学平衡 人类经验说明：自然界中一切变化都是有方向和限度的,且是自动 发生的,称为“自发过程” Spontaneous process 。 限度

>具有普遍意义的过程：热功转换的不等价性 功无代价，全部 热 不可能无代价，全部 ①W二Q不等价，是长期实践的结果。 ②不是Q1 W不可能，而是热全部变功必 须付出代价（系统和环境），若不付代价只能 部分变功。 “功可以自发地全部变为热，但热不可能全部变为功，而不 留任何其它变化”。 一切自发过程都是不可逆过程，而且他们的不可逆性均可 归结为热功转换过程的不可逆性，因此，他们的方向性都可用热 功转化过程的方向性来表达

4 “功可以自发地全部变为热，但热不可能全部变为功，而不 留任何其它变化”。 一切自发过程都是不可逆过程, 而且他们的不可逆性均可 归结为热功转换过程的不可逆性, 因此,他们的方向性都可用热 功转化过程的方向性来表达。 ➢ 具有普遍意义的过程：热功转换的不等价性 功 无代价，全部 热 不可能无代价，全部 ① W Q 不等价，是长期实践的结果。 ② 不是 Q W 不可能，而是热全部变功必 须付出代价(系统和环境)，若不付代价只能 部分变功

二、自发过程的共同特征 (General character of spontaneous process) (①)自发过程单向地朝着平衡。 (2)自发过程都有作功本领。 (3)自发过程都是不可逆的。 5

5 二、自发过程的共同特征 (General character of spontaneous process) (1) 自发过程单向地朝着平衡。 (2) 自发过程都有作功本领。 (3) 自发过程都是不可逆的

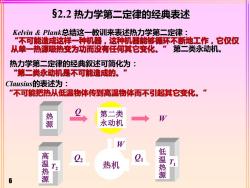
§2.2热力学第二定律的经典表述 Kelvin&Plank总结这一教训来表述热力学第二定律： “不可能造成这样一种机器，这种机器能够循环不断地工作，它仅仅 从单一热源吸热变为功而没有任何其它变化。”第二类永动机。 热力学第二定律的经典叙述可简化为： ”第二类永动机是不可能造成的。” Clausius的表述为： “不可能把热从低温物体传到高温物体而不引起其它变化。” 第二类 永动机 W 源 W 高温热 22 热机 低温热源 T 6

6 Kelvin & Plank总结这一教训来表述热力学第二定律： “不可能造成这样一种机器，这种机器能够循环不断地工作，它仅仅 从单一热源吸热变为功而没有任何其它变化。” 第二类永动机。 热力学第二定律的经典叙述可简化为： “第二类永动机是不可能造成的。” Clausius的表述为： “不可能把热从低温物体传到高温物体而不引起其它变化。” §2.2 热力学第二定律的经典表述 热 源 第二类 永动机 Q W 高 温 热 源 热机 Q2 T2 W 低 温 热 源 T1 Q1

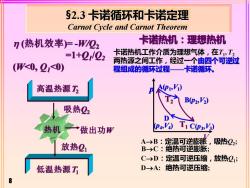
§2.3卡诺循环和卡诺定理 Carnot Cycle and Carnot Theorem n(热机效率)=-W/02 卡诺热机：理想热机 =1+0/02 卡诺热机工作介质为理想气体，在T,T2 两热源之间工作，经过一个由四个可逆过 (W<0,2<0) 程组成的循环过程—卡诺循环。 高温热源2 12 B(P2,V2) 吸热22 D下 热机一→做出功W PAVA TiCO0,囹 放热21 A→B:定温可逆膨涨， 吸热Q2; B-→C:绝热可逆膨胀； C→D:定温可逆压缩，放热21； 低温热源 D→A:绝热可逆压缩；

8 §2.3 卡诺循环和卡诺定理 Carnot Cycle and Carnot Theorem  (热机效率)= -W/Q2 =1+Q1 /Q2 (W<0, Q1<0) 低温热源T1 高温热源T2 吸热Q2 放热Q1 做出功W 卡诺热机：理想热机 卡诺热机工作介质为理想气体，在T1 , T2 两热源之间工作，经过一个由四个可逆过 程组成的循环过程——卡诺循环。 p V A(p1 ,V1 ) B(p2 ,V2 ) T1 C(p3 ,V3 ) D (p4 ,V4 ) T2 B→C：绝热可逆膨胀; D→A: 绝热可逆压缩; A→B：定温可逆膨胀，吸热Q2 ; C→D：定温可逆压缩，放热Q1 ;

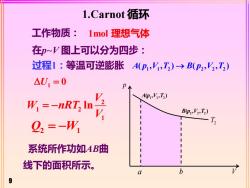
1.Carnot循环 工作物质：1mol理想气体 在印~V图上可以分为四步： 过程1：等温可逆膨胀A(P,Y,I)→B(P2,2,T) △U1=0 W.=-nRT, A,T2) B(p,V,T) Q2=-W T 系统所作功如AB曲 线下的面积所示。 a b 9

9 工作物质： 过程1：等温可逆膨胀 1 1 2 2 2 2 A p V T B p V T ( , , ) ( , , ) → 1  = U 0 2 1 2 1 lnV W nRT V = − 系统所作功如AB曲 线下的面积所示。 Q W 2 1 = − 1.Carnot 循环 在p~V 图上可以分为四步： 1mol 理想气体 p 1 1 2 A p V T ( , , ) 2 2 2 B p V T ( , , ) V T2 a b

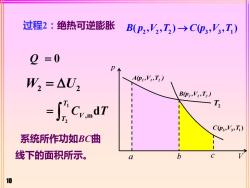
过程2：绝热可逆膨胀 B(p2,V,T2)→Cp3,V,T) 2 =0 W,=△U, Ap1,',T2) Bp2,V2,T2) T C3,T) 系统所作功如BC曲 线下的面积所示。 a b 10

10 过程2：绝热可逆膨胀 2 2 2 3 3 1 B p V T C p V T ( , , ) ( , , ) → Q = 0 W U 2 2 =  系统所作功如BC曲 线下的面积所示。 1 2 ,md T V T = C T  p A(p ,V ,T ) 1 1 2 B(p ,V ,T ) 2 2 2 3 3 1 C p V T ( , , )V T2 a b c

过程3：等温可逆压缩 C(P3,V,T)→Dp4,V4,T) △U3=0 A(PV,T) W3=-nRT In Bp2,'3,T2) T 2=-W3 D(PVT) C0,',T) 环境对系统所作功如 DC曲线下的面积所示 a d b C 11

11 3  = U 0 环境对系统所作功如 DC曲线下的面积所示 Q W 1 3 = − 4 3 1 3 lnV W nRT V = − 过程3：等温可逆压缩 3 3 1 4 4 1 C p V T D p V T ( , , ) ( , , ) → p 1 1 2 A p V T ( , , ) 2 2 2 B p V T ( , , ) 3 3 1 C p V T ( , , ) 4 4 1 D p V T ( , , ) V T2 T1 a d b c