《材料研究方法》课程教学课件（讲稿）第六章-高分辨电子显微技术（电子显微图像的分辨极限）

一、 电子显微图像的分辨极限 1、高分辨像的形成 第六章高分辨电子显微技术 一、电子显微图像的分辨极限 二、高分辨图像解释 三、高分辨技术的应用 ()明场方法；(b)晴场方法：()高分娜电子显微方法 对于薄试样： 置 Ψ(x,y)-exp(iop(x,y)△z) xy亦：透射函数(transmission function): a:相互作用常数(interaction constant),与电镜的加速电乐成反比： 9xyW:沿厚度方向(2方向)的物质投影势 受影赶先金 当试样厚度在2、3nm以下时. x,y1+ioo(Ky)△z Abbs theory of imape frmation 由此可见，电压越低，物质的内势就越大， 入射电子的位相的变化航越大。 2、高分辨像的分辨极限 如果不考虑： (1)像的放大作用： (2)物锁光阑的作用. (I)射分辨极限(Diffraction limit) 则，像强度为： (2)球差(Spherical aberration) I(Xy)≈1±2o0(X,y)△z (3)色差(Chromatic aberration) (4)象散(Astigmatism) 由此可见：像的强度是试样的物质势和厚度的线性函激。 (S)欠焦量(Decs)

第六章 高分辨电子显微技术 一、电子显微图像的分辨极限 二、高分辨图像解释 三、高分辨技术的应用 一、电子显微图像的分辨极限 1、高分辨像的形成 对于薄试样： Ψ(x,y)=exp(iσϕ(x,y)∆z) Ψ(x,y)：透射函数（transmission function）； σ：相互作用常数(interaction constant) ，与电镜的加速电压成反比； ϕ(x,y)：沿厚度方向（z方向）的物质投影势 因此：由于试样的存在，入射电子波较之真空传播的情 况，只发生了位相变化，这个位相变化量为σϕ(x,y)∆z。 当试样厚度在2、3nm以下时, Ψ(x,y)≈1+iσϕ(x,y)∆z 由此可见，电压越低，物质的内势就越大， 入射电子的位相的变化就越大。 如果不考虑： （1）像的放大作用； （2）物镜光阑的作用。 则，像强度为： I(x,y)≈1±2 σϕ(x,y)∆z 由此可见：像的强度是试样的物质势和厚度的线性函数。 2、高分辨像的分辨极限 （1） 衍射分辨极限（Diffraction limit Diffraction limit Diffraction limit Diffraction limit） （2） 球差（Spherical aberration Spherical aberration Spherical aberration Spherical aberration） （3） 色差（Chromatic aberration Chromatic aberration Chromatic aberration Chromatic aberration） （4） 象散（Astigmatism Astigmatism Astigmatism Astigmatism） （5）欠焦量 （Defocus Defocus Defocus Defocus）

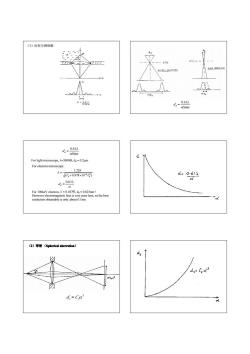
(1)衍射分辨极限 JUST RESOLVED FASILY起SOLVE Md H 0.612 d,= nSina 4=06u nSina d For light microscope,5000,da0.2um. For electron microscope: 1.226 V6+0.978×10-8 d:0611 d= 0.61入 a For100 keV electron.,入z0.037e,d≈0.023nm1 However electromagnetic lens is very poor lens,so the best resolution obtainable is only about 0.1nm. (2)球差(Spherieal aberration) d Hcd d,=Ca

（1）衍射分辨极限 α λ nSin d d 0.61 = α λ nSin d d 0.61 = For light microscope, λ≈5000⊕, dd ≈ 0.2µm. For electron microscope: ( 0.978 10 ) 1.226 2 0 6 V0 V− + × λ = α 0.61λ dd = For 100keV electron, λ ≈ 0.037⊕, dd ≈ 0.023nm ! However electromagnetic lens is very poor lens, so the best resolution obtainable is only about 0.1nm. （2）球差 （Spherical aberration Spherical aberration Spherical aberration Spherical aberration） 3 d s = Csα

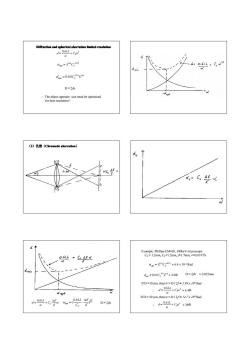
Diffraction and spherical aberration limited resolution d=062+Ca a a="4C4 d:61+C,3 d min dm=0.65C,44 D=2/ .The object aperture size must be optimized dopt for best resolution！ (3)色差(Chromatic aberration) de 个 a d↑ Example:Phillips EM430,300keV microscope o61以+G&△EX Cs=1.2mm,Cc-1.2mm,戶1.7mm入=0.0197A E =4C46.4x 103 Rad d min 一一 d=0.65C,"“≈2.0e D=2a*0.022mm If D=10 um,then a =D/2f-2.94x /0Rad. d-0.61Z+Ca4 以et d-061a 管0&=645 If D=50 um,then a=D/2f=/4.7x /0Rad. Ce E D=2 4-062+Cs39m a

1/ 4 −1/ 4 αopt = λ CS 1/ 4 3/ 4 d min = 0.65CS λ Diffraction and spherical aberration limited resolution Diffraction and spherical aberration limited resolution Diffraction and spherical aberration limited resolution Diffraction and spherical aberration limited resolution 61 3 0. α α λ CS d = + D = 2fα ∴ The object aperture size must be optimized for best resolution ! （3）色差（Chromatic aberration Chromatic aberration Chromatic aberration Chromatic aberration） α α λ E E d CC ∆ = + 0.61 2 1 ) 0.61 ( E E CC opt ∆ = ⋅ λ α D = 2fα Example: Phillips EM430, 300keV microscope CS = 1.2mm, CC=1.2mm, f=1.7mm, λ=0.0197Å 1/ 4 −1/ 4 αopt = λ CS ≈ 6.4 x 10-3 Rad 1/ 4 3/ 4 d min = 0.65CS λ ≈ 2.0⊕ D = 2fα ≈ 0.022mm If D =10 µm, then α = D / 2f = 2.94 x 10-3Rad, ∴ 61 3 0. α α λ CS d = + ≈ 4.4⊕ If D = 50 µm, then α = D / 2f = 14.7 x 10-3Rad, ∴ 61 3 0. α α λ CS d = + ≈ 39⊕

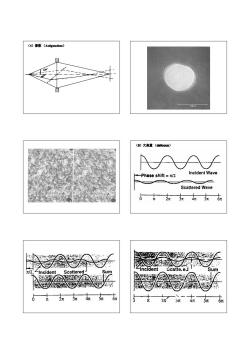
(4)像散（(Astigmatism) (5)欠焦量(defocus) 。-Phase shift=元2 Incident Wave Scattered Wave incldent Scatte.ed Sum 2 Incldent Scattered- Sum 6玩玩东标 个 2π3π4 5π 6元

（4）像散 （Astigmatism Astigmatism Astigmatism Astigmatism） （5）欠焦量 （defocus defocus defocus defocus）

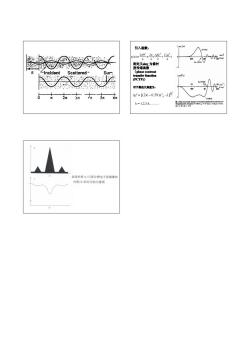
引入函数 玉产二 《22Ψ”2年合之+ 2 则定义s为像村 度传递函激 公 -Incident Scattered- Sum (phase contrast transfer function (PCTF)) 对于最佳软焦量为： 4/=(2k-0.59)C,·1J k=1,23,4 等威 晶体的势(a)与高分辨电子显微像的 材度(b)间对应的示意图

引入函数： ) 2 4 ( 2 2 ( ) 2 4 α α λ π λ π χ CS f u + ∆ = Ψ′ = 则定义sinχ 为像衬 度传递函数 （phase contrast phase contrast phase contrast phase contrast transfer function transfer function transfer function transfer function (PCTF)） 2 1 ∆ = [(2 − 0.59) ⋅ λ] CS f k k = 1,2,3,4,. 对于最佳欠焦量为：