《工程塑性理论》课程试卷习题（A卷答案）

内蒙古科技大学考试标准答案及评分标准 课程名称：《工程塑性理论》A卷 考试班级：成型2005-1、2、3班 考试时间：年月日时分至时分标准制订人：曹建刚 一、名词解释(30分每题3分) 1、直线滑移线场：由两族正交直线构成的滑移线场，它所对应的应力场为均匀直线场。 2、位移：变形体内任意一点变形前后的直线距离。 3、等效应力：将复杂应力状态等效为单向拉伸屈服应力0。 a.=5a,-o,广+a,-a广+(a:-a,)广+6（民++r川 4、主平面：剪应力为零的平面。 5、静水压力：三个方向正应力为压应力，并等于三个正应力的平均值，即p==1/3(+,+0,. 6、位移增量：变形体中一质点在某一解间，经过无限小时间dt所产生的位移量为位移增量Ui。 7、应变增量：变形体中一质点在某一瞬间，经过无限小时间dt所产生的应变量为应变增量de4: 8、屈服表面：在应力空间中屈服函数为一曲面，此曲面为屈服表面， 9、滑移线的转角：α族滑移线与x轴正向的夹角。 10、上界定理：运动学许可的速度场所确定的功率总是大于等于真实功率。 得分点：每小思3分，只要意思答对均得分。 二、回答下列问题(32分每题8分) 1、如何完整地表示受力物体内一点的应力状态？ 物体内一点的应力状态可以用一个二阶张量。：九个应力分量来表示。 Os Og Ge 0g= ·0J 得分点：只写出二阶张量0得4分：九个分量全部写出得8分。 2、写出平面变形条件下的力平衡微分方程。 .=0 dydy

内蒙古科技大学考试标准答案及评分标准 课程名称：《工程塑性理论》A 卷 考试班级：成型 2005－1、2、3 班 考试时间： 年 月 日 时 分至 时 分 标准制订人：曹建刚 一、名词解释（30 分每题 3 分） 1、直线滑移线场：由两族正交直线构成的滑移线场，它所对应的应力场为均匀直线场。 2、位移：变形体内任意一点变形前后的直线距离。 3、等效应力：将复杂应力状态等效为单向拉伸屈服应力σs。 4、主平面：剪应力为零的平面。 5、静水压力：三个方向正应力为压应力，并等于三个正应力的平均值，即 p=σm=1/3(σx+σy+σz). 6、位移增量：变形体中一质点在某一瞬间，经过无限小时间 dt 所产生的位移量为位移增量 dUi。 7、应变增量：变形体中一质点在某一瞬间，经过无限小时间 dt 所产生的应变量为应变增量 dεij。 8、屈服表面：在应力空间中屈服函数为一曲面，此曲面为屈服表面。 9、滑移线的转角：α族滑移线与 x 轴正向的夹角。 10、上界定理：运动学许可的速度场所确定的功率总是大于等于真实功率。 得分点：每小题 3 分，只要意思答对均得分。 二、回答下列问题（32 分每题 8 分） 1、如何完整地表示受力物体内一点的应力状态？ 物体内一点的应力状态可以用一个二阶张量σij 九个应力分量来表示。 得分点：只写出二阶张量σij 得 4 分；九个分量全部写出得 8 分。 2、写出平面变形条件下的力平衡微分方程。 1 2 2 2 2 2 2 [( ) ( ) ( ) 6( )] 2           e x y y z z x xy yz zx = − + − + − + + + . . . x xy xz ij y yz z            =       0 0 x xy yx y x y y y       + =     + =  

得分点：写出三维力平衡微分方程方程只得4分；正确写出平面变形条件下的力平衡微分方程得8 3、变形体Z方向的正应变为0，试证明该方向的正应力为0，=1/2(0，+0，)。 证明：Z方向无变形e.0,因此0.'=0 (1) 0.’=0.-0。,0,-0.=0 (2) 0.=0t0,+0, 宽度方向的应力为：0，=1/2(+o,)。 (3) 得分点：第(1)步得3分：第(2)步得3分：第(3)步得2分： 4、写出Mises屈服条件与Tresca屈服条件。 Tresca屈服条件 (01-03)=g Mises屈服条件：(a,-o,)+(0o)+（o,o)=2o2或 a=互a-,+(,-+(a-广+6(++) 得分点：写出Tre3ca屈服条件得4分：写出Mises屈服条件得4分.。 三、如图所示平砧压缩矩形件(L/h>1)时， L 1、讨论接触表面摩擦规律及摩擦规律与正压力之间的关系(8分) 平砧压缩矩形件当L/h较大时，工具与工件接触表面摩擦存在三个区域，即滑动区、粘着区、 摩擦应力递减区 滑动区对应的正应力为指数分布、粘着区对应的正应力为直线分布、摩擦应力递减区对应的正应 力为抛物线分布。(4分) 得分点：正确答出工具与工件接触表面摩擦存在三个区域得4分；正确答出不同摩擦所对应的正应力 分布得4分。 2、接触表面为全粘着，试推导接触表面的单位压力分布方程。(10分) 解：从变形区内截取单元体作受力分析如图。列出单元体的微分平衡方程 (o,+do,)h-ho,+2 tdx=0 hd o,+2t dx=0 Tresca屈服条件a1o,=0,0=-0,0=-o,s,0,=0

得分点：写出三维力平衡微分方程方程只得 4 分；正确写出平面变形条件下的力平衡微分方程得 8 分。 3、变形体 Z 方向的正应变为 0，试证明该方向的正应力为σz=1/2(σx+σy)。 证明：Z 方向无变形εz=0，因此σz’=0 （1） σz’=σz-σm ，σz-σm =0 （2） σm =σx+σy+σz 宽度方向的应力为： σz=1/2（σx+σy）。 （3） 得分点：第（1）步得 3 分；第（2）步得 3 分；第（3）步得 2 分； 4、写出 Mises 屈服条件与 Tresca 屈服条件。 Tresca 屈服条件: Mises 屈服条件:（σ1-σ2）2 +（σ2-σ3）2 +（σ3-σ1）2 =2σs 2 或 得分点：写出 Tresca 屈服条件得 4 分；写出 Mises 屈服条件得 4 分。 三、如图所示平砧压缩矩形件（L / h ＞ 1）时， 1、讨论接触表面摩擦规律及摩擦规律与正压力之间的关系（8 分） 平砧压缩矩形件当 L / h 较大时，工具与工件接触表面摩擦存在三个区域，即滑动区、粘着区、 摩擦应力递减区。 滑动区对应的正应力为指数分布、粘着区对应的正应力为直线分布、摩擦应力递减区对应的正应 力为抛物线分布。（4 分） 得分点：正确答出工具与工件接触表面摩擦存在三个区域得 4 分；正确答出不同摩擦所对应的正应力 分布得 4 分。 2、接触表面为全粘着，试推导接触表面的单位压力分布方程。（10 分） 解：从变形区内截取单元体作受力分析如图。列出单元体的微分平衡方程 (σx+dσx)h-hσx+2τfdx=0 hdσx+2τfdx=0 Tresca 屈服条件 σ1-σ3=σs σ1=-σx σ3=-σy σy-σx=σs h L

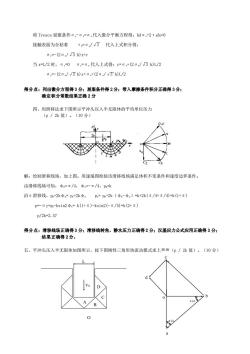
将Tresca屈服条件o,o,=o,代入微分平衡方程得：hdo,+2tdx=0 接触表面为全粘者 /3代入上式积分得： o,=-(2o,/、3h)x+c 当x/2时，o,=0,.代入上式得：c=o+(2/3hL/2 o,=-(2o,/√3h)x+o,+(2o,/3h)L/2 得分点：列出徽分方程得3分屈服条件得2分，带入摩擦条件积分正确得3分 确定积分常数结果正确2分 四、用滑移法求下图所示平冲头压入半无限体的平均单位压力 (p/2张值)。(10分) 解：绘制滑移线场，如上图。用速端图检验该滑移线场满足体积不变条件和速度边界条件。 由滑移线场可知，中=n/4,中r/4,水 沿a滑移线，p+2k中=Px+2k中cP=p+2k(中-中c)=k+2k(π/4+I/4)=k(1+I） p-oy=-ksin2中=k(1+n)-ksin2(←/4④=k(2+x) p/2k=2.57 得分点：滑移线场正确得3分滑移线转角、静水压力正确得2分汉基应力公式应用正确得3分： 结果正确得2分。 五、平冲头压入半无限体如图所示，按下图刚性三角形块流动模式求上跟信(p/2k值)。(10分)

将 Tresca 屈服条件σy-σx=σs 代入微分平衡方程得：hdσy+2τfdx=0 接触表面为全粘着 τf=σs/√3 代入上式积分得： σy=-(2σs/√3 h)x+c 当 x=L/2 时，σx=0 σy=σs 代入上式得：c=σs+(2σs/√3 h)L/2 σy=-(2σs/√3 h)x+σs+(2σs/√3 h)L/2 得分点：列出微分方程得 3 分；屈服条件得 2 分；带入摩擦条件积分正确得 3 分； 确定积分常数结果正确 2 分 四、用滑移法求下图所示平冲头压入半无限体的平均单位压力 （p / 2k 值）。（10 分） 解：绘制滑移线场，如上图。用速端图检验该滑移线场满足体积不变条件和速度边界条件。 由滑移线场可知，φE=π/4，φC=-π/4，pE=k 沿α滑移线，pE+2kφE= pC+2kφC pC= pE+2k（φE-φC）=k+2k(π/4+π/4)=k(1+π) p=-σy=pC-ksin2φC= k(1+π)-ksin2(-π/4)=k(2+π) p/2k=2.57 得分点：滑移线场正确得 3 分；滑移线转角、静水压力正确得 2 分；汉基应力公式应用正确得 3 分； 结果正确得 2 分。 五、平冲头压入半无限体如图所示，按下图刚性三角形块流动模式求上界值（p / 2k 值）。（10 分） d c a π/4 π/4 o b D C B A V0 O L

解：根据流动模式绘制出速端图 由流动模式可知AB=BC-CD=OD2L/2 OB=OC=L 由速端图得 ab=bc=2 Vo oa=ob=oc=Vo cd=od=2 Vo/2 上界功率=2k(B×ab+0B×ob+-BCXbe+0CXoc+CDXcd+-0DXod) W=2k(2L/2x2Vo+L×Vo+2L/2×√2Vo+L×Vo+J2L/2×2V%/2+ 2L/2×2V/2) W=10kL Vo pX Vo=W p=10kLVo/Vo=10k p/2k=5 得分点：速端图正确得3分：流动慎块边长、速度计算正确得2分；上界功率公式正确得3分： 结果计算正确得2分

解： 根据流动模式绘制出速端图。 由流动模式可知 AB=BC=CD=OD=√2 L/2 OB=OC=L 由速端图得 ab=bc=√2 V0 oa=ob=oc= V0 cd=od=√2 V0/2 上界功率 W=2k(AB×ab+OB×ob+BC×bc+OC×oc+CD×cd+OD×od) W=2k(√2 L/2×√2 V0+ L×V0+√2 L/2×√2 V0+ L×V0+ √2 L/2×√2 V0/2+ √2 L/2×√2 V0/2) W=10kL V0 p×V0=W p=10kLV0/V0=10k p/2k=5 得分点：速端图正确得 3 分；流动模块边长、速度计算正确得 2 分；上界功率公式正确得 3 分； 结果计算正确得 2 分