阜阳师范大学（阜阳师范学院）：《数学教学测试与评价》课程教学资源（PPT课件）第三讲 数学测验的设计和统计指标（3.3-3.4）、第四讲 中学生数学学业评价

§3.3数学题的拟造 试题 改编陈题 ·变更结论，变更条件，同时变更条件和结论 ·编制新题 ·利用实际问题，利用数学自身问题 。数学开放题 ■试卷：结构、设计、编制、审核、难度预测

§ 3.3 数学题的拟造 ◼ 试题 ◼ 改编陈题 ◼ 变更结论，变更条件，同时变更条件和结论 ◼ 编制新题 ◼ 利用实际问题，利用数学自身问题 ◼ 数学开放题 ◼ 试卷：结构、设计、编制、审核、难度预测

G.Polya:"怎样解题“表 解题过程：①弄清解题②拟定计划③实现计划 ④回顾一四个阶段 解题表的精华是第二部分一变更题目：以熟悉 对付陌生（思维的一般规律） ■变更题日的方法（见下一片，天-P117) 例子：任何△ABC中有内切圆O,圆O1、O2、 O,分别与三角形两边及圆O相切，对应的半径 分别为R、R1、R2R3求证：R≤R+R2+R3

G. Polya： ”怎样解题“表 ◼ 解题过程：①弄清解题②拟定计划③实现计划 ④回顾—四个阶段 ◼ 解题表的精华是第二部分—变更题目：以熟悉 对付陌生（思维的一般规律） ◼ 变更题目的方法（见下一片，天-P117） ◼ 例子：任何△ABC中有内切圆O，圆O1、O2、 O3分别与三角形两边及圆O相切，对应的半径 分别为R、R1、R2、R3求证：R≤R1+R2+R3

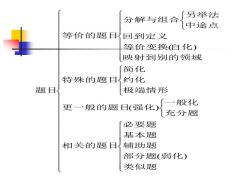
分解与组合 「另举法 中途点 等价的题目回到定义 等价变换（自化） 映射到别的领或 简化 特殊的题目约化 题目 极惴情形 般化 更一般的题目（强化） 充分题 必要题 基本题 相关的题目辅助题 部分题（弱化） 类以题

                                                      类似题 部分题 弱化 辅助题 基本题 必要题 相关的题目 充分题 一般化 更一般的题目 强化 极端情形 约化 简化 特殊的题目 映射到别的领域 等价变换自化 回到定义 中途点 另举法 分解与组合 等价的题目 题目 ( ) ( ) ( )

变更的题目（天本-p117-121) 题目1（基本题） ■题目2（等价题） ■题目3（充分题） ■题目4（等价题） ■题目5、6（充分题） ■题目7、8、9（引申题）

变更的题目（天本-P117-121） ◼ 题目1（基本题） ◼ 题目2（等价题） ◼ 题目3（充分题） ◼ 题目4（等价题） ◼ 题目5、6（充分题） ◼ 题目7、8、9（引申题）

试题的功能：考查内容 例1在直角梯形ABCD中，中位线MN=2AD=4, 斜腰AB-AD+BC,求CD长和∠ABC的度数。 (任-P101) ■例1-1（变更一）：在直角梯形ABCD中，斜腰 AB=8,BC-AD=4,求CD的长。 ■例1-2（变更二）：以AB为直径的圆N与DC相切于 M,AD、BC都是DC的垂线，且AD、BC的长度 是方程x2-8x+12=0的两根，问：①CD的长②如 果BC与圆N还有不同于B的交点E,求证：△NBE 是等边△

试题的功能：考查内容 ◼ 例1 在直角梯形ABCD中，中位线MN=2AD=4， 斜腰AB-AD+BC，求CD长和ABC的度数。 （任-P101） ◼ 例1-1(变更一):在直角梯形ABCD中，斜腰 AB=8，BC-AD=4，求CD的长。 ◼ 例1-2(变更二):以AB为直径的圆N与DC相切于 M，AD、BC都是DC的垂线，且AD、BC的长度 是方程x 2 -8x+12=0的两根，问:①CD的长②如 果BC与圆N还有不同于B的交点E,求证: △ NBE 是等边△

试题的功能：考查目标 例2已知函数y=(x-1)/(2x1)(x≠1/2)，证 明：①经过这个函数图象上任意两个不 同的点的直线不平行于x轴；②这个函数 图象关于直线y=x成轴对称图形。 ■本题考查函数图象的性质、平行直线和 对称图形以及逻辑推理能力。 ■从知识看属于理解，从方法上可靠向掌 握。从整体上看，介于理解与掌握之间

试题的功能：考查目标 ◼ 例2 已知函数 y=(x-1)/(2x-1) (x1/2),证 明： ①经过这个函数图象上任意两个不 同的点的直线不平行于x轴;②这个函数 图象关于直线y=x成轴对称图形。 ◼ 本题考查函数图象的性质、平行直线和 对称图形以及逻辑推理能力。 ◼ 从知识看属于理解，从方法上可靠向掌 握。从整体上看，介于理解与掌握之间

试题结构：题设和提问 一、题设的特点 明确性、准确性、简洁性、独立性（恰当、 条理) ■二、提问的特点 ·指令明确、要求恰当、问题可解 ·三、试题的质量 ·科学性、适纲性、有效性、针对性、严谨性 背景公平、形式新颖、优美自然（数学美）

试题结构：题设和提问 ◼ 一、题设的特点 ◼ 明确性、准确性、简洁性、独立性（恰当、 条理） ◼ 二、提问的特点 ◼ 指令明确、要求恰当、问题可解 ◼ 三、试题的质量 ◼ 科学性、适纲性、有效性、针对性、严谨性 ◼ 背景公平、形式新颖、优美自然（数学美）

开放题一数学教学的新模式 开放的背景 全国九五规划重点课题 课改、大纲、课标一将开放题纳入其中 ■ 数学开放题(open-ended problem)的特 点（戴-P33) 数学开放式教学模式(open-approach method)：钟面数字问题（戴-P55) ■用开放性问题进行数学教学评价

开放题—数学教学的新模式 ◼ 开放的背景 ◼ 全国九五规划重点课题 ◼ 课改、大纲、课标—将开放题纳入其中 ◼ 数学开放题(open-ended problem)的特 点（戴-P33） ◼ 数学开放式教学模式 （open-approach method）：钟面数字问题（戴-P55） ◼ 用开放性问题进行数学教学评价

试卷 (任-P142) 试卷的结构：框架，题型，知识，能力， 难度 ■试卷的设计：设计原理，设计技术一细 目表 试卷的编制：组题拼卷，试题调整，赋 分与评分标准 ■ 试卷的难度预测：试题难度，试卷长度， 考生程度，判卷尺度

试卷（任-P142） ◼ 试卷的结构：框架，题型，知识，能力， 难度 ◼ 试卷的设计：设计原理，设计技术—细 目表 ◼ 试卷的编制：组题拼卷，试题调整，赋 分与评分标准 ◼ 试卷的难度预测：试题难度，试卷长度， 考生程度，判卷尺度

试卷的难度预测 是将试卷中各道试题的预测难度加权平 均，所得平均值便可作为试卷难度的预 测值。即： 若试卷由n道试题组成，各题的满分值依 次为X1,X2.X,而各题的难度预测值依次 为pP2Pnv.则试卷难度预测值可取用 试题预测难度均值p=∑uPv 其中u=X/∑x,I=1,2.n

试卷的难度预测 ◼ 是将试卷中各道试题的预测难度加权平 均，所得平均值便可作为试卷难度的预 测值。即： ◼ 若试卷由n道试题组成，各题的满分值依 次为x1 , x2.xn , 而各题的难度预测值依次 为p1 ,p2.pn ,则试卷难度预测值可取用 试题预测难度均值p=ipi , 其中i= xi / xi ,I=1,2.n