南京大学：《高级算法 Advanced Algorithms》课程教学资源（课件讲稿）03 Balls-into-Bins Model and Chernoff Bounds

Balls-into-Bins Model and Chernof肝Bounds Advanced Algorithms Nanjing University,Fall 2022

Balls-into-Bins Model and Chernoff Bounds Advanced Algorithms Nanjing University, Fall 2022

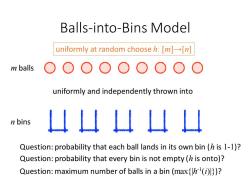
Balls-into-Bins Model uniformly at random choose h:[m][n] m balls uniformly and independently thrown into n bins Question:probability that each ball lands in its own bin (h is 1-1)? Question:probability that every bin is not empty (h is onto)? Question:maximum number of balls in a bin(maxh()?

Balls-into-Bins Model m balls n bins uniformly and independently thrown into uniformly at random choose h: [m]→[n] Question: probability that each ball lands in its own bin (h is 1-1)? Question: probability that every bin is not empty (h is onto)? Question: maximum number of balls in a bin (max{|h -1 (i)|})?

Birthday Problem Question:probability that each ball lands in its own bin (h is 1-1)? 1-》() m-1 This probability is some constant when m=(Vn) Jan 1st Jan 2nd Jan 3rd Jan 31st Feb 1st Dec 31st

Birthday Problem Question: probability that each ball lands in its own bin (h is 1-1)? Jan 1st Jan 2nd Jan 3rd Jan 31st Feb 1st … … Dec 31st This probability is some constant when

Coupon Collector Question:how many balls we need to throw to leave no empty bins? Let X;be the number of balls thrown until i bins are non-empty, given i-1 bins are already non-empty. X;is a geometric r.v.with parameter(n-i+1)/n. 公刘-X-店m-gn=m+o0m

Coupon Collector Question: probability that every bin is not empty (h is onto)? Question: how many balls we need to throw to leave no empty bins? … Let Xi be the number of balls thrown until i bins are non-empty, given i-1 bins are already non-empty. Xi is a geometric r.v. with parameter (n-i+1)/n

Load Balancing Question:maximum number of balls in a bin (maxh()? Let X;be the number of balls in bin i.That is,X=h(i). Let Y be i.r.v.taking value 1 iff ball j lands in bin i. E(Xi)=E m 1=1 Is maxE()}what we want? For every i,E()is m/n,so max E)is simply m/n. max{E(X,}= m

Load Balancing Question: maximum number of balls in a bin (max{|h -1 (i)|})? Let Xi be the number of balls in bin i. That is, Xi = |h -1 (i)|. Let Yij be i.r.v. taking value 1 iff ball j lands in bin i. Is max{𝔼(Xi )} what we want? For every i, 𝔼(Xi ) is m/n, so max{𝔼(Xi )} is simply m/n

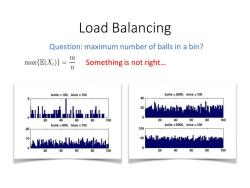
Load Balancing Question:maximum number of balls in a bin? 2X}-丹 Something is not right... balls =100,bins =100 balls =2000,bins =100 40 lhn山a 20 小w.oww 0 60 80 100 20 40 60 80 100 balls =600,bins =100 balls =5000,bins =100 20 100 10 Aar tbb s0klLuhuu 0 20 40 60 80 100 20 40 80 100

Load Balancing Question: maximum number of balls in a bin? Something is not right…

Load Balancing Question:maximum number of balls in a bin? When m=Θ(n): the max load is with high probability. When m =(nlog n): the max load is ()with high probability. with high probability (w.h.p.): We say an event happens with high probability(in n) if it happens with probability at least 1-1/n

Load Balancing with high probability (w.h.p.): We say an event happens with high probability (in n) if it happens with probability at least 1-1/n. Question: maximum number of balls in a bin?

Load Balancing When m=©(m): the max load is O logn log log n with high probability 13x≥0s20x≥0≤结 i=1 So we needP(X;≥t)≤ x≥≤（四）（月）（四）() =() InIn n esl let t=3In(n)/Inln(n) for sufficiently large n 31n2 n In n (elnlnlnn-InInn) ==e3nn+oa0）≤e-2h=

Load Balancing let m=n let t = 3ln(n)/lnln(n) for sufficiently large n

Load Balancing When m (nlogn): the max load is(with high probability P3:X≥0∑PX≥≤月 i=1 So we need P(Xi≥t)≤之 x≥≤(）()s()'() -()》= let t 4m/n 41g(n) 1

Load Balancing let m=nlg(n) let t = 4m/n = 4lg(n)

Load Balancing "m balls are thrown into n bins uniformly and independently at random" “uniformly at random choose h:[m]→[n" Question:maximum number of balls in a bin(maxh()? When m=Θ(n): the max load is with high probability When m =(nlog n): the max load is (with high probability

Load Balancing Question: maximum number of balls in a bin (max{|h -1 (i)|})? “m balls are thrown into n bins uniformly and independently at random” “uniformly at random choose h: [m]→[n]