南京大学：《高级算法 Advanced Algorithms》课程教学资源（课件讲稿）01 Introduction - Min-Cut and Max-Cut（尹⼀通）

Advanced Algorithms Introduction:Min-Cut and Max-Cut 尹-通Nanjing University,2022Fall

尹⼀通 Nanjing University, 2022 Fall Advanced Algorithms Introduction: Min-Cut and Max-Cut

Textbooks MIZED IMS Rajeev Motwani and Prabhakar Raghavan. Randomized Algorithms. Cambridge University Press,1995. VIJAY V.VAZIRANT Approximation Vijay Vazirani Algorithms Approximation Algorithms. Spinger-Verlag,2001

Textbooks Vijay Vazirani Approximation Algorithms. Spinger-Verlag, 2001. Rajeev Motwani and Prabhakar Raghavan. Randomized Algorithms. Cambridge University Press, 1995

References Probability and Mitzenmacher and Upfal. Computing Probability and Computing, in Alpethms and Data Anlysis 2nd Ed. and Eli Upfal The DESIGN of APPROXIMATION ALGORITHMS Williamson and Shmoys SECOND EDITION The Design of Approximation Algorithms Wiley Series in Discrete Mathematics and Optimizatlor Alon and Spencer The Probabilistic Method, Fourth Edition THE PROBABILISTIC 4th Ed. Clyorithms METHOD NOGA ALON-JOEL H.SPENCER DPV Sanjoy Dasgupta 房 Christos Papadimitriou Umesh Vaxirani Algorithms WILEY

References Mitzenmacher and Upfal. Probability and Computing, 2nd Ed. Williamson and Shmoys The Design of Approximation Algorithms Alon and Spencer The Probabilistic Method, 4th Ed. DPV Algorithms

Muhammad ibn Musa al-KhwarizmI (780-850) Advanced Algorithms

Advanced Algorithms Muḥammad ibn Mūsā al-Khwārizmī (780-850)

Minimum Cut

Minimum Cut

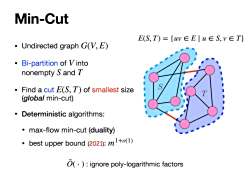
Min-Cut E(S,T)={uw∈E|u∈S,v∈T} Undirected graph G(V,E) Bi-partition of Vinto nonempty S and T Find a cut E(S,T)of smallest size (global min-cut) Deterministic algorithms: max-flow min-cut(duality) best upper bound (2021):m1+(1) O(.):ignore poly-logarithmic factors

Min-Cut • Undirected graph • Bi-partition of into nonempty and • Find a cut of smallest size (global min-cut) • Deterministic algorithms: • max-flow min-cut (duality) • best upper bound (2021): G(V, E) V S T E(S, T) m1+o(1) T S E(S, T) = {uv ∈ E ∣ u ∈ S, v ∈ T} : ignore poly-logarithmic factors O˜( ⋅ )

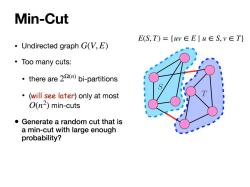
Min-Cut E(S,T)={uw∈E|u∈S,v∈T} Undirected graph G(V,E) ·Too many cuts: there are 29()bi-partitions ·(will see later）only at most O(n)min-cuts Generate a random cut that is a min-cut with large enough probability?

Min-Cut • Undirected graph • Too many cuts: • there are bi-partitions • (will see later) only at most min-cuts • Generate a random cut that is a min-cut with large enough probability? G(V, E) 2Ω(n) O(n2 ) T S E(S, T) = {uv ∈ E ∣ u ∈ S, v ∈ T}

Contraction Undirected multigraph GV,E) ·multigraph: ·allow parallel edges ·but no self-loop contract(e):e uv is an edge merges two endpoints u and v

Contraction • Undirected multigraph • multigraph: • allow parallel edges • but no self-loop • contract( ): is an edge • merges two endpoints and G(V, E) e e = uv u v e

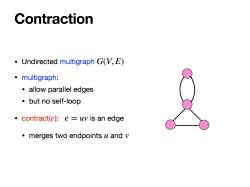
Contraction Undirected multigraph GV,E) 。multigraph: ·allow parallel edges ·but no self-loop contract(e):e uv is an edge merges two endpoints u and v

Contraction • Undirected multigraph • multigraph: • allow parallel edges • but no self-loop • contract( ): is an edge • merges two endpoints and G(V, E) e e = uv u v

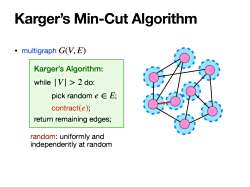
Karger's Min-Cut Algorithm ·multigraph G(V,E) Karger's Algorithm: whileV>2 do: pick random e∈E; contract(e); return remaining edges; random:uniformly and independently at random

Karger’s Algorithm: while do: pick random ; contract ; return remaining edges; |V| > 2 e ∈ E (e) • multigraph G(V, E) Karger’s Min-Cut Algorithm random: uniformly and independently at random