南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)10 Rounding Linear Programs

Advanced Algorithms Rounding Linear Program 尹一通Nanjing University,2022Fall
尹⼀通 Nanjing University, 2022 Fall Advanced Algorithms Rounding Linear Program

Vertex Cover
Vertex Cover
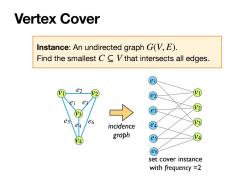
Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C V that intersects all edges. e2 e es e6 incidence graph V4 V4 set cover instance with frequency =2
Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V v1 v2 v3 v4 e1 e3 e2 e4 e1 e2 e3 e4 v1 v2 v3 e5 v4 e6 incidence graph set cover instance with frequency =2 e5 e6

Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C V that intersects all edges. ·NP-hard In(n)-approximation by greedy set cover 2-approximation algorithm: Find a maximal matching; return the matched vertices; .[Khot,Regev 2008]Assuming the unique games conjecture, there is no poly-time(2-e)-approximation algorithm
• NP-hard • -approximation by greedy set cover • 2-approximation algorithm: • [Khot, Regev 2008] Assuming the unique games conjecture, there is no poly-time -approximation algorithm. ln(n) (2 − ϵ) Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V Find a maximal matching; return the matched vertices;
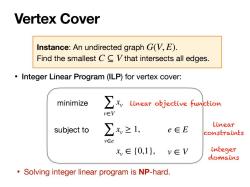
Vertex Cover Instance:An undirected graph G(V,E). Find the smallest CC Vthat intersects all edges. Integer Linear Program(ILP)for vertex cover: minimize ∑x linear objective function v∈V subject to ∑x≥1, Linear e∈E constraints v∈e x,∈{0,1},v∈V integer domains Solving integer linear program is NP-hard
• Integer Linear Program (ILP) for vertex cover: Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V linear objective function linear constraints integer domains • Solving integer linear program is NP-hard

Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C Vthat intersects all edges. Linear Program(LP)relaxation: minimize ∑x v∈V subject to ∑x≥1, e∈E v∈e x∈[0,1], v∈V fractional domains linear programs are solvable in polynomial time!
• Linear Program (LP) relaxation: Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V • linear programs are solvable in polynomial time! [ ] fractional domains

Linear Programming (LP) ·General form: matrix A={dijmxin],sets M [ml and NS [n] minimize cTx subject to afx =bi i∈M a,x≥b i∈M 光≥0 j∈N x;unconstrained j∈N
• General form: • matrix A = {a , sets and ij }[m]×[n] M ⊆ [m] N ⊆ [n] Linear Programming (LP) minimize subject to cTx aT i x = bi aT i x ≥ bi xj ≥ 0 xj unconstrained i ∈ M i ∈ M j ∈ N j ∈ N
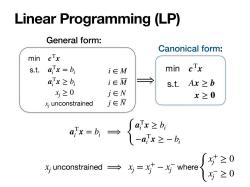
Linear Programming (LP) General form: Canonical form: min cTx s.t. ajx=b i∈M min cTx ax≥b, i∈M → s.t.Ax≥b 为≥0 j∈N x≥0 x;unconstrained j∈N -6-{的0 x;unconstrained→ 5咖e0 (七≥0
Linear Programming (LP) min s.t. cTx aT i x = bi aT i x ≥ bi xj ≥ 0 xj unconstrained i ∈ M i ∈ M j ∈ N j ∈ N General form: Canonical form: aT i x = bi ⟹ { aT i x ≥ bi −aT i x ≥ − bi x where j unconstrained ⟹ xj = x+ j − x− j { x+ j ≥ 0 x− j ≥ 0 ⟹ min s.t. cTx Ax ≥ b x ≥ 0
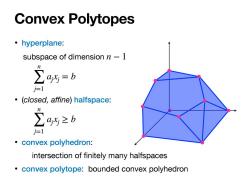
Convex Polytopes 。hyperplane: subspace of dimension n-1 ∑a45=b j=1 (closed,affine)halfspace: ∑a4y≥b j=1 。convex polyhedron: intersection of finitely many halfspaces convex polytope:bounded convex polyhedron
• hyperplane: subspace of dimension • (closed, affine) halfspace: • convex polyhedron: intersection of finitely many halfspaces • convex polytope: bounded convex polyhedron n − 1 n ∑ j=1 ajxj = b n ∑ j=1 ajxj ≥ b Convex Polytopes
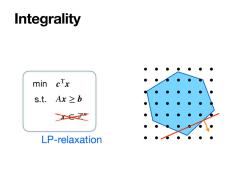
Integrality min cTx s.t.Ax≥b Z LP-relaxation
x ∈ ℤn Integrality min s.t. cTx Ax ≥ b LP-relaxation
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)09 Rounding Dynamic Programs.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)08 Greedy and Local Search.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)07 Lovász Local Lemma.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)06 Dimension Reduction.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)05 Concentration of measure.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)04 Hashing and Sketching.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)03 Balls into Bins.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)02 Fingerprinting.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)01 Introduction - Min-Cut and Max-Cut(尹⼀通).pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)03 Balls-into-Bins Model and Chernoff Bounds.pptx
- 《量子计算》课程教学资源(阅读文献)Lecture Notes on Quantum Algorithms(Andrew M. Childs).pdf
- 《量子计算》课程教学资源(阅读文献)Quantum Computation and Quantum Information(10th Anniversary Edition,Michael A. Nielsen & Isaac L. Chuang).pdf
- 《理论计算机科学》课程教学资源(阅读文献)Computational Complexity - A Modern Approach.pdf
- 《理论计算机科学》课程教学资源(阅读文献)Approximation via Correlation Decay when Strong Spatial Mixing Fails(HIS).pdf
- 《理论计算机科学》课程教学资源(阅读文献)Galton–Watson process - Branching.pdf
- 《理论计算机科学》课程教学资源(阅读文献)Analysis Of Boolean Functions(Ryan O’Donnell).pdf
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 14 假设检验.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 13 区间估计(参数估计).pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 12 点估计(参数估计).pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 11 统计量与抽样分布.pptx
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)11 The Primal-Dual Schema.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)12 SDP-Based Algorithms.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(教学大纲,杨春).pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)01 图论简介、图的定义及其相关概念、图的同构.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)02 完全图、偶图与补图、顶点的度与图的度序列.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)03 子图的相关概念、几种典型的图运算、路与连通性.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)04 图的代数表示、最短路算法.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)05 邻接谱、邻接代数与图空间、托兰定理.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)06 树的概念与应用、树的性质、树的中心与形心.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)07 生成树的概念与性质、生成树的计数、回路系统简介.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)08 克鲁斯克尔算法、管梅谷的破圈法、Prim算法、根树简介.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)09 图的连通性(割边、割点和块).pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)10 网络的容错性参数.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)11 图的宽直径简介.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)12 欧拉图与哈密尔顿图(欧拉图与中国邮路问题).pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)13 哈密尔顿图.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)14 度极大非哈密尔顿图与TSP问题.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)15 超哈密尔顿图与超可迹图问题.pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)16 匹配与因子分解(偶图的匹配问题).pdf
- 电子科技大学:《图论及其应用 Graph Theory and its Applications》研究生课程教学资源(课件讲稿)17 托特定理与图的因子分解.pdf
