电子科技大学：《图论及其应用 Graph Theory and its Applications》研究生课程教学资源（课件讲稿）03 子图的相关概念、几种典型的图运算、路与连通性

电子摊越女学 elveraityaf Bectrole Sclece and Techaology af Chaa 第一章图的基本概念 本次课内容 一、子图的相关概念 二、几种典型的图运算 三、路与连通性

第一章 图的基本概念 本次课内容 一、子图的相关概念 二、几种典型的图运算 三、路与连通性

电子科越女学 elveraity af Beetronle Sclence and Techaelogy af Cha /956 一、子图的相关概念 1、子图的概念 简单地说，图G的任意一非空部分（包括本身）都称为是图G的 的一个子图。定义如下： 定义1如果V(H)三V(G),E(H)sE(G), 且H中边的重数不超过G中对应边的条数，则称H为 G的子图，记为H三G 当 H三G,H≠G时，称H是G的真子图，记为 H

一、子图的相关概念 1、子图的概念 简单地说，图 G的任意一非空部分 (包括本身 )都称为是图 G 的 的一个子图。定义如下： 定义1 如果 ， 且H中边的重数不超过G中对应边的条数，则称H为 G的子图，记为 。 当 时，称H是G的真子图，记为

电子特越女学 veraitya Bectrole Sclece and TechaologyafChaa 1956 N3 N G V2 0 v3 V1 G1 69 G2

v 4 v 3 v 2 v1 v 4 v1 v 3 v 2 G 2 v1 G1 v1 v 4 G 3 G

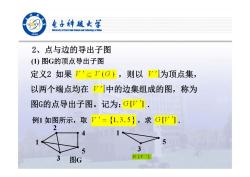
电子摊越女学 elveraity af Beetronle Sclence and Techaelogy af Cha 1956 2、点与边的导出子图 ()图G的顶点导出子图 定义2如果V'三V(G),则以V为顶点集， 以两个端点均在V刀中的边集组成的图，称为 图G的点导出子图。记为：G[V门 例1如图所示，取P'={1,3,5},求G[]. 2 5 3 3 图G GIV']

2、点与边的导出子图 (1) 图 G的顶点导出子图 定义2 如果 ，则以 为顶点集， 以两个端点均在 中的边集组成的图，称为 图G的点导出子图。记为： . 例1 如图所示，取 ，求 . 1 2 3 4 5 图 G G V[ ] 1 3 5

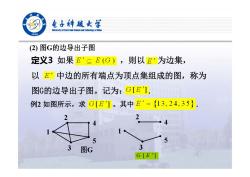
ST 电子摊越女学 elveraity af Beetronle Sclence and Techaelogy af Cha 1956 (2)图G的边导出子图 定义3如果E'三E(G),则以E'为边集， 以E”中边的所有端点为顶点集组成的图，称为 图G的边导出子图。记为：G[ET. 例2如图所示，求G[ET。其中E'={13,24,35} 2 5 5 3 图G 3 G[E']

(2) 图G的边导出子图 定义3 如果 ，则以 为边集， 以 中边的所有端点为顶点集组成的图，称为 图G的边导出子图。记为： . 例2 如图所示，求 。其中 . 1 2 3 4 5 图G G E[ ] 1 2 3 4 5

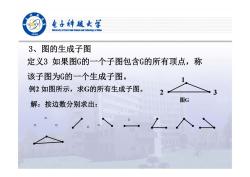
电子摊越女学 elveraity af Beetronle Sclence and Techaelogy af Cha /936 3、图的生成子图 定义3如果图G的一个子图包含G的所有顶点，称 该子图为G的一个生成子图。 例2如图所示，求G的所有生成子图。 ò3 解：按边数分别求出： 图G 。一

3、图的生成子图 定义3 如果图G的一个子图包含G的所有顶点，称 该子图为G的一个生成子图。 例2 如图所示，求G的所有生成子图。 1 2 3 图G 解：按边数分别求出：

电子摊越女学 elveraity af Beetronle Sclence and Techaelogy af Cha /956 定理1简单图G=(n,m)的所有生成子图个数为2m. 二、图运算 在图论中，将两个或更多的图按照某种方式合并，或者对 一个图作某种形式的操作，可以得到很有意义的新图。将图 合并或对一个图进行操作，称为图运算。图运算形式很多。 (一)、图的删点、删边运算 设V'三V(G), 在G中删去V"中的顶点和G中与之关联 的所有边的操作， 称为删点运算。记为G-P. 特别地，如果只删去一个点v,则记为G-V

定理1 简单图G=(n, m) 的所有生成子图个数为2m. 二、图运算 在图论中，将两个或更多的图按照某种方式合并，或者对 一个图作某种形式的操作，可以得到很有意义的新图。将图 合并或对一个图进行操作，称为图运算。图运算形式很多。 (一)、图的删点、删边运算 设 ，在G中删去 中的顶点和G中与之关联 的所有边的操作，称为删点运算。记为 . 特别地，如果只删去一个点v，则记为G-v

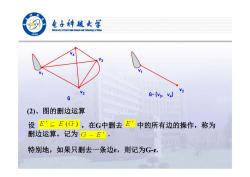
电子特越女学 elveraityaf Bectrole Sclece and Techaology af Chaa /936 V2 V2 G G-[v3,V4] (2)、图的删边运算 设E'三E(G),在G中删去 E'中的所有边的操作，称为 删边运算。记为G一E'· 特别地，如果只删去一条边e,则记为G-e

v4 v3 v2 v1 G v2 v1 G-{v3, v4} (2)、图的删边运算 设 ，在G中删去 中的所有边的操作，称为 删边运算。记为 . 特别地，如果只删去一条边e，则记为G-e

电子摊越女学 elveraityaf Bectrole Sclece and Techaology af Chaa 1956 e VA 。N4 c c 3 e6 es E5 G G-[e1,eg,e6,e5] 注：删点要删关联的边， 删边不删关联的点！ (二)、图的并运算 设G,G2是G的两个子图，G,与G,并是指由V(G1)UV(G2)为顶 点集，以E(G1)UE(G2)为边集组成的子图。记为：G1UG2

v1 v2 v3 v4 e1 e2 e3 e4 e5 e6 G G-{ e1, e3, e6, e5 } v1 v2 v3 v4 e2 e4 注：删点要删关联的边，删边不删关联的点！ (二)、图的并运算 设G1,G2是G的两个子图，G1与G2并是指由 为顶 点集，以 为边集组成的子图。记为：

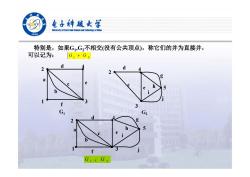
电子科越女学 elveraityaf Bectrole Sclece and Techaology af Chaa 1956 特别是，如果G,G,不相交（没有公共顶点）， 称它们的并为直接并， 可以记为： G1+G2 d d a e 3 f 3 G2 d 2 h a G1;G2

特别是，如果G1,G2不相交(没有公共顶点)，称它们的并为直接并， 可以记为： . 1 2 3 4 a b c d e f G1 h 2 3 5 4 c d e g i j G2 1 2 3 4 a b c d e f h 5 g i j G G 1 2 U