电子科技大学：《图论及其应用 Graph Theory and its Applications》研究生课程教学资源（课件讲稿）04 图的代数表示、最短路算法

电子科越女学 elveraityaf Bectrole Sclece and Techaology af Chaa 本次课内容 一、图的代数表示 二、最短路算法

本次课内容 一、图的代数表示 二、最短路算法

电子摊越女学 elveraity af Beetronle Sclence and Techaelogy af Cha /936 、 图的代数表示 在图论中，表示一个图主要有定义描述、图形表示和代数表示。 代数表示是用所谓邻接矩阵或关联矩阵来表示一个图。 (一)、图的邻接矩阵 1、定义1设G为n阶图，V={W1,V2,,V},邻接矩阵 A(G)=(a,其中： 1,v,与v间边数 ay 0,v,和v,不邻接

一、图的代数表示 在图论中，表示一个图主要有定义描述、图形表示和代数表示。 代数表示是用所谓邻接矩阵或关联矩阵来表示一个图。 ( 一 )、图的邻接矩阵 1、定义1 设 G 为 n阶图，V={v 1, v 2, …, v n}, 邻接矩阵 A(G)=(aij),其中：

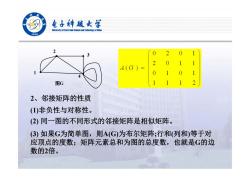
电子科越女学 elveraityaf Bectrole Sclece and Techaology af Chaa /936 2 3 2 A(G)= 图G 2、邻接矩阵的性质 ()非负性与对称性。 (2)同一图的不同形式的邻接矩阵是相似矩阵。 (3)如果G为简单图，则A(G)为布尔矩阵；行和（列和）等于对 应顶点的度数；矩阵元素总和为图的总度数，也就是G的边 数的2倍

1 2 3 4 图G 2、邻接矩阵的性质 (1)非负性与对称性。 (2) 同一图的不同形式的邻接矩阵是相似矩阵。 (3) 如果G为简单图，则A(G)为布尔矩阵;行和(列和)等于对 应顶点的度数；矩阵元素总和为图的总度数，也就是G的边 数的2倍

电子科越女学 elveraity af Beetronle Sclence and Techaelogy af Cha /956 (4)G连通的充分必要条件是：A(G)不能与如下矩阵相似： A22 证明：1)必要性： 若不然：设A对应的顶点是V1,V2,,Vk,A22对应的顶点 为Vk+1)Vk+2…,Vn0 显然，V(1≤i≤k)与v,(k+1≤i)不邻接，即G是非连通 图。矛盾！

(4) G连通的充分必要条件是：A(G)不能与如下矩阵相似： 证明：1) 必要性： 若不然：设A11对应的顶点是v1,v2,…, vk , A22对应的顶点 为vk+1,vk+2,…, vn。 显然，vi (1≤i≤k)与vj (k+1≤i≤n)不邻接，即G是非连通 图。矛盾！

电子科越女学 elveraity af Beetronle Sclence and Techaelogy af Cha /936 2)充分性 若不然：设G,与G,是G的两个不连通的部分，并且设 V(G)={V1V2,V,V(G2={Vk+1,Vk+2,Vn},如果在写 G的邻接矩阵时，先排V(G)中点，再排V(G2)中点，则G 的邻接矩阵形式必为： 这个性质说明：非连通图的邻接矩阵一定能够写成准 对角矩阵形式

2) 充分性 若不然：设G1与G2是G的两个不连通的部分，并且设 V(G1)={v1,v2,…,vk}, V(G2)={vk+1,vk+2,…,vn}, 如果在写 G的邻接矩阵时，先排V(G1)中点，再排V(G2)中点，则G 的邻接矩阵形式必为： 这个性质说明：非连通图的邻接矩阵一定能够写成准 对角矩阵形式

S) 电子科越女学 elvraity af Beetronle Sclece and Techaelogy af Chaa /956 (⑤)定理1设4*(G)=(a,,则a表示顶点v到顶点y的途径 长度为k的途径条数。 证明：对k作数学归纳法证明。 当k=1时，由邻接矩阵的定义，结论成立； 设结论对k-1时成立。当为k时： 一方面：先计算Ak. 4=4k-4=(a-a1+a (k-1a+ 2X2 另一方面：考虑v到y的长度为k的途径：

(5) 定理1 设 ，则a ij (k)表示顶点vi到顶点vj的途径 长度为k的途径条数。 证明：对k作数学归纳法证明。 当k=1时，由邻接矩阵的定义，结论成立； 设结论对k-1时成立。当为k时： 一方面：先计算Ak . 另一方面：考虑vi到vj的长度为k的途径:

电子摊越女学 elvraity af Beetronle Sclece and Techaelogy af Chaa /956 设ym是v到v的途径中点，且该点和v邻接。则v到v的经 过vm且长度为k的途径数目应该为： d(-d 所以，V到v的长度为k的途径数目为： -Da,1+a2- 02+…+ (k-1) 定理1得到证明。 如果G是简单图，我们得到如下推论： 推论：()A2的元素a:2是v,的度数，A3的元素a:3是含y 的三角形个数的2倍

设vm是vi到vj的途径中点，且该点和vj邻接。则vi到vj的经 过vm且长度为k的途径数目应该为： 所以，vi到vj的长度为k的途径数目为： 定理1得到证明。 如果G是简单图，我们得到如下推论： 推论: (1)A2的元素aii (2)是vi的度数，A3的元素aii (3)是含vi 的三角形个数的2倍

电子特越女学 elveraityaf Bectrole Sclece and Techaology af Chaa 1956 0 2 0 1 13 3 2 0 61 4 A(G)= 42(G)= 0 0 3 1 2 2 V2 V3 1 3 4 4 G 5 16 4 12 16 > 1012 A3(G)= 4 10 3 8 12 12 8 13 所以，V到v3的途径长度为2和3的条数分别为：3和4

v4 v1 v2 v3 G 所以，v1到v3的途径长度为2和3的条数分别为：3和4

电子摊越女学 Belveraity af Beetronle Sclence and Techaelogy af Chaa 1936 (二)、图的关联矩阵 1、定义2若G是(n,m)图。定义G的关联矩阵：M(G)=(a,)x 其中：a=1,y,与e,关联的次数(0,1，或2（环）) er V2 e2 110010 1 1 0 0 0 es e M(G)= 001 0 e 000112 0 e V3

(二)、图的关联矩阵 1、定义2 若G是(n, m) 图。定义G的关联矩阵： 其中： . e1 v4 v3 v v2 1 e7 e5 e4 e3 e2 e6 1100101 1110000 ( ) 0011001 0001120 M G               

ST 电子科越女学 elvraity af Beetronle Sclece and Techaelogy af Chaa /936 2、关联矩阵的性质 (1)关联矩阵的元素为0,1或2； (2)关联矩阵的每列和为2；每行的和为对应顶点度数， 二、最短路算法 (一)、几个相关概念 1、边赋权图 在图G的每条边e上赋予一个实数w(e)后，称G为边赋权图。 被标上的实数称为边的权值

2、 关联矩阵的性质 (1) 关联矩阵的元素为0，1或2； (2) 关联矩阵的每列和为2；每行的和为对应顶点度数. 二、最短路算法 (一)、几个相关概念 在图G的每条边e上赋予一个实数w (e)后, 称G为边赋权图。 被标上的实数称为边的权值。 1、 边赋权图