电子科技大学：《图论及其应用 Graph Theory and its Applications》研究生课程教学资源（课件讲稿）22 平面性算法

本次课主要内容 平面性算法 (一)、涉及算法的相关概念 (二)、平面性算法

0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 2 本次课主要内容 (一)、涉及算法的相关概念 (二)、平面性算法 平面性算法

(一)、涉及算法的相关概念 关于图的平面性问题，我们已经建立了一些平面性 判定方法： (1)对于简单图G=(n,m),如果m>3n-6,则G是非可 平面的； (2)对于简单连通图G=(m,),如果每个面次数至少 为23，且m>(m-2)11-2),则G是非可平面的； ③)库拉托斯基定理：G是可平面的当且仅当G不含有 与K和K3.3同胚的子图 (4)瓦格纳定理：G是可平面的当且仅当G不含有能够 收缩成K和K33的子图；

0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 3 关于图的平面性问题，我们已经建立了一些平面性 判定方法： (一)、涉及算法的相关概念 (1) 对于简单图G=(n, m)，如果m>3n-6，则G是非可 平面的； (2) 对于简单连通图G=(n, m)，如果每个面次数至少 为l≥3,且m>(n-2)l /(l-2)，则G是非可平面的； (3) 库拉托斯基定理：G是可平面的当且仅当G不含有 与K5和K3,3同胚的子图； (4) 瓦格纳定理：G是可平面的当且仅当G不含有能够 收缩成K5和K3,3的子图；

上面的判定方法，局限性很大。这次课我们将给出 一个算法，其作用是：如果G非可平面，通过算法可以 得到判定；如果G是可平面图，通过算法，可以给出一 种平面嵌入形式。 定义1设H是G的一个子图，在E(G)-E山中定义一 个二元关系“、”： e,e,∈E(G)-E(H,ee,当且仅当存在一条途径W,使得： (I)e,与e2分别是W的始边和终边，且 (2)W的内点与H不能相交。 e e

0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 4 上面的判定方法，局限性很大。这次课我们将给出 一个算法，其作用是：如果G非可平面，通过算法可以 得到判定；如果G是可平面图，通过算法，可以给出一 种平面嵌入形式。 定义1 设H是G的一个子图，在E(G)-E(H)中定义一 个二元关系“ ~”: 12 1 2   e e EG EH e e , ( ) ( ), 当且仅当存在一条途径W,使得： (1) e1与e2分别是W的始边和终边，且 (2) W的内点与H不能相交。 G e4 e3 e2 e1 e7 e6 e5

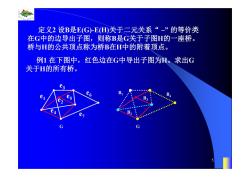
定义2设B是E(G)-E山D关于二元关系“”的等价类 在G中的边导出子图，则称B是G关于子图的一座桥。 桥与H的公共顶点称为桥B在H中的附着顶点。 例1在下图中，红色边在G中导出子图为H。求出G 关于H的所有桥。 e e 4

0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 5 定义2 设B是E(G)-E(H)关于二元关系“ ~” 的等价类 在G中的边导出子图，则称B是G关于子图H的一座桥。 桥与H的公共顶点称为桥B在H中的附着顶点。 例1 在下图中，红色边在G中导出子图为H。求出G 关于H的所有桥。 G B1 B2 B3 B4 G e4 e3 e2 e1 e7 e6 e5

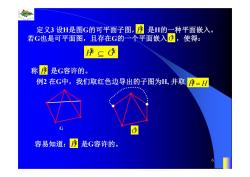
定义3设H是图G的可平面子图，序是H的一种平面嵌入。 若G也是可平面图，且存在G的一个平面嵌入，使得： 称序 是G容许的。 例2在G中，我们取红色边导出的子图为H,并取序=H 容易知道：序是G容许的

0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 6 定义3 设H是图G的可平面子图， 是H的一种平面嵌入。 若G也是可平面图，且存在G的一个平面嵌入 ，使得： 称 是G容许的。 H% G% H G %  % H% 例2 在G中，我们取红色边导出的子图为H, 并取 H% H 容易知道： 是G容许的。 G G% H%

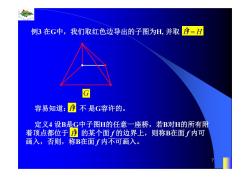
例3在G中，我们取红色边导出的子图为H,并取 序=H G 容易知道：序不是G容许的。 定义4设B是G中子图H的任意一座桥，若B对H的所有附 着顶点都位于序的某个面f的边界上，则称在面f内可 画入，否则，称B在面f内不可画入

0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 7 例3 在G中，我们取红色边导出的子图为H, 并取 H% H 容易知道： 不 是G容许的。 G H% 定义4 设B是G中子图H的任意一座桥，若B对H的所有附 着顶点都位于 的某个面 f 的边界上，则称B在面 f 内可 画入，否则，称B在面 f 内不可画入。 H%

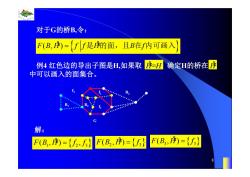
对于G的桥B,令： F(B,)={//是的面，且B在内可画入》 例4红色边的导出子图是H,如果取序=H 确定H的桥在序 中可以画入的面集合。 G 解： F(B,序={，} F(B2,净)={f} F(B,={f} 8

0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 8 对于G的桥B,令： 例4 红色边的导出子图是H,如果取 确定H的桥在 中可以画入的面集合。 FBH f f H B f (, )    % % 是 的面，且 在 内可画入 H%=H H% B3 B1 B2 f3 f2 f1 G F(,) , BH f f 1 23    % 解： F(,) BH f 2 3    % F(,) BH f 3 3    %

定理1设序 是G容许的，则对于H的每座桥B: F(B,序)≠Φ 证明：因序是G容许的，由定义，存在G的一个平面嵌 入ě，使得： 序 于是，H的桥B所对应的帝 的子图，必然限制在序的 某个面内。所以： F(B,序)≠Φ 注：定理1实际上给出了一个图是可平面图的一个必要条 件。这个必要条件表明：如果存在G的一个可平面子图H

0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 9 定理1 设 是 H% G容许的，则对于H的每座桥B: FBH (, ) %   证明：因 是G容许的，由定义，存在G的一个平面嵌 入 ，使得： H% G% H%  G% 于是，H的桥B所对应的 的子图，必然限制在 的 某个面内。所以： G% H% FBH (, ) %   注：定理1实际上给出了一个图是可平面图的一个必要条 件。这个必要条件表明：如果存在G的一个可平面子图H

使得对于某桥B,有F(B,)=D,那么，G是非 可平面的。 根据上面的结论：我们可以按如下方式来考虑G 的平面性问题： 先取G的一个可平面子图H,其平面嵌入是序 对于H的每座桥B,如果：F(B,序)=Φ，则G非可 平面。 否则，取H的桥B1,作：H2=B,UH1,再取一个面 f∈F(B,房) 将B画入序的面f中。 10

0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 10 使得对于某桥B，有 ，那么，G是非 可平面的。 FBH ( , )= %  根据上面的结论：我们可以按如下方式来考虑G 的平面性问题： 先取G的一个可平面子图H1, 其平面嵌入是 H1 % 对于H1的每座桥B,如果： ，则G非可 平面。 1 FBH ( , )= %  否则，取H1的桥B1,作：H2=B1∪H1,再取一个面 1 1 f  FB H (, ) % 将B1画入 的面 H%1 f 中

如果B可平面，则只要把B平面嵌入后，得到H的 平面嵌入序， 然后再进行上面相同的操作，可以得到G的边数 递增的子图平面嵌入序列： 序，序6 最终，得到可平面图G的一种平面嵌入形式。 (二)、平面性算法 1964年，德穆克龙Demoucron),莫尔根思Mlgrance和 珀特维斯(Pertuiset)提出了下面的平面性算法，简称DMP 算法

0.8 1 0.6 0.4 0.2 0 x t 0 0.5 1 1.5 2 1 0.5 0 0.5 1 n 11 如果B1可平面，则只要把B1平面嵌入后，得到H2的 平面嵌入 然后再进行上面相同的操作，可以得到G的边数 递增的子图平面嵌入序列： 1 2 H H % %, L 最终，得到可平面图G的一种平面嵌入形式。 H2 % (二)、平面性算法 1964年，德穆克龙(Demoucron), 莫尔根思(Mlgrance)和 珀特维斯(Pertuiset)提出了下面的平面性算法，简称DMP 算法