南京大学：《概率论与数理统计 Probability and Statistics》课程教学资源（PPT课件讲稿）Lecture 13 区间估计（参数估计）

参数估计

参数估计

提纲 2 口矩估计(The Method of Moments) 口极大仪然估计The Method of Maximum Likelihood)》 口估计量的评选标准 口区间估计

提纲  矩估计(The Method of Moments)  极大似然估计（The Method of Maximum Likelihood）  估计量的评选标准  区间估计 2

内容 3 口基本概念与枢轴变量法 ▣正态总体情形 口双正态总体情形 ▣单侧置信区间 ▣非正态总体均值的区间估计

内容  基本概念与枢轴变量法  正态总体情形  双正态总体情形  单侧置信区间  非正态总体均值的区间估计 3

区间估计 4 区间估计：根据样本给出未知参数0 的一个范围（⑥，02），并保证这个范围以 较大概率包含参数真值，即： P(⑥，(X,X2,L,Xm)<0<02(X1,X,L,Xn)=1-a

区间估计 4 区间估计：根据样本给出未知参数θ 的一个范围 ，并保证这个范围以 较大概率包含参数真值，即： θ θ 1 1 2 2 1 2 ˆ ˆ ( ( , , , ) ( , , , )) 1 P X X X X X X n n L L   = −   θ θ 1 2 ˆ ˆ ( , )

置信区间与置信度 5 定义：设总体X含未知参数0；对于样本 X1,L,Xn,找出统计量： 0=0,(X,L,Xm)(i=1,2),日<6，使得： P0≤0≤0，}=1-，(0<a<1) 称区间[⊙，0，]为的置信区间，1-a为该 区间的置信度

置信区间与置信度 5 1 1 1 2 , , , ˆ ˆ ˆ ( , , ) ( 1,2), , = =  n i i n X X X X X i      定义：设总体 含未知参数 ；对于样本 找出统计量: 使得： L L 1 2 ˆ ˆ P{ } 1 , (0 1)        = −   1 2 ˆ ˆ [ ] 1 称区间    ， 为 的置信区间，− 为该 区间的置信度

6 区间[0,0，]是一个随机区间：l-a给出 该区间含真值的可靠程度。表示该☒ 间不包含真值的可能性。 例如：若a=5%,即置信度为1-α=95%.重 复抽样100次，得到100个区间，其中包含0真 值的有95个左右，不包含0真值的有5个左右 通常，采用95%的置信度，有时也取99%或90%

6 1 2 ˆ ˆ [ ] 1       区间 ， 是一个随机区间；− 给出 该区间含真值 的可靠程度。 表示该区 间不包含真值 的可能性。 5% 1 95%. 100 100 95 5     例如：若 = − = ，即置信度为 重 复抽样 次，得到 个区间，其中包含 真 值的有 个左右，不包含 真值的有 个左右。 通常，采用95%的置信度，有时也取99%或90%

几点说明 1.置信区间的长度L反映了估计精度， L越小，估计精度越高 2.反映了估计的可靠度，越小，越可靠 0越小，1-越大，估计的可靠度越高，但 这时，L往往增大，因而估计精度降低： 3.确定后，置信区间的选取方法不唯一， 常选长度最小的一个

几点说明 7 2.  反映了估计的可靠度,  越小, 越可靠. 1. 置信区间的长度L 反映了估计精度,  越小, 1-  越大, 估计的可靠度越高,但 3.  确定后, 置信区间 的选取方法不唯一, 常选长度最小的一个. L 越小, 估计精度越高. 这时, L 往往增大, 因而估计精度降低

枢轴变量法 8 1.先找到一样本函数U(X1,X2,…,Xni0), 其包含待估参数0，而不包含其他未知 参数，且U的分布已知，不依赖于任何 未知参数。U被称为枢轴变量。 2.给定置信度1一，根据U的分布找2个 常数a和b,使得P(a<U<b)=1-a 3.由a<U≤b解出01<0<02，则 01,02)为所求置信区间

枢轴变量法 8 1. 先找到一样本函数𝑼(𝑿𝟏,𝑿𝟐,… ,𝑿𝒏;𝜽), 其包含待估参数𝜽，而不包含其他未知 参数，且𝑼的分布已知，不依赖于任何 未知参数。𝑼被称为枢轴变量。 2. 给定置信度𝟏 − 𝜶，根据𝑼的分布找2个 常数𝒂和𝒃，使得𝑷 𝒂 < 𝑼 < 𝒃 = 𝟏 − 𝜶 3. 由𝒂 < 𝑼 < 𝒃解出𝜽 ෡ 𝟏 < 𝜽 < 𝜽 ෡ 𝟐，则 (𝜽 ෡ 𝟏,𝜽 ෡ 𝟐)为所求置信区间

正态总体，均值的μ区间估计 9 设X,…,X,n为总体X~N(4,o2)的一个样本。 在置信度1-a下，来确定的置信区间[0,02] ().已知方差，估计均值 设已方羞。2=.则=。 -4~N(0,1 o 对于给定的置信度1-α，查正态分布表，找出临界 值2，元2，使得： P{2≤U≤元2}=1-x

正态总体，均值的μ区间估计 9 2 1 1 2 , , ~ ( , ) 1 [ ] X X X N n   −    设 为总体 的一个样本。 在置信度 下，来确定 的置信区间 ， 。 (1). 已知方差，估计均值 2 2 0 0 , ~ (0,1) / X U N n     − 设已知方差 = = 则 。 1 2 1 2 1 : { } 1 . P U       −   = − 对于给定的置信度 ，查正态分布表，找出临界 值 ， ，使得

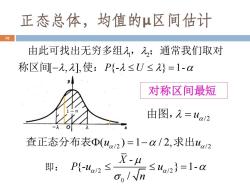
正态总体，均值的μ区间估计 10 由此可找出无穷多组2，入；通常我们取对 称区间[-九，]，使：P{-九≤U≤}=1- 对称区间最短 由图，人=ua2 查正态分布表Φ(u2)=1-a/2,求出a/2 X-u 即：P叭w:n≤a=l-a

正态总体，均值的μ区间估计 10 1 2 [ , ], {- } 1- P U   −   =      由此可找出无穷多组 ， ；通常我们取对 称区间 使： 即： /2 /2 0 - {- } 1- / X P u u n        = 对称区间最短 / 2 u 由图， =  /2 /2 ( ) 1 / 2, u u 查正态分布表 = −    求出