南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 23 树的基本概念

1 树的基本概念
树的基本概念 1

回顾 口问题1:什么是二部图及其匹配? ▣两个无内部边的顶点集;互不相邻的边的集合 口问题2:二部图中的有哪些匹配? 口完备匹配:一个部饱和,充要条件为Hal定理 口最大匹配:充要条件为无增广路径(Berge定理) ▣稳定匹配:每个节点有线性序,稳定匹配算法
问题1:什么是二部图及其匹配? 两个无内部边的顶点集;互不相邻的边的集合 问题2:二部图中的有哪些匹配? 完备匹配:一个部饱和,充要条件为Hall定理 最大匹配:充要条件为无增广路径(Berge定理) 稳定匹配:每个节点有线性序,稳定匹配算法 回顾

本节提要 口内容1:树的定义及其性质 ▣内容2:根树以及有序根树的遍历
内容1:树的定义及其性质 内容2:根树以及有序根树的遍历 本节提要
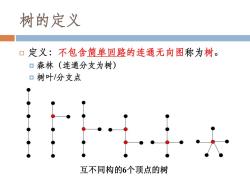
树的定义 口定义:不包含简单回路的连通无向图称为树。 口森林(连通分支为树) ▣树叶/分支点 互不同构的6个顶点的树
树的定义 定义:不包含简单回路的连通无向图称为树。 森林(连通分支为树) 树叶/分支点 互不同构的6个顶点的树
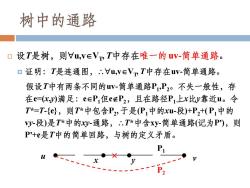
树中的通路 设T是树,则u,V∈VT中存在唯一的uV-简单通路。 口证明:T是连通图,.u,V∈VvT中存在uv-简单通路。 假设T中有两条不同的uV-简单通路P1,P2。不失一般性,存 在e=(cy)满足:e∈P1但eP2,且在路径P1上x比y靠近u。令 T*=T-{e},则T*中包含P2,于是(P1中的xu-段)+P2+(P1中的 Vy-段)是T*中的y-通路,.T*中含xy-简单通路(记为P),则 P+是T中的简单回路,与树的定义矛盾。 -。、 X
设T是树,则u,vVT , T中存在唯一的uv-简单通路。 证明:T是连通图,u,vVT , T中存在uv-简单通路。 假设T中有两条不同的uv-简单通路P1 ,P2。不失一般性,存 在e=(x,y)满足:eP1但eP2,且在路径P1上x比y靠近u。令 T*=T-{e},则T*中包含P2 , 于是(P1中的xu-段)+P2+( P1中的 vy-段)是T*中的xy-通路,T*中含xy-简单通路(记为P’),则 P’+e是T中的简单回路,与树的定义矛盾。 u x y v P2 P1 树中的通路

有关树的几个等价命题 口设T是简单无向图,下列四个命题等价: (1)T是不包含简单回路的连通图。树的定义 (2)T中任意两点之间有唯一简单通路。 (3)T连通,但删除任意一条边则不再连通。 (4)T不包含简单回路,但在任意不相邻的顶点对之间加一 条边则产生唯一的简单回路。 口备注: ■树是边最少的连通图 ■树是边最多的无简单回路的图
设T是简单无向图,下列四个命题等价: (1) T是不包含简单回路的连通图。//树的定义 (2) T中任意两点之间有唯一简单通路。 (3) T连通,但删除任意一条边则不再连通。 (4) T不包含简单回路,但在任意不相邻的顶点对之间加一 条边则产生唯一的简单回路。 备注: ◼ 树是边最少的连通图 ◼ 树是边最多的无简单回路的图 有关树的几个等价命题

树中边和点的数量关系 设T是树,令n=Vbm=ET,则Fn-I。 口证明.对n进行归纳证明。当n=1,T是平凡树,结论显然成立。 假设当n≤k时结论成立。 若n=k+1。因为T中每条边都是割边,任取e∈ET-{e}含两 个连通分支,设其为T1,T2,并设它们边数分别是m1,m2, 顶点数分别是n1,2,根据归纳假设:m11,m2=21。 注意:n+n2=n,m1+m2=m-1。 ∴.m=m+m2+1=n-1
设T是树,令n=|VT |, m=|ET |, 则m=n-1。 证明. 对n进行归纳证明。当n=1, T是平凡树,结论显然成立。 假设当nk时结论成立。 若n=k+1。因为T中每条边都是割边,任取eET , T-{e}含两 个连通分支,设其为T1 , T2 , 并设它们边数分别是m1 , m2 , 顶点数分别是n1 , n2 , 根据归纳假设:m1=n1 -1, m2=n2 -1。 注意:n1+n2=n, m1+m2=m-1。 m= m1+m2+1=n-1。 树中边和点的数量关系

连通图边数的下限 口顶点数为n(n≥2)的连通图,其边数m2-1。 (对于树,=n-L,“树是边最少的连通图”) 口证明:对n进行一般归纳。当n=2时结论显然成立。 设G是边数为m的连通图,且IVc=n>2。任取veVc,令 G=G-y,设G有@(@≥1)个连通分支G1,G2,,G。,且G的边 数和顶点数分别是m和no 我们有n=n1+n2+..+n。+1,m≥m1+m2+..+m。+o(每个连通 分支中至少有一个顶点在G中与删除的相邻)。 由归纳假设,m≥n-1(=1,2,.w)。 所以:m2m1+m2+..+mo十o之n+n2+..+no0+0=n-1o
顶点数为n(n2)的连通图,其边数mn-1。 (对于树,m=n-1, “树是边最少的连通图”) 证明:对n进行一般归纳。当n=2时结论显然成立。 设G是边数为m的连通图,且|VG |=n>2。任取vVG,令 G’=G-v,设G’有(1)个连通分支G1 ,G2 ,…,G,且Gi的边 数和顶点数分别是mi和ni。 我们有n=n1+n2+…+n +1, mm1+m2+…+m + (每个连通 分支中至少有一个顶点在G中与删除的v相邻)。 由归纳假设,mi ni -1(i=1,2,…)。 所以:m m1+m2+…+m +n1+n2+…+n -+=n-1。 连通图边数的下限

与边点数量关系有关的等价命题 设T是简单无向图,下列三个命题等价: (1)T是树。 (2)T不含简单回路,且m=n-1。 (3)T连通,且m=n-1。 口(1)→(2),已证。 口(2)→(3),若不连通,分支数四≥2,各分支为树(无简单回 路、连通),则m=n-o<n-1,矛盾。 口(3)→(I),设e是T中任意一条边,令T'=T-e,且其边数和顶点 数分别是m'和n,则m’=m-1=n-2<n-1,∴.T是非连通图。因 此,G的任意边均不在简单回路中,G中无简单回路
设T是简单无向图,下列三个命题等价: (1) T是树。 (2) T不含简单回路,且m=n-1。 (3) T连通,且m=n-1。 (1)(2), 已证。 (2)(3), 若不连通,分支数2,各分支为树(无简单回 路、连通),则m=n-<n-1,矛盾。 (3)(1), 设e是T中任意一条边,令T’=T-e, 且其边数和顶点 数分别是m’和n, 则m’=m-1=n-2<n-1, T’是非连通图。因 此,G的任意边均不在简单回路中,G中无简单回路。 与边点数量关系有关的等价命题

本节提要 口内容1:树的定义及其性质 口树就是不包含简单回路的连通无向图 口树是边最少的连通图;也是边最多的无简单回路的图 口内容2:根树以及有序根树的遍历
内容1:树的定义及其性质 树就是不包含简单回路的连通无向图 树是边最少的连通图;也是边最多的无简单回路的图 内容2:根树以及有序根树的遍历 本节提要
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 22 二部图与匹配.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 21 最短通路问题.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 20 欧拉图与汉密尔顿图.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 19 图的连通性.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 18 图论基本概念.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 17 布尔代数.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 16 代数格.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 15 循环群与群同构.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 14 子群及其陪集.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 13 群伦导引.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 12 等价关系与偏序关系.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 11 关系的性质.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 10 离散概率.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 09 计数.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 08 归纳与递归.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 07 数论基础.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 06 集合的基数.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 05 关系与函数.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 04 集合及其运算.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 03 证明方法.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 24 树的应用.pptx
- 南京大学:《离散数学》课程教学资源(PPT课件讲稿)Lecture 25 生成树.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 01 引言、概率论基本概念、古典概型.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 02 几何概型、条件概率与独立性.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 03 离散型随机变量.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 04 几个典型的离散型随机变量.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 05 条件期望、方差.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 06 概率化方法(主讲:唐斌).pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 07 连续型随机变量.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 08 典型连续型随机变量的分布.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 09 典型二维连续型随机变量、相关系数.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 10 极限理论.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 11 统计量与抽样分布.pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 12 点估计(参数估计).pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 13 区间估计(参数估计).pptx
- 南京大学:《概率论与数理统计 Probability and Statistics》课程教学资源(PPT课件讲稿)Lecture 14 假设检验.pptx
- 《理论计算机科学》课程教学资源(阅读文献)Analysis Of Boolean Functions(Ryan O’Donnell).pdf
- 《理论计算机科学》课程教学资源(阅读文献)Galton–Watson process - Branching.pdf
- 《理论计算机科学》课程教学资源(阅读文献)Approximation via Correlation Decay when Strong Spatial Mixing Fails(HIS).pdf
- 《理论计算机科学》课程教学资源(阅读文献)Computational Complexity - A Modern Approach.pdf
