南京大学：《离散数学》课程教学资源（PPT课件讲稿）Lecture 14 子群及其陪集

1 子群及其陪集

子群及其陪集 1

回顾 2 口问题1：什么是代数系统？ 口非空集合+封闭的（二元）运算 口问题2：代数系统相关性质？ 口封闭性、结合性、交换性、分配性；单位元、零元、逆 元；同态同构 口问题3：什么是群？ 口封闭+结合律+单位元+逆元 口问题4：群具有哪些性质？ ▣元素的阶、群的阶

回顾  问题1：什么是代数系统？  非空集合+封闭的(二元)运算  问题2：代数系统相关性质？  封闭性、结合性、交换性、分配性；单位元、零元、逆 元；同态同构  问题3：什么是群？  封闭 + 结合律 + 单位元 + 逆元  问题4：群具有哪些性质？  元素的阶、群的阶 2

本节提要 3 口问题1：什么是子群，如何判别之？ ▣问题2：子群一定存在么，若存在则满足什 么性质？

本节提要  问题1：什么是子群，如何判别之？  问题2：子群一定存在么，若存在则满足什 么性质？ 3

子群的定义 4 口设(G,o)是群，H是G的非空子集，如果H关于G中 的运算构成群，即(H,)也是群，则H是G的子群。 口记作(H,)≤(G,),简记为H≤G。 口例子：偶数加系统是整数加群的子群 o平凡子群(G,o),({e},o) 注意：结合律在G的子集上均成立

子群的定义  设(G, ⃘)是群，H是G的非空子集，如果H关于G中 的运算构成群，即(H, ⃘)也是群，则H是G的子群。  记作(H, ⃘)  (G, ⃘), 简记为 HG。  例子：偶数加系统是整数加群的子群  平凡子群 (G, ⃘)， ({e}, ⃘) 注意：结合律在G的子集上均成立。 4

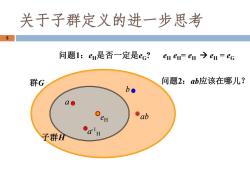
关于子群定义的进一步思考 5 问题1：eH是否一定是ec? en en=en→eH=eG 群G 问题2：ab应该在哪儿？ b● ao 。w ab 子群A Oa'H

群G 子群H a b eH a -1 H 问题2：ab应该在哪儿？ ab 问题1：eH是否一定是eG? eH eH = eH → eH = eG 5 关于子群定义的进一步思考

子群的判定：判定定理一 6 0 G是群，H是G的非空子集。H是G的子群当且仅 当： aVa,b∈H,ab∈H,并且 ▣Va∈H,al∈H (注意：这里是a在G中的逆元，当H确定为群后，它也是a在H中的逆元) 口证明 口必要性显然 口充分性：只须证明G中的单位元也一定在H中，它即 是H的单位元素

 G是群，H是G的非空子集。H是G的子群当且仅 当：  a,bH, abH, 并且  aH, a -1H （注意：这里a -1是a在G中的逆元，当H确定为群后，它也是a在H中的逆元）  证明  必要性显然  充分性：只须证明G中的单位元也一定在H中，它即 是H的单位元素。 6 子群的判定：判定定理一

子群的判定：判定定理二 口G是群，H是G的非空子集。H是G的子群当且仅当： Va,b∈Hab1eH 口证明 口必要性易见 口充分性： ■单位元素：因为H非空，任取M∈H,e=心l∈H ■逆元素：Va∈H,因为e∈H,所以心l=el∈H ■封闭性：Va,b∈H,已证b-1∈H,所以ab=(b11∈H

 G是群，H是G的非空子集。H是G的子群当且仅当： a,bH, ab-1H  证明  必要性易见  充分性： ◼ 单位元素：因为H非空，任取aH, e=aa-1H ◼ 逆元素：aH, 因为eH, 所以 a -1=ea-1H ◼ 封闭性：a,bH, 已证b -1H，所以ab=a(b -1 ) -1H 7 子群的判定：判定定理二

子群的判定：判定定理三 8 G是群，H是G的非空有限子集。H是G的子群当且仅当： Va,b∈H,ab∈H 口证明.必要性显然.下证充分性，只须证明逆元素性 ■若H中只含G的单位元，H显然是子群。 ■否则，任取H中异于单位元的元素考虑序列 ,2,,… 注意：该序列中各项均为有限集合H中的元素，因此， 必有正整数i,jGj>i,满足：=心，由消去率有e=i,因 此： ml=d1∈H

 G是群，H是G的非空有限子集。H是G的子群当且仅当： a,bH, abH  证明. 必要性显然. 下证充分性，只须证明逆元素性 ◼ 若H中只含G的单位元，H显然是子群。 ◼ 否则，任取H中异于单位元的元素a, 考虑序列 a, a 2 , a 3 , ... 注意：该序列中各项均为有限集合H中的元素，因此， 必有正整数i, j(j>i), 满足：a i=a j ,由消去率有e=a j-i，因 此： a -1=a j-i-1 H 8 子群的判定：判定定理三

本节提要 9 口问题1：什么是子群，如何判别之？ 口非空子集+封闭、结合律、单位元、逆元 口判定：根据定义或三个判定定理 口问题2：子群一定存在么，若存在则满足什 么性质？

本节提要  问题1：什么是子群，如何判别之？ 非空子集 + 封闭、结合律、单位元、逆元 判定：根据定义或三个判定定理  问题2：子群一定存在么，若存在则满足什 么性质？ 9

生成子群 10 口设G是群，M∈G,构造G的子集H如下： H={ak|k是整数} 则H构成G的子群，称为生成的子群(） 口证明： oH非空：M在H中 口利用判定定理二： Vam,"∈H,m(a)-1=m-n∈H 非平凡子群一定存在么？

 设G是群，aG，构造G的子集H如下： H = {a k | k是整数 } 则H构成G的子群，称为a生成的子群 〈a〉  证明：  H非空：a在H中 利用判定定理二： a m ,a nH, a m(a n ) –1 =a m-nH 10 生成子群 非平凡子群一定存在么？