电子科技大学：《矩阵理论 Matrix Theory》课程教学资源（课件讲稿）05 Special matrices-matlab

Matrix Theory -Special Matrices School of Mathematical Sciences Teaching Group Main Reference books Fuzhen Zhang.Matrix Theory-Basic Results and Techniques,Second Edition. Springer,2011. llse C.F.Ipsen,Numerical Matrix Analysis:Linear Systems and Least Squares.SIAM.2009. Reference books: Roger A.Horn and Charles A.Johnson:Matrix Analysis.Cambridge University Press,1985. Gene H.Golub and Charles F.Van Loan:Matrix Computations,Third Edition.Johns Hopkins Press,1996. Nicholas J.Higham.Accuracy and Stability of Numerical Algorithms,Second Edition.SIAM,2002. Y.Saad.Iterative Methods for Sparse Linear Systems,Second Edition. SIAM Philadelphia2003. Maintained by Yan-Fei Jing

: Main Reference books ▸ Fuzhen Zhang. Matrix Theory-Basic Results and Techniques, Second Edition. Springer, 2011. ▸ Ilse C. F. Ipsen, Numerical Matrix Analysis: Linear Systems and Least Squares. SIAM, 2009. Reference books: ▸ Roger A. Horn and Charles A. Johnson: Matrix Analysis. Cambridge University Press, 1985. ▸ Gene H. Golub and Charles F. Van Loan: Matrix Computations, Third Edition. Johns Hopkins Press, 1996. ▸ Nicholas J. Higham. Accuracy and Stability of Numerical Algorithms, Second Edition. SIAM, 2002. ▸ Y. Saad. Iterative Methods for Sparse Linear Systems, Second Edition. SIAM, Philadelphia, 2003. Maintained by Yan-Fei Jing Matrix Theory ––Special Matrices School of Mathematical Sciences Teaching Group Matrix Theory Special Matrices

Hilbert Matrix Outline Hilbert Matrix Circulant Matrix Toeplitz Matrix Hankel Matrix Vandermonde Matrix Summary Questions Extensive reading 奇老有这女习 Matrix Theory Matrices -2/29

Hilbert Matrix Outline Hilbert Matrix Circulant Matrix Toeplitz Matrix Hankel Matrix Vandermonde Matrix Summary & Questions Extensive reading Matrix Theory Matrices - 2/29

Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position(i,j)is l≤i,j≤n,is called a Hilbert matrix. 命电有这女 Matrix Theory Matrices -3/29

Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position (i, j) is 1 i+j−1 , 1 ≤ i, j ≤ n, is called a Hilbert matrix. Write down a Hilbert matrix for n = 5. MATLAB command: hilb ▸ hilb(n) is the n × n (n-square) matrix with elements 1 i+j−1 , which is a famous example of a badly conditioned matrix. See INVHILB for the exact inverse. ▸ the exact inverse: invhilb(n) is the inverse of the n-square matrix with elements 1 i+j−1 . ▸ The result is exact for n less than about 15. Matrix Theory Matrices - 3/29

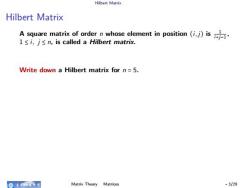
Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position(i,j)is l≤i,j≤n,is called a Hilbert matrix. Write down a Hilbert matrix for n=5. 奇电有这头 Matrix Theory Matrices -3/29

Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position (i, j) is 1 i+j−1 , 1 ≤ i, j ≤ n, is called a Hilbert matrix. Write down a Hilbert matrix for n = 5. MATLAB command: hilb ▸ hilb(n) is the n × n (n-square) matrix with elements 1 i+j−1 , which is a famous example of a badly conditioned matrix. See INVHILB for the exact inverse. ▸ the exact inverse: invhilb(n) is the inverse of the n-square matrix with elements 1 i+j−1 . ▸ The result is exact for n less than about 15. Matrix Theory Matrices - 3/29

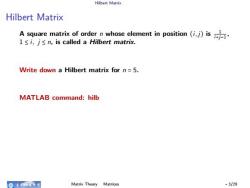
Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position (i,j)is l≤i,j≤n,is called a Hilbert matrix. Write down a Hilbert matrix for n=5. MATLAB command:hilb 奇电有这头 Matrix Theory Matrices -3/29

Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position (i, j) is 1 i+j−1 , 1 ≤ i, j ≤ n, is called a Hilbert matrix. Write down a Hilbert matrix for n = 5. MATLAB command: hilb ▸ hilb(n) is the n × n (n-square) matrix with elements 1 i+j−1 , which is a famous example of a badly conditioned matrix. See INVHILB for the exact inverse. ▸ the exact inverse: invhilb(n) is the inverse of the n-square matrix with elements 1 i+j−1 . ▸ The result is exact for n less than about 15. Matrix Theory Matrices - 3/29

Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position(i,j)is l≤i,j≤n,is called a Hilbert matrix. Write down a Hilbert matrix for n=5. MATLAB command:hilb hb(n)is thenxn(nsquare)matrix with elements which is a famous example of a badly conditioned matrix.See INVHILB for the exact inverse. 命电有这女 Matrix Theory Matrices -3/29

Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position (i, j) is 1 i+j−1 , 1 ≤ i, j ≤ n, is called a Hilbert matrix. Write down a Hilbert matrix for n = 5. MATLAB command: hilb ▸ hilb(n) is the n × n (n-square) matrix with elements 1 i+j−1 , which is a famous example of a badly conditioned matrix. See INVHILB for the exact inverse. ▸ the exact inverse: invhilb(n) is the inverse of the n-square matrix with elements 1 i+j−1 . ▸ The result is exact for n less than about 15. Matrix Theory Matrices - 3/29

Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position(i,j)is l≤i,j≤n,is called a Hilbert matrix. Write down a Hilbert matrix for n=5. MATLAB command:hilb hb(n)is thenxn(nsquare)matrix with elements which is a famous example of a badly conditioned matrix.See INVHILB for the exact inverse. the exact inverse:invhilb(n)is the inverse of the n-square matrix with elements-1. 务老这头 Matrix Theory Matrices -3/29

Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position (i, j) is 1 i+j−1 , 1 ≤ i, j ≤ n, is called a Hilbert matrix. Write down a Hilbert matrix for n = 5. MATLAB command: hilb ▸ hilb(n) is the n × n (n-square) matrix with elements 1 i+j−1 , which is a famous example of a badly conditioned matrix. See INVHILB for the exact inverse. ▸ the exact inverse: invhilb(n) is the inverse of the n-square matrix with elements 1 i+j−1 . ▸ The result is exact for n less than about 15. Matrix Theory Matrices - 3/29

Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position(i,j)is l≤i,j≤n,is called a Hilbert matrix. Write down a Hilbert matrix for n=5. MATLAB command:hilb hb(n)is thenxn(nsquare)matrix with elements which is a famous example of a badly conditioned matrix.See INVHILB for the exact inverse. the exact inverse:invhilb(n)is the inverse of the n-square matrix with elementsj. The result is exact for n less than about 15. Matrix Theory Matrices -3/29

Hilbert Matrix Hilbert Matrix A square matrix of order n whose element in position (i, j) is 1 i+j−1 , 1 ≤ i, j ≤ n, is called a Hilbert matrix. Write down a Hilbert matrix for n = 5. MATLAB command: hilb ▸ hilb(n) is the n × n (n-square) matrix with elements 1 i+j−1 , which is a famous example of a badly conditioned matrix. See INVHILB for the exact inverse. ▸ the exact inverse: invhilb(n) is the inverse of the n-square matrix with elements 1 i+j−1 . ▸ The result is exact for n less than about 15. Matrix Theory Matrices - 3/29

Circulant Matrix Outline Hilbert Matrix Circulant Matrix Toeplitz Matrix Hankel Matrix Vandermonde Matrix Summary Questions Extensive reading 色老有这女子 Matrix Theory Matrices -4/29

Circulant Matrix Outline Hilbert Matrix Circulant Matrix Toeplitz Matrix Hankel Matrix Vandermonde Matrix Summary & Questions Extensive reading Matrix Theory Matrices - 4/29

Circulant Matrix Circulant Matrix A circulant matrix is a square matrix generated from a vector as the first row (or column), successive rows use the same elements as the first row,but each such row is circularly shifted by one element. 命电有这女子 Matrix Theory Matrices -5/29

Circulant Matrix Circulant Matrix A circulant matrix is ▸ a square matrix generated from a vector as the first row (or column), ▸ successive rows use the same elements as the first row, but each such row is circularly shifted by one element. Matrix Theory Matrices - 5/29