电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第六章 Green函数法 6.2 Dirichlet问题求解（1/2）

§6.2 Dirichlet问题求解 Dirichlet问题（第一类边值问题） △u=f(x,y,z),(x,y,z)∈V luls =o(x,y,z) 定义满足以下定解问题的解称边界面为S的Dirichlet问题的Green函数 △G=-6(x-5,y-n,z-5),(x,y,z)∈V) Gs=0 因品 △G=-δ(M-Mo),(x,y,z)∈V) Dhiricblet前圆 Gs=0

§6.2 Dirichlet问题求解 2 Dirichlet问题（第一类边值问题） ( , , ), ( , , ) ( , , ) S u f x y z x y z V u x y z           , , ,(( , , ) )  S 0 G x y z x y z V G                 定义 满足以下定解问题的解称边界面为S的Dirichlet问题的Green函数  0 ,(( , , ) ) S 0 G M M x y z V G           

定理1 △w=-f(x,Jy,z),(x,y,z)∈V) us=o(x,y,z) 的解的积分表达式为 =-年o()2C+oM:,wM 证明： ∫aG=-(M-M),(M∈V) Gs=0 G=G(M;Mo) w-s-a-aw∯到含0s-aw-an u(M)=u(M)*(M)(M)(M-M)dM. 3

3 定理1 ( , , ),(( , , ) ) ( , , ) S u f x y z x y z V u x y z           的解的积分表达式为   0 0 0 0 0 ( ; ) ( ) ( ; ) ( ) S V G M M u M M dS G M M f M dM n         证明：  0 ,( ) S 0 G M M M V G            v u u v dS v u u v dV                u v v u dS v udV u vdV n n                      0 G G M M  ( ; ) ( ) ( ) ( )   0 0 0   V u M u M M u M M M dM       

到会）s-0ww-ar u(M)=Su(M)5(M-M.)dM.=-Su(M,)AG(M:M,)dM, As-fd. G(MM)M,es=0,4s=pM） 4M=-∯()2co2s+∬a(wM/Mw

4 ( ) ( )0 0 0   V u M u M M M dM     0 0 0 ( ) ( ; ) V     u M G M M dM   0 0 0 0 0 ( ; ) ( ) ( ; ) ( ) S V G M M u M M dS G M M f M dM n         0 0 0 G M M u M ( ; ) 0, ( ) M S S     0 0 0 0 0 ( ; ) ( ; ) ( ) ( ; ) S V u G M M G M M u M dS G M M udM n n                 u v v u dS v udV u vdV n n                     

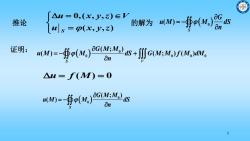
△u=0,(x,y,z)∈Y 推论 luls=o(x,y,z) 的解为)=-乎o()8%w 证明： an=-∯p()2GMs+aa1W. △u=f(M)=0 w=-∯p)Cs 5

5    u f M( ) 0   0 0 ( ; ) ( ) S G M M u M M dS n       0,( , , ) ( , , ) S u x y z V u x y z          推论 的解为 ( )  0  S G u M M dS n       证明：   0 0 0 0 0 ( ; ) ( ) ( ; ) ( ) S V G M M u M M dS G M M f M dM n        