电子科技大学：《矩阵理论 Matrix Theory》课程教学资源（课件讲稿）09 Vector norm

Matrix Theory -Vector Norms School of Mathematical Sciences Teaching Group Textbook: llse C.F.Ipsen,Numerical Matrix Analysis:Linear Systems and Least Squares.SIAM, 2009. Reference books: Fuzhen Zhang.Matrix Theory-Basic Results and Techniques,Second Edition. Springer,2011. Roger A.Horn and Charles A.Johnson:Matrix Analysis.Cambridge University Press,1985. Gene H.Golub and Charles F.Van Loan:Matrix Computations,Third Edition. Johns Hopkins Press,1996. Nicholas J.Higham.Accuracy and Stability of Numerical Algorithms,Second Edition.SIAM,2002. Y.Saad.Iterative Methods for Sparse Linear Systems,Second Edition.SIAM, Philadelphia,2003. Matrix Theory Vector Norms Maintained by Yan-Fei Jing

Textbook: Ilse C. F. Ipsen, Numerical Matrix Analysis: Linear Systems and Least Squares. SIAM, 2009. Reference books: ▸ Fuzhen Zhang. Matrix Theory-Basic Results and Techniques, Second Edition. Springer, 2011. ▸ Roger A. Horn and Charles A. Johnson: Matrix Analysis. Cambridge University Press, 1985. ▸ Gene H. Golub and Charles F. Van Loan: Matrix Computations, Third Edition. Johns Hopkins Press, 1996. ▸ Nicholas J. Higham. Accuracy and Stability of Numerical Algorithms, Second Edition. SIAM, 2002. ▸ Y. Saad. Iterative Methods for Sparse Linear Systems, Second Edition. SIAM, Philadelphia, 2003. Maintained by Yan-Fei Jing Matrix Theory ––Vector Norms School of Mathematical Sciences Teaching Group Matrix Theory Vector Norms

Introduction Outline Introduction Definition Two Important Inequalities Exercises Normwise Errors Comprehensive Problems Hold Inequality again 参老年这头 Matrix Theory Vector Norms -2/39

Introduction Outline Introduction Definition Two Important Inequalities Exercises Normwise Errors Comprehensive Problems H¨old Inequality again Matrix Theory Vector Norms - 2/39

Introduction Introduction In the context of linear system solution,the error in the solution constitutes a vector. r=b-A×X. 奇电有这头 Matrix Theory Vector Norms -3/39

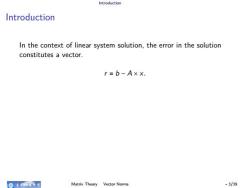
Introduction Introduction In the context of linear system solution, the error in the solution constitutes a vector. r = b − A × x. ▸ If we do not want to pay attention to individual components of the error, perhaps because there are too many components, then we can combine all errors into a single number. ▸ This is akin to a grade point average which combines all grades into a single number. ▸ Mathematically, this “combining” is accomplished by norms. Matrix Theory Vector Norms - 3/39

Introduction Introduction In the context of linear system solution,the error in the solution constitutes a vector. r=b-A×X. If we do not want to pay attention to individual components of the error,perhaps because there are too many components, then we can combine all errors into a single number. 奇电有这头 Matrix Theory Vector Norms -3/39

Introduction Introduction In the context of linear system solution, the error in the solution constitutes a vector. r = b − A × x. ▸ If we do not want to pay attention to individual components of the error, perhaps because there are too many components, then we can combine all errors into a single number. ▸ This is akin to a grade point average which combines all grades into a single number. ▸ Mathematically, this “combining” is accomplished by norms. Matrix Theory Vector Norms - 3/39

Introduction Introduction In the context of linear system solution,the error in the solution constitutes a vector. r=b-A×X. If we do not want to pay attention to individual components of the error,perhaps because there are too many components, then we can combine all errors into a single number. This is akin to a grade point average which combines all grades into a single number. 命电有这女 Matrix Theory Vector Norms -3/39

Introduction Introduction In the context of linear system solution, the error in the solution constitutes a vector. r = b − A × x. ▸ If we do not want to pay attention to individual components of the error, perhaps because there are too many components, then we can combine all errors into a single number. ▸ This is akin to a grade point average which combines all grades into a single number. ▸ Mathematically, this “combining” is accomplished by norms. Matrix Theory Vector Norms - 3/39

Introduction Introduction In the context of linear system solution,the error in the solution constitutes a vector. r=b-A×X. If we do not want to pay attention to individual components of the error,perhaps because there are too many components, then we can combine all errors into a single number. This is akin to a grade point average which combines all grades into a single number. Mathematically,this "combining"is accomplished by norms. 命电有这女子 Matrix Theory Vector Norms -3/39

Introduction Introduction In the context of linear system solution, the error in the solution constitutes a vector. r = b − A × x. ▸ If we do not want to pay attention to individual components of the error, perhaps because there are too many components, then we can combine all errors into a single number. ▸ This is akin to a grade point average which combines all grades into a single number. ▸ Mathematically, this “combining” is accomplished by norms. Matrix Theory Vector Norms - 3/39

Introduction Introduction In the context of linear system solution,the error in the solution constitutes a vector. r =b-A xx. If we do not want to pay attention to individual components of the error,perhaps because there are too many components, then we can combine all errors into a single number. This is akin to a grade point average which combines all grades into a single number. Mathematically,this "combining"is accomplished by norms. Start with vector norms,measuring the length of a vector. 色老有头习 Matrix Theory Vector Norms -3/39

Introduction Introduction In the context of linear system solution, the error in the solution constitutes a vector. r = b − A × x. ▸ If we do not want to pay attention to individual components of the error, perhaps because there are too many components, then we can combine all errors into a single number. ▸ This is akin to a grade point average which combines all grades into a single number. ▸ Mathematically, this “combining” is accomplished by norms. Start with vector norms, measuring the length of a vector. Matrix Theory Vector Norms - 3/39

Definition Outline Introduction Definition Two Important Inequalities Exercises Normwise Errors Comprehensive Problems Hold Inequality again 奇老有这女子 Matrix Theory Vector Norms -4/39

Definition Outline Introduction Definition Two Important Inequalities Exercises Normwise Errors Comprehensive Problems H¨old Inequality again Matrix Theory Vector Norms - 4/39

Definition Definition A vector norm is a function from Cn to R with three properties: 命电有这女子 Matrix Theory Vector Norms -5/39

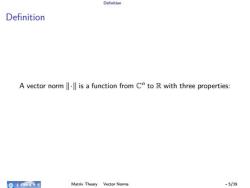
Definition Definition A vector norm ∣∣ ⋅ ∣∣ is a function from C n to R with three properties: Matrix Theory Vector Norms - 5/39

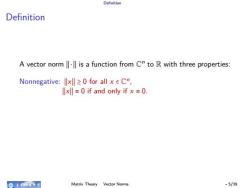
Definition Definition A vector norm is a function from Ch to R with three properties: Nonnegative:llxl≥0 for all x∈Cn, xI=0 if and only if x =0. 命电有这女子 Matrix Theory Vector Norms -5/39

Definition Definition A vector norm ∣∣ ⋅ ∣∣ is a function from C n to R with three properties: Nonnegative: ∣∣x∣∣ ≥ 0 for all x ∈ C n , ∣∣x∣∣ = 0 if and only if x = 0. Homogeneous: ∣∣αx∣∣ = ∣α∣∣∣x∣∣ for all α ∈ C, x ∈ C n . Triangle inequality: ∣∣x + y∣∣ ≤ ∣∣x∣∣ + ∣∣y∣∣ for all x, y ∈ C n . Matrix Theory Vector Norms - 5/39