《结晶学》课程教学资源（教案讲义）第五章 晶体定向与结晶符号

第五章晶体定向和结晶符号只要在生长时有足够的自由空间，晶体必然会长成由许多晶面和晶棱包围的几何多面体。在晶体上，所有的晶面、晶棱和角顶，它们的分布都是对称的。但除此而外，晶面和晶棱之间还有另一方面的几何关系，表现在晶面和晶棱相截或平行时，都可以用确定的数学形式来表征彼此间的空间取向关系。为了表达这种关系，首先需要在晶体中建立起一个坐标系，这就是晶体定向。所谓晶体定向，就是要在晶体上选择合理的三维坐标系，包括在晶体上选择坐标轴和确定各坐标轴的度量单位两项工作。在此基础上，就可以进一步确定晶面符号和晶棱符号，用数学的方式来表示各个晶面或晶棱在晶体上的方向，并反映出它们彼此间的几何关系。其中，平行于同一晶棱的若干晶面，特别称之为一个晶带。而整数定律则是进行上述这些工作的依据。在本章中，首先讨论晶体定向的原则，以便在晶体中建立起一个三维坐标系，在此基础上，分别叙述晶面符号和晶棱符号的构成。最后，再讲述整数定律以及有关晶带的问题。第一节结晶轴和晶体几何常数一、结晶轴的概念和选择原则1.结晶轴的概念晶体中的坐标轴称结晶轴，简称晶轴。晶轴是儿根假想的直线，沿着与晶体对称有关的限定方向穿过理想晶体，相交在晶体中心。2.晶轴的选择原则晶轴的选择不是任意的。首先，晶轴的选择要符合晶体自身的对称性，因此，要优先选择对称轴和对称面的法线方向。若晶体无对称轴和对称面或其数目不够时，则选合适的晶棱方向，在选择晶棱做晶轴时，可以设想将其平移至晶体中心。其次，在满足上述条件的前提下，应使晶轴尽可能互相垂直或近于垂直，并使轴单位尽可能相等，即使a=b=cα=β==90°。3.晶轴的安置及名称三轴定向：除三方晶系、六方晶系以外的晶体，均采用X、Y、Z三轴定向。X、55

55 第五章 晶体定向和结晶符号 只要在生长时有足够的自由空间，晶体必然会长成由许多晶面和晶棱包围的几 何多面体。在晶体上，所有的晶面、晶棱和角顶，它们的分布都是对称的。但除此 而外，晶面和晶棱之间还有另一方面的几何关系，表现在晶面和晶棱相截或平行时， 都可以用确定的数学形式来表征彼此间的空间取向关系。 为了表达这种关系，首先需要在晶体中建立起一个坐标系，这就是晶体定向。 所谓晶体定向，就是要在晶体上选择合理的三维坐标系，包括在晶体上选择坐标轴 和确定各坐标轴的度量单位两项工作。 在此基础上，就可以进一步确定晶面符号和晶棱符号，用数学的方式来表示各 个晶面或晶棱在晶体上的方向，并反映出它们彼此间的几何关系。其中，平行于同 一晶棱的若干晶面，特别称之为一个晶带。而整数定律则是进行上述这些工作的依 据。 在本章中，首先讨论晶体定向的原则，以便在晶体中建立起一个三维坐标系， 在此基础上，分别叙述晶面符号和晶棱符号的构成。最后，再讲述整数定律以及有 关晶带的问题。 第一节 结晶轴和晶体几何常数 一、结晶轴的概念和选择原则 ⒈ 结晶轴的概念 晶体中的坐标轴称结晶轴，简称晶轴。晶轴是几根假想的直线，沿着与晶体对 称有关的限定方向穿过理想晶体，相交在晶体中心。 ⒉ 晶轴的选择原则 晶轴的选择不是任意的。首先，晶轴的选择要符合晶体自身的对称性，因此， 要优先选择对称轴和对称面的法线方向。若晶体无对称轴和对称面或其数目不够时， 则选合适的晶棱方向，在选择晶棱做晶轴时，可以设想将其平移至晶体中心。 其次，在满足上述条件的前提下，应使晶轴尽可能互相垂直或近于垂直，并使 轴单位尽可能相等，即使 a=b=c α=β=γ=90°。 ⒊ 晶轴的安置及名称 三轴定向：除三方晶系、六方晶系以外的晶体，均采用 X、Y、Z 三轴定向。X

Y、Z晶轴的安置是：Z轴直立，上端为正：X轴前后，前端为正：Y轴左右，右端为正。轴角：X、Y、Z晶轴正端之间的夹角为轴角。分别用α（YΛZ)、β（ZΛX)、（YΛZ）表示，如图5-1。四轴定向：三方、六方晶系的晶体采用X、Y、U、Z四轴定向。四根轴的安置是：其中Z轴为直立轴，上端为正。X、Y、U为三个水平轴，Y轴左右，右端为正；X轴为左前，前端为正：U轴右前，后端为正。水平晶轴X、Y、U正端之间的夹角为120°（图5-2、5-3）。Z(+)Z(+)U(+)(-)U(+)BPIY(+)Y(+)Y(+)1X(+)X(+)X(+)图5-1三轴定向晶轴的安置和轴角图5-2四轴定向晶轴的安置图5-3四轴定向水平晶轴的安置二、轴单位（轴长）和轴率1.轴单位：晶轴的度量单位称轴单位，轴单位是与相应晶轴平行的行列上的结点间距，X、Y、Z轴上的结点间距用a、b、c表示。结点间距很小，需借助X射线衍射测定。目前，绝大多数的晶体结构都已测定，轴单位和轴角是已知的，对于晶体的外形来说，重要的不是三个轴单位的具体长度，而是它们的比率。2.轴率：将轴单位进行连比，记为a:b:c，称为轴率。轴率通常以b的长度作为单位长度，写成以b为1的连比式，例如橄榄石的轴率是0.46575:1:0.58651。三、晶体几何常数轴率a:b:c和轴角α、β、合称晶体几何常数，这是表示晶体坐标系统特征的一组参数，与晶体内部结构研究中的晶胞参数相同。不同晶系的晶体，具有不同规律的晶体常数；同一晶系的不同晶体，晶体常数的规律相同，但具体数值不等。知道晶体几何常数以后，就可以知道晶体构造中晶胞的形状，如果再用X射线晶体结构分析测得轴单位的具体长度，就可以知道晶胞的大小。例如橄榄石，晶体常数为a:b:c=0.46575:1:0.58651，α=β==90°，晶胞形状像火柴盒。闪锌矿，a:b:c=1:1:1α=β==90°，晶胞形状为立方体，若测得a=0.540nm，可知晶胞是棱长为0.540nm的立方体。56

56 Y、Z 晶轴的安置是：Z 轴直立，上端为正；X 轴前后，前端为正；Y 轴左右，右端 为正。 轴角：X、Y、Z 晶轴正端之间的夹角为轴角。分别用 α（Y∧Z）、β（Z∧X）、γ （Y∧Z）表示，如图 5-1。 四轴定向：三方、六方晶系的晶体采用 X、Y、U、Z 四轴定向。四根轴的安置 是：其中 Z 轴为直立轴，上端为正。X、Y、U 为三个水平轴，Y 轴左右，右端为正； X 轴为左前，前端为正；U 轴右前，后端为正。水平晶轴 X、Y、U 正端之间的夹角 为 120°（图 5-2、5-3）。 图 5-1 三轴定向晶轴的安置和轴角 图 5-2 四轴定向晶轴的安置 图 5-3 四轴定向水平晶轴的安置 二、轴单位（轴长）和轴率 ⒈ 轴单位：晶轴的度量单位称轴单位，轴单位是与相应晶轴平行的行列上的结 点间距，X、Y、Z 轴上的结点间距用 a、b、c 表示。结点间距很小，需借助 X 射线 衍射测定。目前，绝大多数的晶体结构都已测定，轴单位和轴角是已知的，对于晶 体的外形来说，重要的不是三个轴单位的具体长度，而是它们的比率。 ⒉ 轴率：将轴单位进行连比，记为 a:b:c，称为轴率。轴率通常以 b 的长度作为 单位长度，写成以 b 为 1 的连比式，例如橄榄石的轴率是 0.46575:1:0.58651。 三、晶体几何常数 轴率 a:b:c 和轴角 α、β、γ 合称晶体几何常数，这是表示晶体坐标系统特征的一 组参数，与晶体内部结构研究中的晶胞参数相同。 不同晶系的晶体，具有不同规律的晶体常数；同一晶系的不同晶体，晶体常数 的规律相同，但具体数值不等。 知道晶体几何常数以后，就可以知道晶体构造中晶胞的形状，如果再用 X 射线 晶体结构分析测得轴单位的具体长度，就可以知道晶胞的大小。 例如橄榄石，晶体常数为 a:b:c=0.46575:1:0.58651，α=β=γ=90°，晶胞形状像火 柴盒。闪锌矿，a:b:c=1:1:1,α=β=γ=90°，晶胞形状为立方体，若测得 a=0.540nm，可 知晶胞是棱长为 0.540nm 的立方体

第二节各晶系晶轴的选择及其晶体常数特点不同晶系的对称特点是各不相同的。为了更好地适应于晶体的对称性，在选择结晶轴的总原则不变的前提下，对于不同晶系的晶体，选择结晶轴的具体法则也应有所不同。相应地，它们的晶体几何常数特征也将表现出一定的差异。由于三方晶系和六方晶系对称的特殊性，因而它们的晶体定向也与其他晶系有较大的不同，采用四轴定向：除了三方晶系和六方晶系之外，其它几个晶系采用三轴定向，即选择三个结晶轴的晶体定向。现将各晶系晶体的具体定向法则，分别叙述如下：1.等轴晶系（1）对称特点：必有三个互相垂直的L或L，或L，理想发育的晶体总沿这三个方向呈等长状态，这三个方向可以借助于L的作用互相重复，因此晶体在这三个方向的性质相同，结点间距相等。(2）选轴原则：以互相垂直的3L*或3L为X、Y、Z轴；没有四次轴时选择互相垂直的3L-为X、Y、Z轴。并使Z轴直立，Y轴左右，X轴前后。见图5-4。(3）晶体几何常数：a=b=c，α=β==90°。轴率a:b:c=1:1:1。1X11ba图5-4等轴晶系品轴的选择与安置a=b=c，=β-=90°（a-闪锌矿：b-方铅矿）2.四方晶系(1）对称特点：必有而且只有一个L或L4，晶体沿四次轴发育较长或较短。(2）选轴原则：以L*或L为Z轴，以与L或L垂直且互相垂直的两个L为X、Y轴，两者分别位于前后、左右方向；如果晶体无L时，则选择两个互相垂直的对称面法线方向为X、Y轴；如既无L?也无对称面时，则选择合适的晶棱方向为X、57

57 第二节 各晶系晶轴的选择及其晶体常数特点 不同晶系的对称特点是各不相同的。为了更好地适应于晶体的对称性，在选择 结晶轴的总原则不变的前提下，对于不同晶系的晶体，选择结晶轴的具体法则也应 有所不同。相应地，它们的晶体几何常数特征也将表现出一定的差异。 由于三方晶系和六方晶系对称的特殊性，因而它们的晶体定向也与其他晶系有 较大的不同，采用四轴定向；除了三方晶系和六方晶系之外，其它几个晶系采用三 轴定向，即选择三个结晶轴的晶体定向。 现将各晶系晶体的具体定向法则，分别叙述如下 ： ⒈ 等轴晶系 ⑴ 对称特点：必有三个互相垂直的 L 4 或 Li 4 或 L 2，理想发育的晶体总沿这三个 方向呈等长状态，这三个方向可以借助于 L 3 的作用互相重复，因此晶体在这三个方 向的性质相同，结点间距相等。 ⑵ 选轴原则：以互相垂直的 3L4 或 3Li 4 为 X、Y、Z 轴；没有四次轴时选择互 相垂直的 3L2 为 X、Y、Z 轴。并使 Z 轴直立，Y 轴左右，X 轴前后。见图 5-4。 ⑶ 晶体几何常数：a =b=c， α=β=γ=90°。轴率 a:b:c =1:1:1。 a b 图 5-4 等轴晶系晶轴的选择与安置 a=b=c，α=β=γ=90o（a-闪锌矿；b-方铅矿） ⒉ 四方晶系 ⑴ 对称特点：必有而且只有一个 L 4 或 Li 4，晶体沿四次轴发育较长或较短。 ⑵ 选轴原则：以 L 4 或 Li 4 为 Z 轴，以与 L 4 或 Li 4 垂直且互相垂直的两个 L 2 为 X、 Y 轴，两者分别位于前后、左右方向；如果晶体无 L 2 时，则选择两个互相垂直的对 称面法线方向为 X、Y 轴；如既无 L 2 也无对称面时，则选择合适的晶棱方向为 X

Y轴。见图5-5。(3）晶体几何常数：a=btc，α=β==90°。轴率a:c（因a=b，故轴率以a:c表示）的值因晶体种类不同而不同，例如锆石a:c=1:0.64037，黄铜矿a:c=1:1.97050。3.斜方晶系(1）对称特点：L2和P的总数不少于三个，且3L2或L2与2P法线互相垂直。(2）选轴原则：有3L2时，以此互相垂直的3L2为X、Y、Z轴：在L?2P中，以L?为Z轴，2P法线为X、Y轴。见图5-6。(3）晶体几何常数：a+b+c，α=β==90°，轴率a:b:c因晶体种类不同而不同，如文石a:b:c=0.62244:1:0.72056。ZZ010X/TO图5-6斜方晶系晶轴的选择与安置图5-5四方晶系晶轴的选择与安置a=b+c,=β==90°ab+c,a=β==90°（锆石a:c=1:0.6404）（十字石a:b:c=0.47341:0.6828）4.单斜晶系(1）对称特点：L或P的个数不多于1个，在L"PC中，L2与P的法线重合。(2）选轴原则：以L或P的法线为Y轴，以两根均垂直Y轴的合适晶棱方向为X、Z轴。X、Z轴均与Y轴垂直，X轴与Z轴不垂直。安置晶轴时，使Z轴直立，Y轴左右水平，X轴前后并向前下方倾斜（图5-7）。(3）晶体几何常数：ab+c，α==90°，β>90°，轴率a:b:c的具体数值在不同种的晶体中不同。5.三斜晶系：(1）对称特点：只有L和C。(2）选轴原则：以三根合适显著的晶棱方向为X、Y、Z轴。晶轴安置：先使Z轴直立，然后使Y轴左右并向右下倾斜。此时，X轴应居于前后并向前下倾斜（图5-8)。(3）晶体几何常数：abtc，α邦+90°。轴率a:b:c值和轴角α、β、值均因晶体种类不同而异。58

58 Y 轴。见图 5-5。 ⑶ 晶体几何常数：a=b≠c，α=β=γ=90°。轴率 a:c（因 a = b， 故轴率以 a:c 表 示）的值因晶体种类不同而不同，例如锆石 a:c=1:0.64037，黄铜矿 a:c=1:1.97050。 ⒊ 斜方晶系 ⑴ 对称特点：L 2 和 P 的总数不少于三个，且 3L2 或 L 2 与 2P 法线互相垂直。 ⑵ 选轴原则：有 3L2 时，以此互相垂直的 3L2 为 X、Y、Z 轴；在 L 2 2P 中，以 L 2 为 Z 轴，2P 法线为 X、Y 轴。见图 5-6。 ⑶ 晶体几何常数：a≠b≠c，α=β=γ=90°，轴率 a:b:c 因晶体种类不同而不同，如 文石 a:b:c=0.62244:1:0.72056。 图 5-5 四方晶系晶轴的选择与安置 图 5-6 斜方晶系晶轴的选择与安置 a＝b≠c,α=β=γ=90o a≠b≠c,α=β=γ=90o （锆石 a:c=1:0.6404） （十字石 a:b:c=0.47341:0.6828） ⒋ 单斜晶系 ⑴ 对称特点：L 2 或 P 的个数不多于 1 个，在 L 2 PC 中，L 2 与 P 的法线重合。 ⑵ 选轴原则：以 L 2 或 P 的法线为 Y 轴，以两根均垂直 Y 轴的合适晶棱方向为 X、Z 轴。X、Z 轴均与 Y 轴垂直，X 轴与 Z 轴不垂直。安置晶轴时，使 Z 轴直立， Y 轴左右水平，X 轴前后并向前下方倾斜（图 5-7）。 ⑶ 晶体几何常数：a≠b≠c，α=γ=90°，β>90°，轴率 a:b:c 的具体数值在不同种 的晶体中不同。 ⒌三斜晶系： ⑴ 对称特点：只有 L 1 和 C。 ⑵ 选轴原则：以三根合适显著的晶棱方向为 X、Y、Z 轴。晶轴安置：先使 Z 轴直立，然后使 Y 轴左右并向右下倾斜。此时，X 轴应居于前后并向前下倾斜（图 5-8）。 ⑶ 晶体几何常数：a≠b≠c，α≠β≠γ≠90° 。轴率 a:b:c 值和轴角 α、β、γ 值均因 晶体种类不同而异。 001 110 010 110 101 101 Z Y X

图5-7单斜晶系晶轴的选择与安置图5-8三斜晶系晶轴的选择与安置abc,==90°β>90°a+b+c,a++90°（石a:b:c=0.7547:1:0.8543,β=119.430)(钠长石a:b:c=0.6335:1:0.5577,β=94.3°)6.三方及六方晶系（四轴定向）（1）对称特点：有且只有一个L或L（L‘），晶体往往沿此方向发育较长或较短。(2）选轴原则：以唯一的高次轴为Z轴，以与Z垂直且彼此成60°角相交的3L2或3P法线或三条适当晶棱方向为X、Y、U轴。(3）晶体几何常数：a=b+c，α=β=90°，=120°。轴率a:c具体数值不同。Z00010T1ITT图5-9三方及六方晶系晶轴的选择与安置a=b+c,α=β=90°，=120°左：方解石a:c=:1:0.8543，右：绿柱石a:c=1:0.4989，综上所述，在晶体的三轴定向中，选择结晶轴的一般步骤是：有四次轴时优先选择四次轴，四次轴不够或没有时选择L，L不够或没有时选择P的法线，最后连P的法线也不够或没有时，选择合适的晶棱方向。在以上的选择中，除单斜晶系优先考虑Y轴之外，其余皆优先考虑Z轴。最后，还有两种情况需要加以说明。按照上述的晶体定向的具体法则，结晶轴选择的可能性往往并不是唯一的。一种情况是，例如对一个四方柱状晶体（四方晶59

59 图 5-7 单斜晶系晶轴的选择与安置 图 5-8 三斜晶系晶轴的选择与安置 a≠b≠c,α =γ=90o ，β＞90o a≠b≠c,α≠β≠γ≠90o （榍石 a:b:c=0.7547:1:0.8543, β=119.43O） （钠长石 a:b:c=0.6335:1:0.5577, β=94.3o） ⒍ 三方及六方晶系（四轴定向） ⑴ 对称特点：有且只有一个 L 3 或 L 6（Li 6），晶体往往沿此方向发育较长或较短。 ⑵ 选轴原则：以唯一的高次轴为 Z 轴，以与 Z 垂直且彼此成 60°角相交的 3L2 或 3P 法线或三条适当晶棱方向为 X、Y、U 轴。 ⑶ 晶体几何常数：a=b≠c，α=β=90°，γ=120°。轴率 a:c 具体数值不同。 图 5-9 三方及六方晶系晶轴的选择与安置 a＝b≠c,α=β=90o ，γ=120o 左：方解石 a:c=:1:0.8543, 右：绿柱石 a:c=1:0.4989, 综上所述，在晶体的三轴定向中，选择结晶轴的一般步骤是：有四次轴时优先 选择四次轴，四次轴不够或没有时选择 L 2，L 2 不够或没有时选择 P 的法线，最后连 P 的法线也不够或没有时，选择合适的晶棱方向。 在以上的选择中，除单斜晶系优先考虑 Y 轴之外，其余皆优先考虑 Z 轴。 最后，还有两种情况需要加以说明。按照上述的晶体定向的具体法则，结晶轴 选择的可能性往往并不是唯一的。一种情况是，例如对一个四方柱状晶体（四方晶

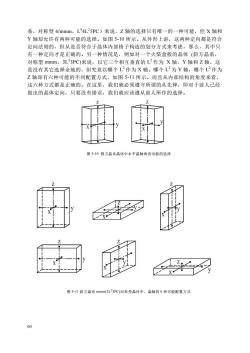
系，对称型4/mmm，L*4L25PC）来说，Z轴的选择只有唯一的一种可能，但X轴和Y轴却允许有两种可能的选择。如图5-10所示。从外形上讲，这两种定向都是符合定向法则的，但从是否符合于晶体内部格子构造的划分方式来考虑，那么，其中只有一种定向才是正确的。另一种情况是，例如对一个火柴盒般的晶体（斜方晶系，对称型mmm，3L?3PC)来说，以它三个相互垂直的L2作为X轴、Y轴和Z轴，这是没有其它选择余地的，但究竞以哪个L?作为X轴。哪个L为Y轴，哪个L作为Z轴却有六种可能的不同配置方式，如图5-11所示。而且从内部结构的角度来看，这六种方式都是正确的。在这里，我们就必须遵守所谓的从先律，即对于前人已经做出的晶体定向，只要没有错误，我们就应该遵从前人所作的选择。Z图5-10四方晶系晶体中水平晶轴两套可能的选择Z图5-11斜方晶系mmm（3L-3PC）对称型晶体中，晶轴的6种可能配置方式60

60 系，对称型 4/mmm，L 4 4L2 5PC）来说，Z 轴的选择只有唯一的一种可能，但 X 轴和 Y 轴却允许有两种可能的选择。如图 5-10 所示。从外形上讲，这两种定向都是符合 定向法则的，但从是否符合于晶体内部格子构造的划分方式来考虑，那么，其中只 有一种定向才是正确的。另一种情况是，例如对一个火柴盒般的晶体 (斜方晶系， 对称型 mmm，3L2 3PC)来说，以它三个相互垂直的 L 2 作为 X 轴、Y 轴和 Z 轴，这 是没有其它选择余地的，但究竟以哪个 L 2 作为 X 轴。哪个 L 2 为 Y 轴，哪个 L 2 作为 Z 轴却有六种可能的不同配置方式，如图 5-11 所示。而且从内部结构的角度来看， 这六种方式都是正确的。在这里，我们就必须遵守所谓的从先律，即对于前人已经 做出的晶体定向，只要没有错误，我们就应该遵从前人所作的选择。 图 5-10 四方晶系晶体中水平晶轴两套可能的选择 图 5-11 斜方晶系 mmm(3L2 3PC)对称型晶体中，晶轴的 6 种可能配置方式

各晶系晶轴的选择及晶体几何常数特点见表5-1。表5-1各晶系选择晶轴的原则及晶体几何常数晶体晶系选择晶轴的原则几何常数以相互垂直的3L或3L4为晶轴，无L*或L"时，以相互垂a=b=c等轴晶系直的3L2为晶轴α=β==90°以L4或L4为Z轴，以与L或L垂直且互相垂直的两个a=b+c四方晶系L?或2P法线方向为X、Y轴，如无L?和P，则选择合适的晶棱Q=β==90°方向为X、Y轴。a=b+c三方及以唯一的高次轴为Z轴，以与Z垂直且彼此成60°相交的α=β=90°六方晶系3L或3P法线或三条适当晶棱方向为X、Y、U轴。=120°有3L时，以3L为X、Y、Z轴：在L2P中，以L为Zatb+c斜方晶系轴，2P法线为X、Y轴。α=β==90°atb+c以L?或P法线为Y轴，以两根均垂直Y轴的合适晶棱方向单斜晶系α==90°,为X、Z轴，β>90°atbc三斜晶系以三根合适显著的晶棱方向为X、Y、Z轴++90°第三节晶面符号在完成了晶体的定向工作，也就是在晶体上建立了三维坐标系之后，就可以用简单的数字符号，表示晶面在晶体上的位置，这种数字符号称为晶面符号。晶面符号有不同类型，通常采用的是米氏符号，是英国人米勒尔(W.H.Miller)在1839年提出的。一、米氏符号的构成与晶面指数的确定米氏符号：用晶面在各晶轴上截距系数的倒数比表示晶面在晶体上位置的简单数字符号。1.米氏符号的构成（图5-12）：假设有一任意晶面HKL，它在X、Y、Z轴上的截距为OH、OK、OL.X、Y、Z轴的轴单位为a、b、C，求晶面符号。已知晶面HKL在X、Y、Z轴上的截距分别为：OH=2a，OK=3b，OL=6c，晶面在X、Y、Z轴上的载距系数的倒数比为1/2：1/3：1/6，化整成为3：2：1，去比例号，加小括号，写成（321），即为该晶面的米氏符号。小括号内的数字称为晶面指数。三轴定向的晶面指数按X、Y、Z轴的顺序排列，61

61 各晶系晶轴的选择及晶体几何常数特点见表 5-1。 表 5-1 各晶系选择晶轴的原则及晶体几何常数 晶 系 选 择 晶 轴 的 原 则 晶 体 几何常数 等轴晶系 以相互垂直的 3L4 或 3Li 4 为晶轴，无 L 4 或 Li 4 时，以相互垂 直的 3L2 为晶轴 a=b=c α=β=γ=90° 四方晶系 以 L 4 或 Li 4 为 Z 轴，以与 L 4 或 Li 4 垂直且互相垂直的两个 L 2 或 2P 法线方向为 X、Y 轴，如无 L 2 和 P，则选择合适的晶棱 方向为 X、Y 轴。 a=b≠c α=β=γ=90° 三 方 及 六方晶系 以唯一的高次轴为 Z 轴，以与 Z 垂直且彼此成 60°相交的 3L2 或 3P 法线或三条适当晶棱方向为 X、Y、U 轴。 a=b≠c α=β=90° γ=120° 斜方晶系 有 3L2 时，以 3L2 为 X、Y、Z 轴；在 L 2 2P 中，以 L 2 为 Z 轴， 2P 法线为 X、Y 轴。 a≠b≠c α=β=γ=90° 单斜晶系 以 L 2 或 P 法线为 Y 轴，以两根均垂直 Y 轴的合适晶棱方向 为 X、Z 轴， a≠b≠c α=γ=90°， β>90o 三斜晶系 以三根合适显著的晶棱方向为 X、Y、Z 轴 a≠b≠c α≠β≠γ≠90° 第三节 晶面符号 在完成了晶体的定向工作，也就是在晶体上建立了三维坐标系之后，就可以用 简单的数字符号，表示晶面在晶体上的位置，这种数字符号称为晶面符号。 晶面符号有不同类型，通常采用的是米氏符号，是英国人米勒尔(W.H.Miller)在 1839 年提出的。 一、米氏符号的构成与晶面指数的确定 米氏符号：用晶面在各晶轴上截距系数的倒数比表示晶面在晶体上位置的简单 数字符号。 ⒈ 米氏符号的构成（图 5-12 ）：假设有一任意晶面 HKL，它在 X、Y、Z 轴上 的截距为 OH、OK、OL，X、Y、Z 轴的轴单位为 a、b、c，求晶面符号。 已知晶面 HKL 在 X、Y、Z 轴上的截距分别为：OH=2a，OK=3b，OL=6c，晶 面在 X、Y、Z 轴上的载距系数的倒数比为 1/2：1/3：1/6，化整成为 3：2：1，去比 例号，加小括号，写成（321），即为该晶面的米氏符号。 小括号内的数字称为晶面指数。三轴定向的晶面指数按 X、Y、Z 轴的顺序排列

不能颠倒，一般式写成（hkl)：四轴定向的晶面指数按X、Y、U、Z轴顺序排列，不能颠倒，一般式写成（hkil）。2.利用轴率确定晶面符号三轴定向的晶体，如果已知轴率a:b:c和晶面在各晶轴上的截距OH、OK、OL，晶面指数可直接由下式求出：h:k:/=a/OH:b/OK:c/OL四轴定向（三方、六方晶系）的晶体，由于有四个结晶轴，相应每个晶面就有四个晶面指数。此时，由于轴率总是1：1：1：c，故晶面指数可直接由下式求出：h:k:i:/=1/OH:1/OK:1/OI:C*/OLL图5-12求品面符号的图解图5-13证明h+k+i=0图解四轴定向中，晶面在水平晶轴上晶面指数的代数和为0。从数学角度来看，三个水平结晶轴中必定有一个是多余的。这就意味着，在对应于水平结晶轴的三个指数h、k、i中，必定只有两个是独立的参数：三者之间有某种确定的关系，由其中的任意两者必定能确定第三者。根据四轴定向时三个水平结晶轴的正端互成120°交角的关系，在此应当有：h+k+i=0亦即与三个水平结晶轴相对应的晶面指数，它们的代数和永远为0。图5-13所示为包含三个水平结晶轴的平面，AB为某一晶面ABE与此平面相交的迹线。晶面ABE分别截X轴、Y轴、U轴于A、B、C，显然，OA、OB、OC即为晶面在X轴、Y轴、U轴上的截距。现过B点作U轴的平行线BD，BD交X轴于D点。根据三根水平晶轴之间的夹角关系可知OBD为等边三角形，因此(1)OB=OD=BD同时，AOCSADB(2)AD/DB=OA/OC即：（OA+OB）/OB=OA/OC62

62 不能颠倒，一般式写成（hkl）；四轴定向的晶面指数按 X、Y、U、Z 轴顺序排列， 不能颠倒，一般式写成（hk i l）。 ⒉ 利用轴率确定晶面符号 三轴定向的晶体，如果已知轴率 a:b:c 和晶面在各晶轴上的截距 OH 、OK、OL， 晶面指数可直接由下式求出： h:k:l=a/OH:b/OK:c/OL 四轴定向（三方、六方晶系）的晶体，由于有四个结晶轴，相应每个晶面就有 四个晶面指数。此时，由于轴率总是 1：1：1：c′，故晶面指数可直接由下式求出： h:k:i:l=1/OH:1/OK:1/OI:C′/OL 图 5-12 求晶面符号的图解 图 5-13 证明 h+k+i=0 图解 四轴定向中，晶面在水平晶轴上晶面指数的代数和为 0。从数学角度来看，三个 水平结晶轴中必定有一个是多余的。这就意味着，在对应于水平结晶轴的三个指数 h、 k、i 中，必定只有两个是独立的参数；三者之间有某种确定的关系，由其中的任意 两者必定能确定第三者。根据四轴定向时三个水平结晶轴的正端互成 120°交角的关 系，在此应当有： h +k +i = 0 亦即与三个水平结晶轴相对应的晶面指数，它们的代数和永远为 0。 图5-13所示为包含三个水平结晶轴的平面， AB 为某一晶面 ABE 与此平面相交 的迹线。晶面 ABE 分别截 X 轴、Y 轴、U 轴于 A、B、C，显然，OA、OB、OC 即 为晶面在 X 轴、Y 轴、U 轴上的截距。现过 B 点作 U 轴的平行线 BD，BD 交 X 轴 于 D 点。 根据三根水平晶轴之间的夹角关系可知 OBD 为等边三角形，因此 OB=OD=BD ⑴ 同时， AOC∽ADB AD/DB=OA/OC ⑵ 即： （OA+OB）/OB=OA/OC

简化后得：(3)1/OA）+（1/OB）-（1/OC）=0(4)根据关系式h:k:i:/=1/OH:1/OK:1/OI:C/OL对应于三个水平晶轴的晶面指数应为：(5)h=n/OA，k=n/OB，i=n/OC式中n为在简化晶面指数时所可能存在的公因数。将式(5)代入式(3)即得：h+k+i=0利用这一关系，可以给确定晶面符号的工作带来不少方便。如果晶面平行于某个晶轴时，晶面在此晶轴上的截距和截距系数都等于无穷大，相应的晶面指数等于0。这就是为什么不直接用截距系数，而是要用它们的倒数来作为晶面指数的原因。此外，在同一单形中如果有两个晶面相互平行，那么，根据相似三角形的原理，它们在三个结晶轴上的截距必定全都对应相等，但因它们分别位于原点的相反两侧，因而截距值的正负号则恰好相反。因此，对于同一单形的所有晶面来说，凡是相互平行的一对晶面，它们的晶面指数的绝对值必定对应相等，而正负号则均相反，例如（321)与（321）（001)与001)等。例1：八面体的某晶面与X、Y、Z轴正端等长相截，求该晶面的晶面符号。已知等轴晶系a=b=c，a:b:c=1:1:1，八面体晶面在三晶轴上的截距相等，即OH=OK=OL，则：h:k:/=1/OH:1/OK:1/OL=1:1:1，故晶面符号为(111)。例2：六方柱某晶面与X、Y轴正端等长相截，与Z轴平行，写出晶面符号。h:k:i:/=1/OH:1/0K:1/O1:c*/cg=1/OH:1/OH:2/OH:0=1:1:2:0由于晶面截X、Y轴与正端，则必截U轴于负端，故其晶面符号为（1120)。例3：六方双锥某晶面与X、Y轴正端等长相截与Z轴正端相截，求其晶面符号。h:k:i:/=1/OH:1/OH:2/OH:c/OL=1:1:2:c/OL该晶面的晶面符号为(hh2hl)。下面我们来看一下等轴晶系的黄铁矿晶体的具体实例。图5-14所示黄铁矿的晶体共有26个晶面，按它们的形状可分为三组，6个矩形晶面（标有记号a者），12个近于梯形的晶面（标有记号e者）：8个等边三角形晶面（标有记号o者）。晶体属m3(3L*4L3PC)对称型；每一对矩形晶面的垂线方向均为L，即以此三个相互垂直的L-为结晶轴。由于是等轴晶系晶体，故轴率a:b:c=l:1:1。在6个矩形晶面中，晶面a与X轴相截而与Y轴及Z轴平行，截距系数之比为1:00:00，其，倒数比为1:0:0。因此，晶面a的晶面符号应为（100)。与晶面a平行的另一晶面a4，截X轴于负端而与Y轴、Z轴平行，所以晶面a4的符号为（100)。晶面a及与之平行的晶面as，均与X轴及Z轴平行而与Y轴相截，其中a2截于正端而as则截于负端，因此，它们的晶面符号分别为（010)与(0i0)。晶面a3及与之平行63

63 简化后得： 1/OA）+（1/OB）－（1/OC）=0 ⑶ 根据关系式 h:k:i:l=1/OH:1/OK:1/OI:C„ /OL ⑷ 对应于三个水平晶轴的晶面指数应为： h=n/OA，k=n/OB，i=n/OC ⑸ 式中 n 为在简化晶面指数时所可能存在的公因数。将式⑸代入式⑶即得： h+k+i=0 利用这一关系，可以给确定晶面符号的工作带来不少方便。 如果晶面平行于某个晶轴时，晶面在此晶轴上的截距和截距系数都等于无穷大， 相应的晶面指数等于 0。这就是为什么不直接用截距系数，而是要用它们的倒数来作 为晶面指数的原因。 此外，在同一单形中如果有两个晶面相互平行，那么，根据相似三角形的原理， 它们在三个结晶轴上的截距必定全都对应相等，但因它们分别位于原点的相反两侧， 因而截距值的正负号则恰好相反。因此，对于同一单形的所有晶面来说，凡是相互 平行的一对晶面，它们的晶面指数的绝对值必定对应相等，而正负号则均相反，例 如 (321)与( 3 2 1 ) (001)与(001)等。 例 1：八面体的某晶面与 X、Y、Z 轴正端等长相截，求该晶面的晶面符号。 已知等轴晶系 a=b=c， a:b:c=1:1:1，八面体晶面在三晶轴上的截距相等，即 OH=OK=OL，则： h:k:l=1/OH:1/OK:1/OL=1:1:1 ，故晶面符号为(111)。 例 2：六方柱某晶面与 X、Y 轴正端等长相截，与 Z 轴平行，写出晶面符号。 h:k:i:l =1/OH:1/0K:1/OI:c′/∞ =1/OH:1/OH:2/OH:0 =1:1:2:0 由于晶面截 X、Y 轴与正端，则必截 U 轴于负端，故其晶面符号为(11 2 0)。 例 3：六方双锥某晶面与 X、Y 轴正端等长相截与 Z 轴正端相截，求其晶面符号。 h:k:i:l =1/OH:1/OH:2/OH:c′/OL =1:1:2: c′/OL 该晶面的晶面符号为(hh 2h l)。 下面我们来看一下等轴晶系的黄铁矿晶体的具体实例。 图5-14所示黄铁矿的晶体共有26个晶面，按它们的形状可分为三组，6个矩形晶 面(标有记号 a 者)，12个近于梯形的晶面(标有记号 e 者)；8个等边三角形晶面(标有 记号 o 者)。晶体属 m3(3L2 4L3 3PC)对称型；每一对矩形晶面的垂线方向均为 L 2，即 以此三个相互垂直的 L 2为结晶轴。由于是等轴晶系晶体，故轴率 a:b:c=l:1:1。 在6个矩形晶面中，晶面 a1与 X 轴相截而与 Y 轴及 Z 轴平行，截距系数之比为 1:∞:∞，其，倒数比为1:0:0。因此，晶面 a1的晶面符号应为(100)。与晶面 a1平行的 另一晶面 a4，截 X 轴于负端而与 Y 轴、Z 轴平行，所以晶面 a4的符号为( 1 00)。晶 面 a2及与之平行的晶面 a5，均与 X 轴及 Z 轴平行而与 Y 轴相截，其中 a2截于正端 而 a5则截于负端，因此，它们的晶面符号分别为(010)与(0 1 0)。晶面 a3及与之平行

的晶面a6则均与X轴、Y轴平行而与Z轴相截，相应的晶面符号应为(001)与(00i)。在12个近于梯形的晶面中，晶面ei延展后将与X轴及Y轴相截而与Z轴平行，ZLa图5-14黄铁矿品体定向及求品面符号图示图5-15正长石晶体的定向及求晶面符号图示它在三个晶轴上的截距系数之比为1:2:00，其倒数比为1/1:1/2:1/00=2:1:0，故e之晶面符号为（210)。晶面e2与e1不同之处仅在于它截Y轴于负端，故e2之晶面符号应为(2iO)。晶面e4与X轴平行而与Y轴及Z轴相截，截距系数之比为o0:1.2，相应的晶面符号为(021)：而晶面e6之符号则为（02i)。晶面es与Y轴平行而与X轴Z轴相截，截距系数之比为2:00:1，晶面符号为（102)：而晶面e3之符号则为（102）。除了这六个晶面外，近于梯形的晶面一共还有六个，它们分别位于晶体的后面和左面，同理得出它们的晶面符号。这样，12个近于梯形的晶面的晶面符号如下：(210)、（2i0）、（021）、（02i)、（102)、（102)(20)、（10）、（0）、(021)、(i02)、（i02)在8个三角形晶面中，晶面0延展后将与三个结晶轴均相交，且三个截距系数值也都相等，即为1:1:1，故其晶面符号为(111)。另外七个晶面的情况与01类似，只是与不同结晶轴截于正端或负端上有所差异。它们的晶面符号如下：)(i)(ii)、(i)(ii)、(il)(i)、(1i)以上上下对着写的两个晶面符号，代表晶体上相互平行的一对晶面。再例如单斜晶系的正长石晶体（图5-15)。其对称型为2/m(L’PC)，我们以L方向作为结晶轴Y轴，以m、a、b等晶面的交棱方向为Z轴，而以c、n、b等晶面的交棱方向为X轴；正长石晶体结构中相应方向上行列的重复周期，亦即晶胞的三根棱长为a=0.860nm，b=1.306nm，c=0.719nm，轴率a:b:c=0.6585:1:0.5554。此时晶面在三个结晶轴上的截距（指截距，不是指截距系数之比为2.270:1.148:00，则：h.k:1=0.6585/2.270:1/1.148:0.5554/co=0.2904:0.8712:0=1:3:0故正长石上晶面a之晶面符号为（130）。其他各晶面都可利用相同的关系式，根据各自的截距比，求出相应的晶面符号。64

64 的晶面 a6则均与 X 轴、Y 轴平行而与 Z 轴相截，相应的晶面符号应为(001)与(00 1 )。 在12个近于梯形的晶面中，晶面 el 延展后将与 X 轴及 Y 轴相截而与 Z 轴平行， 图5-14 黄铁矿晶体定向及求晶面符号图示 图5-15 正长石晶体的定向及求晶面符号图示 它在三个晶轴上的截距系数之比为1:2:∞，其倒数比为1/1:1/2:1/∞=2:1:0，故 el 之晶面 符号为 (210)。晶面 e2与 e1不同之处仅在于它截 Y 轴于负端，故 e2之晶面符号应为 (2 1 0)。晶面 e4与 X 轴平行而与 Y 轴及 Z 轴相截，截距系数之比为∞:1:2，相应的晶 面符号为(021)；而晶面 e6之符号则为(02 1 )。晶面 e5与 Y 轴平行而与 X 轴 Z 轴相截， 截距系数之比为 2:∞:l，晶面符号为(102)；而晶面 e3之符号则为(10 2 )。除了这六个 晶面外，近于梯形的晶面一共还有六个，它们分别位于晶体的后面和左面，同理得 出它们的晶面符号。这样，12个近于梯形的晶面的晶面符号如下： (210)、（2 1 0）、（021）、(02 1 )、(102)、（10 2 ） ( 2 1 0)、（ 2 10）、（0 2 1 ）、(0 2 1)、( 1 0 2 )、（ 1 02） 在8个三角形晶面中，晶面 o1延展后将与三个结晶轴均相交，且三个截距系数值 也都相等，即为1:1:1，故其晶面符号为(111)。另外七个晶面的情况与 o1 类似，只是 与不同结晶轴截于正端或负端上有所差异。它们的晶面符号如下： （111）、（1 1 1）、（1 1 1 ）、（11 1 ） （ 1 1 1 ）、（ 1 1 1 ）、（ 1 11）、（ 1 1 1） 以上上下对着写的两个晶面符号，代表晶体上相互平行的一对晶面。 再例如单斜晶系的正长石晶体（图5-15)。其对称型为2/m(L2 PC)，我们以 L 2方向 作为结晶轴 Y 轴，以 m、a、b 等晶面的交棱方向为 Z 轴，而以 c、n、b 等晶面的 交棱方向为 X 轴；正长石晶体结构中相应方向上行列的重复周期，亦即晶胞的三根 棱长为 a=0.860nm，b=1.306nm，c=0.719nm，轴率 a:b:c=0.6585:1:0.5554。此时晶面 在三个结晶轴上的截距(指截距，不是指截距系数)之比为2.270:1.148:∞，则： h:k:l=0.6585/2.270:1/1.148:0.5554/∞=0.2904:0.8712:0=1:3:0 故正长石上晶面 a 之晶面符号为（130）。其他各晶面都可利用相同的关系式， 根据各自的截距比，求出相应的晶面符号