《结晶学》课程教学资源（教案讲义）第六章 单形和聚形

第六章单形和聚形在上一章中，我们建立了晶体的坐标系以及晶面符号和晶棱符号，并讨论了晶面和晶棱间的关系。这就使我们能够从简单的符号中获得关于晶体具体形状的基本信息。但是，晶面在晶体上的分布并不是彼此孤立的。晶面除了组成晶带以外，它们的分布还服从于晶体的对称特性。从晶面按对称规律组合的角度出发，于是就产生了单形和聚形的概念。同时还可由晶面符号衍生出单形符号。应用单形和聚形的概念以及单形符号来描述晶体的形态既简单又方便。一个实际晶体的外形，除决定于内因而使晶面呈对称分布，组成单形和聚形之外，它还必然会受到晶体生长过程中外界条件的影响，致使在不同条件下形成的同种晶体可能具有不同的形态特征：同时，晶体还会或多或少偏离理想形态形成歪晶，有时甚至还形成某些特殊的形态。此外，晶体生长过程中还会有某些痕迹保留在晶面上，形成晶面花纹。晶体的形态可分为两种类型：第一种：由同种晶面组成，称为单形（图6-1）：第二种，由两种以上的不同晶面组成，称为聚形（图6-2）。001001111010100010100图6-1单形（a-立方体：b-八面体）图6-2聚形（立方体和八面体相聚）此外，属于同一对称型的晶体，可以具有完全不同的形态，例如，立方体和八面体，对称型可以同为3L*4L’6L29PC，但形态完全不同。再如，对称型为3L?3PC的晶体，形态也可以完全不同。在这一章中，我们将讨论晶体的理想形态一单形和聚形。72

72 第六章 单形和聚形 在上一章中，我们建立了晶体的坐标系以及晶面符号和晶棱符号，并讨论了晶 面和晶棱间的关系。这就使我们能够从简单的符号中获得关于晶体具体形状的基本 信息。 但是，晶面在晶体上的分布并不是彼此孤立的。晶面除了组成晶带以外，它们 的分布还服从于晶体的对称特性。从晶面按对称规律组合的角度出发，于是就产生 了单形和聚形的概念。同时还可由晶面符号衍生出单形符号。应用单形和聚形的概 念以及单形符号来描述晶体的形态既简单又方便。 一个实际晶体的外形，除决定于内因而使晶面呈对称分布，组成单形和聚形之 外，它还必然会受到晶体生长过程中外界条件的影响，致使在不同条件下形成的同 种晶体可能具有不同的形态特征；同时，晶体还会或多或少偏离理想形态形成歪晶， 有时甚至还形成某些特殊的形态。此外，晶体生长过程中还会有某些痕迹保留在晶 面上，形成晶面花纹。 晶体的形态可分为两种类型：第一种：由同种晶面组成，称为单形（图6-1）；第 二种，由两种以上的不同晶面组成，称为聚形（图6-2）。 a b 图6-1 单形（a-立方体；b-八面体） 图6-2 聚形（立方体和八面体相聚） 此外，属于同一对称型的晶体，可以具有完全不同的形态，例如，立方体和八 面体，对称型可以同为 3L4 4L3 6L2 9PC，但形态完全不同。再如，对称型为 3L2 3PC 的晶体，形态也可以完全不同。 在这一章中，我们将讨论晶体的理想形态—单形和聚形

第一节单形的概念和单形符号一、单形的概念：晶体上相互间能够对称重复的一组晶面组合在一起，便构成一个单形。所以。同一单形中的各个晶面，彼此间必定都可以借助于对称要素的作用而相互重复，图6-3是斜方晶系的一个单形，它的八个晶面相互间都可以通过3L3PC对称型的作用发生重复。显然，同一单形的各个晶面，它们321321对于相同对称要素的关系（平行、垂直、以某个角度相交等)应该都是一致的。1,321321由于在晶体定向时我们总是优先选择对V-32T32T称要素作为结晶轴，即便在没有对称要1素可选时，也总是使结晶轴的安置符合/32T321于晶体本身的对称性，因此，对于同一个单形的各个晶面而言，它们与相同结晶轴之间的关系也应该都是一样的，即图6-3斜方双锥单形（对称形3L*3PC）它们在三个结晶轴上将具有相同的截距比，从而它们晶面指数的绝对值也必定相等。如图6-3。其8个晶面的晶面符号是：(321)、(321)351)（321)（32i)(321)（35i)（32i)。通过上面的分析，可以得出单形的概念：单形是借对称要素连系起来的一组晶面的总和。因此，单形具有以下特点：(1）同一单形的各个晶面必能相互对称重复。（2）在理想条件下，同一单形的所有晶面应是同形等大的。(3）各晶面与对称要素的关系是一致的。二、单形符号对于同一单形的各个晶面来说，它们的晶面指数之间都具有上述对称相等的关系。因此，有可能在同一单形的各个晶面中，按照一定的原则选择一个代表晶面，将它的晶面指数置于大括号中，写成hkl，用以代表整个单形的所有晶面，这种符号称为单形符号。选择代表晶面必须遵循一定的原则，其总原则是：（1）代表晶面应选择正指数最多的晶面，至少要尽可能选择1为正值者。(2）在上述前提下，对中级晶族，尽可能使h≥k，高级晶族：h≥k≥l。为满足上述总的原则，根据各晶族的对称特点和选轴原则，得出选择代表晶面的具体法则：（1）在高级晶族中，按先前、次右、后上的法则选择代表晶面。(2）中低级晶族，按先上、次前、后右的法则。73

73 第一节 单形的概念和单形符号 一、单形的概念： 晶体上相互间能够对称重复的一组晶面组合在一起，便构成一个单形。所以。 同一单形中的各个晶面，彼此间必定都可以借助于对称要素的作用而相互重复，图 6-3是斜方晶系的一个单形，它的八个晶面相互间都可以通过3L2 3PC对称型的作用发 生重复。 显然，同一单形的各个晶面，它们 对于相同对称要素的关系(平行、垂直、 以某个角度相交等)应该都是一致的。 由于在晶体定向时我们总是优先选择对 称要素作为结晶轴，即便在没有对称要 素可选时，也总是使结晶轴的安置符合 于晶体本身的对称性，因此，对于同一 个单形的各个晶面而言，它们与相同结 晶轴之间的关系也应该都是一样的，即 图6-3 斜方双锥单形（对称形3L2 3PC） 它们在三个结晶轴上将具有相同的截距 比，从而它们晶面指数的绝对值也必定相等。如图6-3。其8个晶面的晶面符号是： （321）、（3 2 1）、（ 3 2 1）、（ 3 21）、（32 1 ）、（3 2 1 ）、（ 3 2 1 ）、（ 3 2 1 ）。 通过上面的分析，可以得出单形的概念：单形是借对称要素连系起来的一组晶 面的总和。因此，单形具有以下特点： ⑴ 同一单形的各个晶面必能相互对称重复。 ⑵ 在理想条件下，同一单形的所有晶面应是同形等大的。 ⑶ 各晶面与对称要素的关系是一致的。 二、单形符号 对于同一单形的各个晶面来说，它们的晶面指数之间都具有上述对称相等的关 系。因此，有可能在同一单形的各个晶面中，按照一定的原则选择一个代表晶面， 将它的晶面指数置于大括号中，写成{hkl}，用以代表整个单形的所有晶面，这种符 号称为单形符号。 选择代表晶面必须遵循一定的原则，其总原则是： ⑴ 代表晶面应选择正指数最多的晶面，至少要尽可能选择 l 为正值者。 ⑵ 在上述前提下，对中级晶族，尽可能使 h≥k，高级晶族：h≥k≥l。 为满足上述总的原则，根据各晶族的对称特点和选轴原则，得出选择代表晶面 的具体法则： ⑴ 在高级晶族中，按先前、次右、后上的法则选择代表晶面。 ⑵ 中低级晶族，按先上、次前、后右的法则

前、右、上的标准：三轴定向中，分别以X、Y、Z轴的正端为前、右、上。四轴定向中，以X正端和U负端的分角线方向为前，Y正端为右，Z正端为上。在这里，选择“前、右、上”，实际上是意味着使三个晶面指数尽量为正：在中、低级晶族中“先上”，就是尽可能使1为正，“次前、后右”的顺序则是为了尽可能使h≥k。高级晶族中由于对称特点决定，1为正是必定可以保证的，而“先前、次右、后上”的顺序则是为了尽可能满足h≥k≥1。不过，这种形象化的选择法则，在很少情况下（主要是对于实际晶体中罕见的某些单形)也可能与总的原则不完全符合而不能适用。图6-4为四方晶系的一个单形。在它的16个晶面中，先上，包括图b顶视图中所示的8个晶面：次前，在以上8个面之中最朝前的为（321）和（321）两个：后右，便只剩下(321)。因此，其单形符号应为(321)。图6-5则为等轴晶系的一个单形，由48个对称相同的晶面组成。“先前”，同等程度地最朝前的晶面共有8个，即它们的指数在图中用黑体学注出者：“次右”，这8个面中最偏右的将是(321)、（32i)两者：“后上”，即(321)。于是，其单形符号便是(321)。在图6-3斜方晶系单形的例子中，其单形符号恰好也是(321)。123V21323132321132132317321237323231/321322312332123TX32123121328123113212351b图6-4四方双锥单形代表晶面的选择图6-5六八面体单形代表晶面的选择a-体视图：b-顶视图从以上三个例子可以发现，对于同一单形的各个晶面而言，它们彼此间指数的绝对值肯定是相等的，但不同数字的指数在晶面符号中排列的顺序却有的不变，有的可变。之所以存在这种差别，其根源是在于它们的对称程度有差异。在高级晶族中，晶体的三个结晶轴必定能通过晶体所固有的4L之作用而相互重复，亦即三个结晶轴的性质都是相同的。因此，假若有一晶面在三个结晶轴上的截距依次为pa、qa、ra时，则绕L旋转120°后，必定有另一截距为qa、ra、pa的晶面与之对称重复：再旋转120°后，还会有截距为ra、pa、qa的晶面也发生重复。显然，这些晶面都应属于同一单形，它们晶面指数的排列顺序则是全部可以轮换的，例如图6-5所示单形中的（321）、（213）、（132)等。在中级晶族中，由于各水平结晶轴之间必能借助于晶体中唯一的高次轴之作用而相互对称重复，亦即各水平结晶轴的性质是相同的，但它们与轴之间则无对称联系，因此，属于同一单形的各个晶面，它们对74

74 前、右、上的标准：三轴定向中，分别以X、Y、Z轴的正端为前、右、上。四 轴定向中，以X正端和U负端的分角线方向为前，Y正端为右，Z正端为上。 在这里，选择“前、右、上”，实际上是意味着使三个晶面指数尽量为正；在中、 低级晶族中“先上”，就是尽可能使l为正，“次前、后右”的顺序则是为了尽可能使h≥k。 高级晶族中由于对称特点决定，l为正是必定可以保证的，而“先前、次右、后上”的 顺序则是为了尽可能满足h≥k≥l。不过，这种形象化的选择法则，在很少情况下(主 要是对于实际晶体中罕见的某些单形)也可能与总的原则不完全符合而不能适用。 图6-4为四方晶系的一个单形。在它的16个晶面中，先上，包括图b顶视图中所示 的8个晶面；次前，在以上8个面之中最朝前的为(3 2 1)和(321)两个；后右，便只剩下 (321)。因此，其单形符号应为{321}。 图6-5则为等轴晶系的一个单形，由48个对称相同的晶面组成。“先前”，同等程 度地最朝前的晶面共有8个，即它们的指数在图中用黑体字注出者；“次右”，这8个 面中最偏右的将是(321)、(32 1 )两者；“后上”，即(321)。于是，其单形符号便是{321}。 在图6-3斜方晶系单形的例子中，其单形符号恰好也是{321}。 a b 图6-4 四方双锥单形代表晶面的选择 图6-5 六八面体单形代表晶面的选择 a-体视图；b-顶视图 从以上三个例子可以发现，对于同一单形的各个晶面而言，它们彼此间指数的 绝对值肯定是相等的，但不同数字的指数在晶面符号中排列的顺序却有的不变，有 的可变。之所以存在这种差别，其根源是在于它们的对称程度有差异。 在高级晶族中，晶体的三个结晶轴必定能通过晶体所固有的4L 3之作用而相互重 复，亦即三个结晶轴的性质都是相同的。因此，假若有一晶面在三个结晶轴上的截 距依次为pa、qa、ra时，则绕L 3旋转120 o后，必定有另一截距为qa、ra、pa的晶面与 之对称重复；再旋转120 o后，还会有截距为ra、pa、qa的晶面也发生重复。显然，这 些晶面都应属于同一单形，它们晶面指数的排列顺序则是全部可以轮换的，例如图 6-5所示单形中的(321)、(213)、(132)等。在中级晶族中，由于各水平结晶轴之间必 能借助于晶体中唯一的高次轴之作用而相互对称重复，亦即各水平结晶轴的性质是 相同的，但它们与Z轴之间则无对称联系，因此，属于同一单形的各个晶面，它们对

应于乙轴的指数在符号中的排列顺序不能改变。而对应于水平结晶轴的指数则可以相互掉换排列顺序。图6-4的例子就属于这种情况。最后，在低级晶族中，由于三个结晶轴彼此间全都不能由对称要素相联系，因此，属于同一单形的各个晶面。其指数的排列顺序就不充许有丝毫改变，否则，就肯定不属于同一个单形。在此可以顺便指出，为什么在三方和六方晶系中我们要采用四轴定向，亦即要选取三个水平结晶轴，尽管从数学的角度来看。有两个水平结晶轴就已够了。例如电气石晶体的例子中，（10i0)、（i100)、（0i10)三个晶面组成一个三方柱的单形，在这三个晶面中，指数间的对称关系是显而易见的。但如果我们采用三个结晶轴，取消U轴，那么。这三个晶面的符号将成为(100)、（i10)、（0i0），结果使得属于同一单形的各晶面之间，无法从指数上反映出对称关系来，从而也给单形符号的建立造成了困难。第二节146种结晶单形的导出由单形的概念可知，以单形中的任意一晶面作原始晶面，通过该对称型中全部对称要素的作用，必能导出该单形的全部晶面。不同的对称型，由于对称要素的数目和种类不同，将导出不同的单形。在同一对称型中，由于原始晶面与对称要素的相对位置关系不同，所导出的单形也不同。现以L*和L2P对称型为例，说明单形的推导过程。四方晶系的L对称型中，唯一的L*为Z轴。晶面与L之间的可能关系不外乎垂直、平行和斜交三种情况。bac图6-6导出L4对称型单形的示意图a-单面(001)：b-四方柱（100)：c-四方单锥(hhl)(1）原始晶面与L4（Z轴）垂直，而与X、Y轴平行。它通过此L*的作用，始终只能与自身相重复，因此，单独这样一个晶面就构成一个单形，称为单面，其单形75

75 应于Z轴的指数在符号中的排列顺序不能改变。而对应于水平结晶轴的指数则可以相 互掉换排列顺序。图6-4的例子就属于这种情况。最后，在低级晶族中，由于三个结 晶轴彼此间全都不能由对称要素相联系，因此，属于同一单形的各个晶面。其指数 的排列顺序就不允许有丝毫改变，否则，就肯定不属于同一个单形。 在此可以顺便指出，为什么在三方和六方晶系中我们要采用四轴定向，亦即要 选取三个水平结晶轴，尽管从数学的角度来看。有两个水平结晶轴就已够了。例如 电气石晶体的例子中，(10 1 0)、( 1 100)、(0 1 10)三个晶面组成一个三方柱的单形，在 这三个晶面中，指数间的对称关系是显而易见的。但如果我们采用三个结晶轴，取 消U轴，那么。这三个晶面的符号将成为(100)、( 1 10)、（0 1 0），结果使得属于同一 单形的各晶面之间，无法从指数上反映出对称关系来，从而也给单形符号的建立造 成了困难。 第二节 146 种结晶单形的导出 由单形的概念可知，以单形中的任意一晶面作原始晶面，通过该对称型中全部 对称要素的作用，必能导出该单形的全部晶面。不同的对称型，由于对称要素的数 目和种类不同，将导出不同的单形。在同一对称型中，由于原始晶面与对称要素的 相对位置关系不同，所导出的单形也不同。 现以 L 4 和 L 2 2P 对称型为例,说明单形的推导过程。 四方晶系的L 4对称型中，唯一的L 4为Z轴。晶面与L 4之间的可能关系不外乎垂直、 平行和斜交三种情况。 a b c 图6-6 导出L 4对称型单形的示意图 a-单面{001}；b-四方柱{100}；c-四方单锥{hhl} ⑴ 原始晶面与L 4（Z轴）垂直，而与X、Y轴平行。它通过此L 4的作用，始终 只能与自身相重复，因此，单独这样一个晶面就构成一个单形，称为单面，其单形

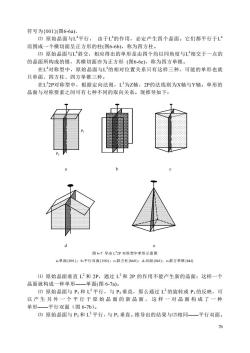
符号为(001)(图6-6a)，(2）原始晶面与L4平行，由于L*的作用，必定产生四个晶面。它们都平行于L4而围成一个横切面呈正方形的柱（图6-6b），称为四方柱。（3）原始晶面与L4斜交，相应得出的单形是由四个均以同角度与L4相交于一点的的晶面所构成的锥，其横切面亦为正方形（图6-6c)，称为四方单锥。在L对称型中，原始晶面与L的相对位置关系只有这样三种，可能的单形也就只单面、四方柱、四方单锥三种。在L-2P对称型中，根据定向法则，L-为Z轴，2P的法线则为X轴与Y轴。单形的晶面与对称要素之间可有七种不同的取向关系。现推导如下：P,baCd?图6-7导出L?2P对称型中单形示意图a-单面(001)：b-平行双面（100)：c-斜方柱（hk0)：d-双面(0kl)：e-斜方单锥（hkl)（1）原始晶面垂直L?和2P，通过L?和2P的作用不能产生新的晶面：这样一个晶面就构成一种单形——单面(图6-7a)。(2）原始晶面与Pi和L2平行，与P2垂直，那么通过L的旋转或Pi的反映，可以产生另外一个平行于原始晶面的新晶面，这样一对晶面构成了一种单形一一平行双面（图6-7b）。(3）原始晶面与P2和L?平行，与PI垂直。推导出的结果与(2)相同一一平行双面。76

76 符号为{001}(图6-6a)， ⑵ 原始晶面与L 4平行， 由于L 4的作用，必定产生四个晶面。它们都平行于L 4 而围成一个横切面呈正方形的柱(图6-6b)，称为四方柱。 ⑶ 原始晶面与L 4斜交，相应得出的单形是由四个均以同角度与L 4相交于一点的 的晶面所构成的锥，其横切面亦为正方形 (图6-6c)，称为四方单锥。 在L 4对称型中，原始晶面与L 4的相对位置关系只有这样三种，可能的单形也就 只单面、四方柱、四方单锥三种。 在L 2 2P对称型中，根据定向法则，L 2为Z轴，2P的法线则为X轴与Y轴。单形的 晶面与对称要素之间可有七种不同的取向关系。现推导如下： P1 P2 a b c d e 图 6-7 导出 L 2 2P 对称型中单形示意图 a-单面{001}；b-平行双面{100}；c-斜方柱{hk0}；d-双面{0kl}；e-斜方单锥{hkl} ⑴ 原始晶面垂直 L 2 和 2P，通过 L 2 和 2P 的作用不能产生新的晶面；这样一个 晶面就构成一种单形——单面(图 6-7a)。 ⑵ 原始晶面与 P1 和 L 2 平行，与 P2 垂直，那么通过 L 2 的旋转或 P1 的反映，可 以 产 生 另 外 一 个 平 行 于 原 始 晶 面 的 新 晶 面 ， 这 样 一 对 晶 面 构 成 了 一 种 单形——平行双面（图 6-7b）。 ⑶ 原始晶面与 P2 和 L 2 平行，与 P1 垂直。推导出的结果与⑵相同——平行双面

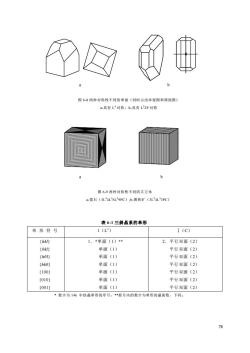
(4）原始晶面与L2平行，与2P斜交，通过L2的旋转或2P的反映，可以导出四个晶面，这四个晶面围成一个平行于L柱，柱的横截面为菱形，它们组成一种新的单形一一斜方柱（图6-7c）。(5）原始晶面与L和P，斜交，与P2垂直，由于L的旋转或P的反映，可以产生一个与原始晶面斜交的新晶面。这两个晶面便组成了一个新单形一一双面（图6-7d)。(6)原始晶面与L和P2斜交，与P,垂直，导出的结果与(5)相同一一双面。(7）原始晶面与L和2P均斜交，通过L?和P的作用可以获得四个以同一角度交L于一点的晶面，这四个晶面围成一个横截面为菱形的锥，由此构成一种新的单形一一斜方单锥（图6-7e）。综上所述，在L2P对称型中，原始晶面与对称要素的相对位置关系有七种，共推导出五种单形（除去重复的）：单面、平行双面、双面、斜方柱、斜方单锥。在每一种对称型中，单形晶面与对称要素的相对位置关系最多仅有七种。因此每一种对称型至多只能导出七种单形。如果对32种对称型逐一进行推导，最终将导出146种不同的单形。这是所有晶体中所能出现的全部单形，称结晶单形。146种单形在各晶系中的分布及相应的单形符号如表6-1至表6-13所列（表中形号一栏，对于指数可能取负值的情况没有单独列出。其单形相同于指数为正值的情况。例如L3P对称型中，（000i）与（0001相同，亦为单面）。早先，对于单形还有另外的一些命名，不过其中只有轴面这一名称目前还被广泛应用。轴面是指只与一个结晶轴相交而与其余结晶轴均平行的板面或单面：其中单形符号为0011或者（00011者特别称为底轴面。必须强调指出，在不同的对称型中，甚或在不同的晶系以至不同的晶族中，虽然可能出现几何上相同的单形，亦即命名相同的单形，但它们在对称性上必定存在有差异。因此，上述的146种单形都是结晶学上不同的单形。例如，在前述的L*和L?2P两个对称型中都可以有单面出现，两者都由单独一个晶面组成，但这两种单面一个是垂直于唯一的L4，另一个则是同时垂直于L和2P。所以，当它们在晶体中出现时，两者的晶面形状就会有本质上的差异，而各自与本身的对称性相符（见图6-8）。再如立方体，它在等轴晶系的全部五个对称型中都可出现。如果单纯从几何外形上讲，任何立方体都应该具有3L*4L6L-9PC对称型，但从结晶学的意义上讲，亦即全面地考虑到各方面的性质，例如生长时在晶面上留下的细微花纹的对称性。物理性质所表现出来的对称性等等，则五个对称型中的五种立方体，它们的对称特点都是不同的，分别与各自的对称型相适应。所以，它们是五种结晶学上不同的单形。图6-9分别示出了萤石（对称型为3L*4L6L29PC）和黄铁矿（对称型为3L?4L3PC)的立方体，它们晶面上的条纹方向指示了它们各自的真实对称。当然。有些黄铁矿的立方体晶体并不表现出条纹。但这绝不意味着此时黄铁矿立方体的对称性就提高了，它的真实对称仍是3L-4L?3PC，而在几何外形上所表现出来的3L*4L6L-9PC对称则是一种假象。77

77 ⑷ 原始晶面与 L 2 平行，与 2P 斜交，通过 L 2 的旋转或 2P 的反映，可以导出四 个晶面，这四个晶面围成一个平行于 L 2 柱，柱的横截面为菱形，它们组成一种新的 单形——斜方柱（图 6-7c）。 ⑸ 原始晶面与 L 2 和 P1 斜交，与 P2 垂直，由于 L 2 的旋转或 P 的反映，可以产 生一个与原始晶面斜交的新晶面。这两个晶面便组成了一个新单形——双面（图 6-7d）。 ⑹原始晶面与 L 2 和 P2 斜交，与 P1 垂直，导出的结果与⑸相同——双面。 ⑺ 原始晶面与 L 2 和 2P 均斜交，通过 L 2 和 P 的作用可以获得四个以同一角度交 L 2 于一点的晶面，这四个晶面围成一个横截面为菱形的锥，由此构成一种新的单形 ——斜方单锥（图 6-7e）。 综上所述，在 L 2 2P 对称型中，原始晶面与对称要素的相对位置关系有七种，共 推导出五种单形（除去重复的）：单面、平行双面、双面、斜方柱、斜方单锥。 在每一种对称型中，单形晶面与对称要素的相对位置关系最多仅有七种。因此， 每一种对称型至多只能导出七种单形。如果对 32 种对称型逐一进行推导，最终将导 出 146 种不同的单形。这是所有晶体中所能出现的全部单形，称结晶单形。 146种单形在各晶系中的分布及相应的单形符号如表6-1至表6-13所列 (表中形 号一栏，对于指数可能取负值的情况没有单独列出。其单形相同于指数为正值的情 况。例如L 3 3P对称型中，{000 1 }与{0001}相同，亦为单面)。 早先，对于单形还有另外的一些命名，不过其中只有轴面这一名称目前还被广 泛应用。轴面是指只与一个结晶轴相交而与其余结晶轴均平行的板面或单面；其中 单形符号为{001}或者{0001}者特别称为底轴面。 必须强调指出，在不同的对称型中，甚或在不同的晶系以至不同的晶族中，虽 然可能出现几何上相同的单形，亦即命名相同的单形，但它们在对称性上必定存在 有差异。因此，上述的146种单形都是结晶学上不同的单形。 例如，在前述的L 4和L 2 2P两个对称型中都可以有单面出现，两者都由单独一个 晶面组成，但这两种单面一个是垂直于唯一的L 4，另一个则是同时垂直于L 2和2P。 所以，当它们在晶体中出现时，两者的晶面形状就会有本质上的差异，而各自与本 身的对称性相符（见图6-8）。 再如立方体，它在等轴晶系的全部五个对称型中都可出现。如果单纯从几何外 形上讲，任何立方体都应该具有3L4 4L3 6L2 9PC对称型，但从结晶学的意义上讲，亦 即全面地考虑到各方面的性质，例如生长时在晶面上留下的细微花纹的对称性。物 理性质所表现出来的对称性等等，则五个对称型中的五种立方体，它们的对称特点 都是不同的，分别与各自的对称型相适应。所以，它们是五种结晶学上不同的单形。 图6-9分别示出了萤石（对称型为3L4 4L3 6L2 9PC）和黄铁矿（对称型为3L2 4L3 3PC)的 立方体，它们晶面上的条纹方向指示了它们各自的真实对称。当然。有些黄铁矿的 立方体晶体并不表现出条纹。但这绝不意味着此时黄铁矿立方体的对称性就提高了， 它的真实对称仍是3L2 4L3 3PC，而在几何外形上所表现出来的3L4 4L3 6L2 9PC对称则是 一种假象

ba图6-8两种对称性不同的单面（同时示出体视图和顶视图）a-具有L*对称：b-具有L?2P对称1a图6-9两种对称性不同的立方体a-萤石（3L*4L*6L?9PC）b-黄铁矿（3L*4L3PC）表6-1三斜晶系的单形1 (L')单形符号i(c)(hkl)1.*单面（1）**2.平行双面（2)单面（1)平行双面（2)(ok))单面（1)(hon)平行双面（2）单面（1)(hko)平行双面（2)单面（1)平行双面（2)(100)单面（1)平行双面（2)(010)单面（1)平行双面（2)(001)*数字为146中结晶单形的序号：**括号内的数字为单形的晶面数，下同。78

78 a b 图 6-8 两种对称性不同的单面（同时示出体视图和顶视图） a-具有 L 4 对称；b-具有 L 2 2P 对称 a b 图 6-9 两种对称性不同的立方体 a-萤石（3L4 4L3 6L2 9PC）;b-黄铁矿（3L2 4L3 3PC） 表 6-1 三斜晶系的单形 单 形 符 号 1（L 1） 1 （C） {hkl} {0kl} {h0l} {hk0} {100} {010} {001} 1．*单面（1）** 单面（1） 单面（1） 单面（1） 单面（1） 单面（1） 单面（1） 2．平行双面（2） 平行双面（2） 平行双面（2） 平行双面（2） 平行双面（2） 平行双面（2） 平行双面（2） * 数字为 146 中结晶单形的序号；**括号内的数字为单形的晶面数，下同

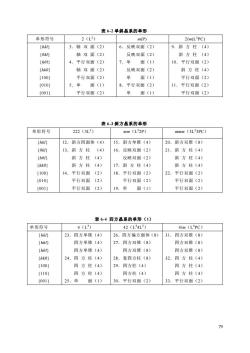
表6-2单斜晶系的单形2 (L2)单形符号m(P)2/m(L°PC)(hkl)9.斜方柱（4)3.轴双面（2)6.反映双面（2）轴双面（2)反映双面(2)斜方柱（4)(Okl)7.单面(1)(hon)4.平行双面（2）10.平行双面（2）轴双面（2)斜方柱（4)(hko)反映双面（2)单面(1)(100)平行双面（2)平行双面（2)5. 单面(1)8.平行双面（2)(010)11.平行双面（2）单平行双面（2)面(1)平行双面（2)(001)表6-3斜方晶系的单形222 (3L2)单形符号mm(L22P)mmm（3L23PC)12.斜方四面体（4）15.斜方单锥（4）20.斜方双锥（8）(hkl)13.斜方柱(4)16.反映双面（2）21.斜方柱（4)(Okl)(ho)斜方柱（4)反映双面（2)斜方柱（4）斜方柱(4)17.斜方柱（4）斜方柱（4)(hko)(100)14.平行双面(2)18.平行双面（2）22.平行双面（2）(2)平行双面（2）(010)平行双面平行双面（2）19.单平行双面(2)面(1)平行双面（2)(001)表6-4四方晶系的单形（1)4 (L*)42 (L*4L2)4/m (LpC)单形符号23四方单锥（4)26.四方偏方面体（8）四方双锥（8）(hkl)31.四方单锥（4）四方双锥（8）(hhl)27.四方双锥（8）(hol)四方单锥（4）四方双锥（8）四方双锥（8）(hko)24.四方柱（4)28.复四方柱（8）32.四方柱（4）(100)四方柱（4)29.四方柱（4）四方柱（4)(110)四方柱（4)四方柱（4）四方柱（4)25.单面(1)(001)30.平行双面（2）33.平行双面（2）79

79 表 6-2 单斜晶系的单形 单形符号 2（L 2） m(P) 2/m(L2 PC) {hkl} {0kl} {h0l} {hk0} {100} {010} {001} 3．轴 双 面（2） 轴 双 面（2） 4．平行双面（2） 轴 双 面（2） 平行双面（2） 5．单 面（1） 平行双面（2） 6．反映双面（2） 反映双面（2） 7．单 面（1） 反映双面（2） 单 面（1） 8．平行双面（2） 单 面（1） 9．斜 方 柱 （4） 斜 方 柱 （4） 10．平行双面（2） 斜 方 柱（4） 平行双面（2） 11．平行双面（2） 平行双面（2） 表 6-3 斜方晶系的单形 单形符号 222（3L2） mm（L 2 2P） mmm（3L2 3PC） {hkl} {0kl} {h0l} {hk0} {100} {010} {001} 12．斜方四面体（4） 13．斜 方 柱 （4） 斜 方 柱 （4） 斜 方 柱 （4） 14．平行双面 （2） 平行双面 （2） 平行双面 （2） 15．斜方单锥（4） 16．反映双面（2） 反映双面（2） 17．斜 方 柱（4） 18．平行双面（2） 平行双面（2） 19．单 面（1） 20．斜方双锥（8） 21．斜 方 柱（4） 斜 方 柱（4） 斜 方 柱（4） 22．平行双面（2） 平行双面（2） 平行双面（2） 表 6-4 四方晶系的单形（1） 单形符号 4（L 4） 42（L 4 4L2） 4/m（L 4 PC） {hkl} {hhl} {h0l} {hk0} {100} {110} {001} 23．四方单锥（4） 四方单锥（4） 四方单锥（4） 24．四 方 柱（4） 四 方 柱（4） 四 方 柱（4） 25．单 面（1） 26．四方偏方面体（8） 27．四方双锥（8） 四方双锥（8） 28．复四方柱（8） 29．四方柱（4） 四方柱（4） 30．平行双面（2） 31．四方双锥（8） 四方双锥（8） 四方双锥（8） 32．四 方 柱（4） 四 方 柱（4） 四 方 柱（4） 33．平行双面（2）

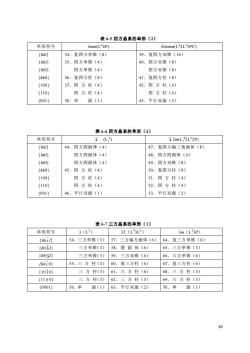
表6-5四方晶系的单形（2）单形符号4mm(L'4P)4/mmm(L*4L*5PC)(hkl)34.复四方单锥（8）复四方双锥（16）39.(hhl)35.四方单锥（4）40.四方双锥（8）(hon)四方单锥（4）四方双锥（8）36.复四方柱（8）41.复四方柱（8）(hko)(100)37.四方柱（4)42.四方柱（4）四方柱（4)(110)四方柱（4)38.单面(1)[001)43.平行双面（2）表6-6四方晶系的单形（3）4(L)单形符号42m(L;2L*2P)(hkl)44.四方四面体（4）47：复四方偏三角面体（8）四方四面体（4）48.四方四面体（4）(hhl)49.四方双锥（8）(hol)四方四面体（4）(hko)45.四方柱（4）50.复四方柱（8）(100)四方柱（4)51.四方柱（4)四方柱（4)(110)52四方柱（4)46.平行双面（1)53.平行双面（2)(001)表6-7三方晶系的单形（1）3 (L*)32 (L'3L2)单形符号3m(L*3P)54.三方单锥（3）(hkin)57.三方偏方面体（6）64.复三方单锥（6）(hohi)三方单锥（3）58.菱面体（6)65.三方单锥（3)(hhz])三方单锥（3）59.三方双锥（6)66.六方单锥（6）55.三方柱（3）60.复三方柱（6)67.复三方柱（6）(hkio)(10i0)三方柱（3）61.六方柱（6)68.三方柱（3)三方柱（3)62.三方柱（3)(1120)69.六方柱（3)56.单(0001)面(1)70.单面(1)63.平行双面（2)80

80 表 6-5 四方晶系的单形（2） 单形符号 4mm(L4 4P) 4/mmm(L4 4L2 5PC) {hkl} {hhl} {h0l} {hk0} {100} {110} {001} 34．复四方单锥（8） 35．四方单锥（4） 四方单锥（4） 36．复四方柱（8） 37．四 方 柱（4） 四 方 柱（4） 38．单 面（1） 39．复四方双锥（16） 40．四方双锥（8） 四方双锥（8） 41．复四方柱（8） 42．四 方 柱（4） 四 方 柱（4） 43．平行双面（2） 表 6-6 四方晶系的单形（3） 单形符号 4 (Li 4 ) 4 2m(Li 4 2L2 2P) {hkl} {hhl} {h0l} {hk0} {100} {110} {001} 44．四方四面体（4） 四方四面体（4） 四方四面体（4） 45．四 方 柱（4） 四 方 柱（4） 四 方 柱（4） 46．平行双面（1） 47．复四方偏三角面体（8） 48．四方四面体（4） 49．四方双锥（8） 50．复四方柱（8） 51．四 方 柱（4） 52．四 方 柱（4） 53．平行双面（2） 表 6-7 三方晶系的单形（1） 单形符号 3（L 3） 32（L 3 3L2） 3m（L 3 3P） {hk i l} 54．三方单锥（3） 57．三方偏方面体（6） 64．复三方单锥（6） {h0 h l} 三方单锥（3） 58．菱 面 体（6） 65．三方单锥（3） {hh 2h l} 三方单锥（3） 59．三方双锥（6） 66．六方单锥（6） {hk i 0} 55．三 方 柱（3） 60．复三方柱（6） 67．复三方柱（6） {10 1 0} 三 方 柱（3） 61．六 方 柱（6） 68．三 方 柱（3） {11 2 0} 三 方 柱（3） 62．三 方 柱（3） 69．六 方 柱（3） {0001} 56．单 面（1） 63．平行双面（2） 70．单 面（1）

表6-8三方晶系的单形（2）单形符号3 (L°c)3m(L°3L°3PC)(hkil)71.菱面体（6）74.复三方偏三角面体（12）(hohl)菱面体（6）75.菱面体（6)(hhzal)菱面体（6)76.六方双锥（12)(hki0)72.六方柱（6)77.复六方柱（12）(10i0)六方柱（678.六方柱（6)(1120)六方柱（6）79.六方柱（6)(0001)73.单面(1)80.平行双面（2）表6-9六方晶系的单形(1)单形符号6 (L6)62 (L6L2)6/m (L°PC)(hkil)81.六方单锥（6)84.六方偏方面体（6）89.六方双锥（12）(hOhl)六方单锥（6)85.六方双锥（12）六方双锥（12)(hhzal)六方单锥（6)六方双锥（12)六方双锥（12）(hkio)六方柱（6)复六方柱（12)90.六方柱（6)82.86.六方柱（6)87.六方柱（6)六方柱（6)(10i0)(1120)六方柱（6)六方柱（3)六方柱（6)83.单面(1)91.平行双面（2)(0001)88.平行双面（2）表6-10六方晶系的单形(2)单形符号6mm(L°6P)6/mmm(L°6L27PC)97.(hkin)92.复六方单锥（12）复六方双锥（24）(hohi)93.六方单锥（6)98.六方双锥（12)(hhzl)六方单锥（6）六方双锥（12）(hki0)复六方柱（12）99.复六方柱（12）94.(10i0)95.六方柱（6)100.六方柱（6)(1120)六方柱（6)六方柱（6)96.单面(1)(0001)101.平行双面（2）81

81 表 6-8 三方晶系的单形（2） 单形符号 3 (L3C) 3 m(L3 3L2 3PC) {hk i l} 71．菱面体（6） 74．复三方偏三角面体（12） {h0 h l} 菱面体（6） 75．菱面 体（6） {hh 2h l} 菱面体（6） 76．六方双锥（12） {hk i 0} 72．六方柱（6） 77．复六方柱（12） {10 1 0} 六方柱（6） 78．六 方 柱（6） {11 2 0} 六方柱（6） 79．六 方 柱（6） {0001} 73．单 面（1） 80．平行双面（2） 表 6-9 六方晶系的单形(1) 单 形符号 6（L 6） 62（L 6 6L2） 6/m（L 6 PC） {hk i l} 81．六方单锥（6） 84．六方偏方面体（6） 89．六方双锥（12） {h0 h l} 六方单锥（6） 85．六方双锥（12） 六方双锥（12） {hh 2h l} 六方单锥（6） 六方双锥（12） 六方双锥（12） {hk i 0} 82．六 方 柱（6） 86．复六方柱（12） 90．六 方 柱（6） {10 1 0} 六 方 柱（6） 87．六 方 柱（6） 六 方 柱（6） {11 2 0} 六 方 柱（6） 六 方 柱（3） 六 方 柱（6） {0001} 83．单 面（1） 88．平行双面（2） 91．平行双面（2） 表 6-10 六方晶系的单形(2) 单 形符号 6mm(L6 6P) 6/mmm(L6 6L2 7PC) {hk i l} 92．复六方单锥（12） 97． 复六方双锥（24） {h0 h l} 93．六方单锥（6） 98． 六方双锥（12） {hh 2h l} 六方单锥（6） 六方双锥（12） {hk i 0} 94．复六方柱（12） 99． 复六方柱（12） {10 1 0} 95．六 方 柱（6） 100．六 方 柱（6） {11 2 0} 六 方 柱（6） 六 方 柱（6） {0001} 96．单 面（1） 101．平行双面（2）