《结晶学》课程教学资源（教案讲义）第三章 晶体的面角恒等和投影

第三章晶体的面角恒等和投影根据晶体生长的布拉维法则，实际晶体往往为面网密度较大的面网所包围。同种晶体中，密度较大的面网是有限的，它们总是构成该种晶体不同个体的晶面。但是，由于受到复杂生长环境的影响，由相同面网形成的晶面在不同个体上的形态大小不同，形成歪晶（图3-1）。这掩盖了晶体的固有的对称性特点，给人类掌握晶体形态的规律带来困难。E图3-1石英晶体的不同实际形态面角r^m=141°47，m^m=120°，r^z=1349但科学家们后来发现，同种晶体的形态虽然随环境变化而变化，但对应晶面间的夹角不变，这就是面角恒等定律。在此基础上，人们开始测量晶面夹角，并根据测角数据进行晶面投影，从而恢复了晶体的理想形态。第一节面角恒等定律面角恒等定律是由丹麦矿物学家斯丹诺（N.Steno）于1669年首先提出，又称斯丹诺定律。它的主要内容是：同种晶体，对应晶面间的夹角恒等。面角：任意两晶面法线之间的夹角。其数值等于晶面夹角的补角。晶面夹角恒等，面角当然恒等。如图3-2所示,AC、CB为两相交晶面，α为两晶面的夹角，β为两晶面的面角。图3-1中所示的三个石英晶体，均由相同的晶面组成，晶面的形状大小不同晶体25

25 第三章 晶体的面角恒等和投影 根据晶体生长的布拉维法则，实际晶体往往为面网密度较大的面网所包围。同 种晶体中，密度较大的面网是有限的，它们总是构成该种晶体不同个体的晶面。但 是，由于受到复杂生长环境的影响，由相同面网形成的晶面在不同个体上的形态大 小不同，形成歪晶（图 3-1）。这掩盖了晶体的固有的对称性特点，给人类掌握晶体 形态的规律带来困难。 图 3-1 石英晶体的不同实际形态 面角 r∧m=141°47′，m∧m=120°，r∧z=134° 但科学家们后来发现，同种晶体的形态虽然随环境变化而变化，但对应晶面间 的夹角不变，这就是面角恒等定律。在此基础上，人们开始测量晶面夹角，并根据 测角数据进行晶面投影，从而恢复了晶体的理想形态。 第一节 面角恒等定律 面角恒等定律是由丹麦矿物学家斯丹诺（N.Steno）于 1669 年首先提出，又称斯 丹诺定律。它的主要内容是：同种晶体，对应晶面间的夹角恒等。 面角：任意两晶面法线之间的夹角。其数值等于晶面夹角的补角。晶面夹角恒 等，面角当然恒等。如图 3-2 所示,AC、CB 为两相交晶面，α 为两晶面的夹角，β 为 两晶面的面角。 图 3-1 中所示的三个石英晶体，均由相同的晶面组成，晶面的形状大小不同晶体

的外形自然也不一样，但是对应晶面间的夹角完全相等。面角恒等是格子构造的必然结果。因为同种晶体具有完全相同的格子构造，格子构造中的同种面网构成晶体外形上的同种晶面。晶11体生长过程中，晶面平行向外推移，故不论A晶面大小形态如何，对应晶面间的夹角恒定不变。面角恒等定律的发现，对结晶学的发展有深远的影响，使人类从千变万化的实际晶0体中找出了同种晶体外形上的固有规律，并用面角测量和投影的方法，恢复晶体的理想图3-2晶面夹角和面角形态，奠定了几何结晶学的基础。第二节晶体测量由面角恒等定律可知，只要知道了各晶面间的面角关系，就有可能恢复晶体的理想几何外形。为此，需要实际测量晶面之间的夹角，以获得面角数据。这项工作就是晶体测量，或称晶体测角。晶体测量使用的仪器有接触测角仪和反射测角仪。一、接触测角仪接触测角仪结构简单，主要由两部分组成（图3-3）：1.半圆仪：上有0°-180°的刻度：2.直臂：固定在半圆仪的中心，可以自由旋转。测量晶体时，把半圆仪的底边和直臂与欲测的两个晶面靠紧，并使此二晶面相交的晶棱与测角仪的平面垂直，此时即可在半圆仪上读得晶面的面角数据。此种仪器使用简便，但精度较差（误差0.5°1°），且不适于测量小晶体。二、反射测角仪1.单圈反射测角仪结构如图3-4所示，M为一周边有刻度的水平圆盘，可以绕轴旋转：V为游标：K为平行光管：F为视物管，K和F的轴线均与圆盘轴线垂直，且三者交圆盘中心于一点。（1）原理与方法：单圈反射测角仪的基本原理是利用光的反射定律，即光的入射角等于反射角。测量方法如下：①用胶蜡把晶体固定在圆盘中心，并使欲测二晶面的交棱与圆盘旋转轴平行：②打开光源，使光线通过视物管平行射向晶面a：③转动圆盘，使晶面a的法线恰好为光管K和视物管F的分角线，此时，从视物管可以看到由a反射的光线，记下刻度盘读数：26

26 的外形自然也不一样， 但是对应晶面间的夹角完全相等。 面角恒等是格子构造的必然结果。因为同种 晶体具有完全相同的格子构造，格子构造中 的同种面网构成晶体外形上的同种晶面。晶 体生长过程中，晶面平行向外推移，故不论 晶面大小形态如何，对应晶面间的夹角恒定 不变。 面角恒等定律的发现，对结晶学的发展 有深远的影响，使人类从千变万化的实际晶 体中找出了同种晶体外形上的固有规律，并 用面角测量和投影的方法，恢复晶体的理想 图 3-2 晶面夹角和面角 形态，奠定了几何结晶学的基础。 第二节 晶体测量 由面角恒等定律可知，只要知道了各晶面间的面角关系，就有可能恢复晶体的 理想几何外形。为此，需要实际测量晶面之间的夹角，以获得面角数据。这项工作 就是晶体测量，或称晶体测角。 晶体测量使用的仪器有接触测角仪和反射测角仪。 一、接触测角仪 接触测角仪结构简单，主要由两部分组成（图 3-3）： ⒈ 半圆仪：上有 0°-180°的刻度； ⒉ 直臂：固定在半圆仪的中心，可以自由旋转。 测量晶体时，把半圆仪的底边和直臂与欲测的两个晶面靠紧，并使此二晶面相 交的晶棱与测角仪的平面垂直，此时即可在半圆仪上读得晶面的面角数据。此种仪 器使用简便，但精度较差（误差 0.5°-1°），且不适于测量小晶体。 二、 反射测角仪 ⒈ 单圈反射测角仪 结构如图 3-4 所示，M 为一周边有刻度的水平圆盘，可以绕轴旋转；V 为游标； K 为平行光管；F 为视物管，K 和 F 的轴线均与圆盘轴线垂直，且三者交圆盘中心于 一点。 ⑴ 原理与方法：单圈反射测角仪的基本原理是利用光的反射定律，即光的入射 角等于反射角。测量方法如下： ① 用胶蜡把晶体固定在圆盘中心，并使欲测二晶面的交棱与圆盘旋转轴平行； ② 打开光源，使光线通过视物管平行射向晶面 a； ③ 转动圆盘，使晶面 a 的法线恰好为光管 K 和视物管 F 的分角线，此时，从视 物管可以看到由 a 反射的光线，记下刻度盘读数；

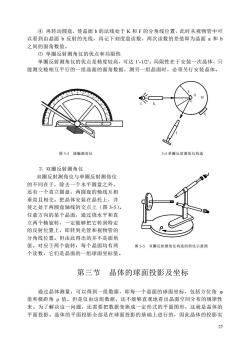
④再转动圆盘，使晶面b的法线处于K和F的分角线位置，此时从视物管中可以看到由晶面b反射的光线，再记下刻度盘读数，两次读数的差值即为晶面a和b之间的面角数值。(2）单圈反射测角仪的优点和局限性单圈反射测角仪的优点是精度较高，可达1-1/2；局限性在于安装一次晶体，只能测交棱相互平行的一组晶面的面角数据，测另一组晶面时，必须另行安装晶体。图3-3接触测角仪3-4单圈反射测角仪构造2.双圈反射测角仪双圈反射测角仪与单圈反射测角仪的不同在于，除去一个水平圆盘之外，还有一个直立圆盘，两圆盘的轴线互相垂直且相交。把晶体安装在晶托上，并使之处于两圆盘轴线的交点上（图3-5）。任意方向的某个晶面，通过绕水平和直立两个轴旋转，一定能够把它转到特定的反射位置上，即转到光管和视物管的分角线位置。但由此得出的并不是面角值。对应于两个旋转，每个晶面均有两图3-5双圈反射测角仪构造的简化示意图个读数，它们是晶面的一组球面坐标值。第三节晶体的球面投影及坐标通过晶体测量，可以得到一组数据，即每一个晶面的球面坐标，包括方位角值和极距角P值。但是仅由这组数据，还不能够直观地看出晶面空间分布的规律性来。为了解决这一问题，还需要把数据变换成一定形式的平面图形，这就是晶体的平面投影。晶体的平面投影全部是在球面投影的基础上进行的，因此晶体的投影实27

27 ④ 再转动圆盘，使晶面 b 的法线处于 K 和 F 的分角线位置，此时从视物管中可 以看到由晶面 b 反射的光线，再记下刻度盘读数，两次读数的差值即为晶面 a 和 b 之间的面角数值。 ⑵ 单圈反射测角仪的优点和局限性 单圈反射测角仪的优点是精度较高，可达 1′-1/2′；局限性在于安装一次晶体，只 能测交棱相互平行的一组晶面的面角数据，测另一组晶面时，必须另行安装晶体。 图 3-3 接触测角仪 3-4 单圈反射测角仪构造 ⒉ 双圈反射测角仪 双圈反射测角仪与单圈反射测角仪 的不同在于，除去一个水平圆盘之外， 还有一个直立圆盘，两圆盘的轴线互相 垂直且相交。把晶体安装在晶托上，并 使之处于两圆盘轴线的交点上（图 3-5）。 任意方向的某个晶面，通过绕水平和直 立两个轴旋转，一定能够把它转到特定 的反射位置上，即转到光管和视物管的 分角线位置。但由此得出的并不是面角 值。对应于两个旋转，每个晶面均有两 图 3-5 双圈反射测角仪构造的简化示意图 个读数，它们是晶面的一组球面坐标值。 第三节 晶体的球面投影及坐标 通过晶体测量，可以得到一组数据，即每一个晶面的球面坐标，包括方位角 φ 值和极距角 ρ 值。但是仅由这组数据，还不能够直观地看出晶面空间分布的规律性 来。为了解决这一问题，还需要把数据变换成一定形式的平面图形，这就是晶体的 平面投影。晶体的平面投影全部是在球面投影的基础上进行的，因此晶体的投影实

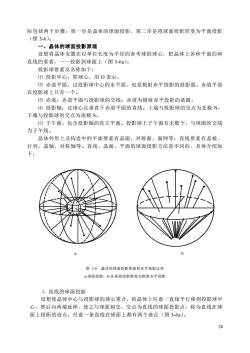
际包括两个步骤：第一步是晶体的球面投影，第二步是将球面投影转变为平面投影(图3-6)。一、晶体的球面投影原理设想将晶体安置在以单位长度为半径的参考球的球心，把晶体上各种平面的和直线的要素，一一投影到球面上（图3-6a）。投影球要素及名称如下：（1）投影中心：即球心，用O表示。(2）赤道平面：过投影球中心的水平面，也是极射赤平投影的投影面。赤道平面在投影球上只有一个。(3）赤道：赤道平面与投影球的交线：赤道为极射赤平投影的基圆。（4）投影轴：过球心且垂直于赤道平面的直线。上端与投影球的交点为北极N，下端与投影球的交点为南极S。(5）子午面：包含投影轴的直立平面。投影球上子午面有无数个，与球面的交线为子午线。晶体外形上及构造中的平面要素有晶面、对称面、面网等：直线要素有晶棱、行列、晶轴、对称轴等。直线、晶面、平面的球面投影方法是不同的，具体介绍如下:ba图3-6品体的球面投影和极射平投影过程a-球面投影：b-从球面投影转变为极射赤平投影1.直线的球面投影设想使晶体中心与投影球的球心重合，将晶体上任意一直线平行移到投影球中心，然后向两端延伸，使之与球面相交，交点为直线的球面投影点，称为直线在球面上投影的迹点。任意一条直线在球面上都有两个迹点（图3-6a）。28

28 际包括两个步骤：第一步是晶体的球面投影，第二步是将球面投影转变为平面投影 （图 3-6）。 一、晶体的球面投影原理 设想将晶体安置在以单位长度为半径的参考球的球心，把晶体上各种平面的和 直线的要素，一一投影到球面上（图 3-6a）。 投影球要素及名称如下： ⑴ 投影中心：即球心，用 O 表示。 ⑵ 赤道平面：过投影球中心的水平面，也是极射赤平投影的投影面。赤道平面 在投影球上只有一个。 ⑶ 赤道：赤道平面与投影球的交线；赤道为极射赤平投影的基圆。 ⑷ 投影轴：过球心且垂直于赤道平面的直线。上端与投影球的交点为北极 N， 下端与投影球的交点为南极 S。 ⑸ 子午面：包含投影轴的直立平面。投影球上子午面有无数个，与球面的交线 为子午线。 晶体外形上及构造中的平面要素有晶面、对称面、面网等；直线要素有晶棱、 行列、晶轴、对称轴等。直线、晶面、平面的球面投影方法是不同的，具体介绍如 下： a b 图 3-6 晶体的球面投影和极射赤平投影过程 a-球面投影；b-从球面投影转变为极射赤平投影 ⒈ 直线的球面投影 设想使晶体中心与投影球的球心重合，将晶体上任意一直线平行移到投影球中 心，然后向两端延伸，使之与球面相交，交点为直线的球面投影点，称为直线在球 面上投影的迹点。任意一条直线在球面上都有两个迹点（图 3-6a）

可以看出，所有直线都必须平移到投影球中心，然后才能进行投影。因此所有方向相同的直线，在球面上的投影点的方位都相同。直线的球面投影点只能反映直线的方向，而不能反映直线的具体位置。2.晶面的球面投影(1）投影方法设想将晶体中心与投影球中心重合，过中心作某晶面的法线，并延伸使之与球面相交，交点就是该晶面的球面投影点，称为该晶面的极点，如图3-6a和3-7所示，在图3-8中，a点为晶面A的球面投影点，即晶面A的极点。任意一晶面在球面上的投影均为一个点。晶面的球面投影点只能反映晶面的空间方位，与晶面的实际形态和大小无关。NNS图3-7品品体上品面的球面投影极点图3-8球面上投影点的极射赤平投影(2）球面上投影点的坐标（极距角和方位角）地球上任意一点的位置都可以用经度和纬度来表示。如果像地球上的经纬线那样，在投影球面上画上坐标网线的话，那么，投影点在球面上的位置，也可以用该点的极距角和方位角这两个球面坐标来表示。在球面坐标网中，与纬度相当的是极距角P，与经度相当的是方位角。如图3-8和3-9所示。①极距角（p）：投影轴与晶面法线或直线间的夹角，也就是北极N与球面上投影点之间的弧度，故称极距角。极距角都是从北极N点开始度量，从投影球N极到S极，共分180°②方位角（β）：是包含晶面法线或直线要素的子午面与投影球零子午面之间的夹角。也就是球面上投影点所在的子午线与零子午线之间的水平弧度，故称方位角。方位角都是从零度子午线（=0°，一般在投影球最右侧）开始顺时针方向计角的，投影球一周的方位角共分为360。显然，有了球面坐标网以后，只要知道投影点的球面坐标值，即可以确定投影点在球面上的位置。29

29 可以看出，所有直线都必须平移到投影球中心，然后才能进行投影。因此所有 方向相同的直线，在球面上的投影点的方位都相同。直线的球面投影点只能反映直 线的方向，而不能反映直线的具体位置。 ⒉ 晶面的球面投影 ⑴ 投影方法 设想将晶体中心与投影球中心重合，过中心作某晶面的法线，并延伸使之与球 面相交，交点就是该晶面的球面投影点，称为该晶面的极点，如图 3-6a 和 3-7 所示， 在图 3-8 中，a 点为晶面 A 的球面投影点，即晶面 A 的极点。 任意一晶面在球面上的投影均为一个点。晶面的球面投影点只能反映晶面的空 间方位，与晶面的实际形态和大小无关。 图 3-7 晶体上晶面的球面投影极点 图 3-8 球面上投影点的极射赤平投影 ⑵ 球面上投影点的坐标（极距角和方位角） 地球上任意一点的位置都可以用经度和纬度来表示。如果像地球上的经纬线那 样，在投影球面上画上坐标网线的话，那么，投影点在球面上的位置，也可以用该 点的极距角和方位角这两个球面坐标来表示。 在球面坐标网中，与纬度相当的是极距角 ρ，与经度相当的是方位角 φ。如图 3-8 和 3-9 所示。 ① 极距角（ρ）：投影轴与晶面法线或直线间的夹角，也就是北极 N 与球面上 投影点之间的弧度，故称极距角。极距角都是从北极 N 点开始度量，从投影球 N 极 到 S 极，共分 180°。 ② 方位角（）：是包含晶面法线或直线要素的子午面与投影球零子午面之间 的夹角。也就是球面上投影点所在的子午线与零子午线之间的水平弧度，故称方位 角。方位角都是从零度子午线（=0°，一般在投影球最右侧）开始顺时针方向计角 的，投影球一周的方位角共分为 360°。 显然，有了球面坐标网以后，只要知道投影点的球面坐标值，即可以确定投影 点在球面上的位置

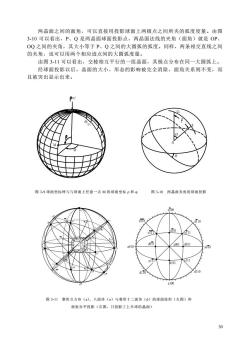
两晶面之间的面角，可以直接用投影球面上两极点之间所夹的弧度度量。由图3-10可以看出，P、Q是两晶面球面投影点，两晶面法线的夹角（面角）就是OP、OQ之间的夹角，其大小等于P、Q之间的大圆弧的弧度。同样，两条相交直线之间的夹角，也可以用两个相应迹点间的大圆弧度量。由图3-11可以看出，交棱相互平行的一组晶面，其极点分布在同一大圆弧上。经球面投影以后，晶面的大小、形态的影响被完全消除，面角关系则不变，而且被突出显示出来。P-0*图3-9球面坐标网与与球面上任意一点M的球面坐标p和图3-10两品面夹角的球面投影aToodTTOdT10dTolOTTIT1IdOTIdo1100a010aOTOoITPollld101d110diToXa100图3-11聚形立方体（a）、八面体（o）与菱形十二面体（d）的球面投形（左图）和极射赤平投影（右图，只投影了上半球的晶面）30

30 两晶面之间的面角，可以直接用投影球面上两极点之间所夹的弧度度量。由图 3-10 可以看出，P、Q 是两晶面球面投影点，两晶面法线的夹角（面角）就是 OP、 OQ 之间的夹角，其大小等于 P、Q 之间的大圆弧的弧度。同样，两条相交直线之间 的夹角，也可以用两个相应迹点间的大圆弧度量。 由图 3-11 可以看出，交棱相互平行的一组晶面，其极点分布在同一大圆弧上。 经球面投影以后，晶面的大小、形态的影响被完全消除，面角关系则不变，而 且被突出显示出来。 图 3-9 球面坐标网与与球面上任意一点 M 的球面坐标 ρ 和 φ 图 3-10 两晶面夹角的球面投影 图 3-11 聚形立方体（a）、八面体（o）与菱形十二面体（d）的球面投形（左图）和 极射赤平投影（右图，只投影了上半球的晶面）

3.平面的球面投影除晶面以外的平面（如对称面），球面投影的方法与晶面不同。投影时设想将晶体中心与投影球中心重合，将平面扩展后与投影球相交，平面与投影球的交线就是该平面的球面投影。晶体上任一平面的球面投影均为圆。通过投影中心的平面，其球面投影是一个与投影球等径同心的圆，称大圆：不通过投影中心的平面，其球面投影均小于大圆，称为小圆。球面投影可以真实地表示晶体上各种要系的空间儿何关系。由于这只是一种空间关系，在实际的研究工作中难以应用，只有将它们投影到平面上，成为平面的投影图形，才有实用价值。将球面投影转变为平面投影的方法有正投影、极射赤平投影和心射赤平投影。下面介绍应用广泛的极射赤平投影。第四节极射赤平投影晶体的平面投影都是以球面投影为基础的。也就是说，在对晶体进行投影时，先进行球面投影，再进行平面投影，极射赤平投影也是如此。极射赤平投影以投影球的赤道平面作为投影面，以南极或北极为视点，所以称极射赤平投影。投影面与投影球的交线（投影球赤道）称为基圆。一、晶面的极射赤平投影1.投影方法上一节已经介绍，任一晶面在球面上的投影是一个点。晶面的极射赤平投影就是把晶面在球面上的投影点与南极（或北极）连线，连线交赤道平面于一点，该交点就是晶面的极射赤平投影点。如图3-8所示，图中晶面的球面投影极点为A，极射赤平投影点为a。2.极射赤平投影点的坐标极射赤平投影点在投影平面上的坐标也是用极距角和方位角表示的，在图3-8中，a点的极距角等于o与a之间的直线长度所代表的弧度。oa=rtgp/2(r为基圆半径)。3.晶面的极射赤平投影点在投影平面（基圆）上的位置水平晶面的极射赤平投影点落在基圆中心：直立晶面的极射赤平投影点落在基圆上：倾斜晶面的极射赤平投影点落在基圆内，且倾斜角度越大投影点越接近于基圆。4.晶面的极射赤平投影点的表示方法晶面的球面投影点在北半球，以南极为视点进行投影，投影点用“。表示：晶面的球面投影点在南半球，以北极为视点进行投影，投影点用“o”表示。二、平面的极射赤平投影31

31 ⒊ 平面的球面投影 除晶面以外的平面（如对称面），球面投影的方法与晶面不同。 投影时设想将晶体中心与投影球中心重合，将平面扩展后与投影球相交，平面 与投影球的交线就是该平面的球面投影。晶体上任一平面的球面投影均为圆。通过 投影中心的平面，其球面投影是一个与投影球等径同心的圆，称大圆；不通过投影 中心的平面，其球面投影均小于大圆，称为小圆。 球面投影可以真实地表示晶体上各种要素的空间几何关系。由于这只是一种空 间关系，在实际的研究工作中难以应用，只有将它们投影到平面上，成为平面的投 影图形，才有实用价值。 将球面投影转变为平面投影的方法有正投影、极射赤平投影和心射赤平投影。 下面介绍应用广泛的极射赤平投影。 第四节 极射赤平投影 晶体的平面投影都是以球面投影为基础的。也就是说，在对晶体进行投影时， 先进行球面投影，再进行平面投影，极射赤平投影也是如此。 极射赤平投影以投影球的赤道平面作为投影面，以南极或北极为视点，所以称 极射赤平投影。投影面与投影球的交线（投影球赤道）称为基圆。 一、晶面的极射赤平投影 ⒈ 投影方法 上一节已经介绍，任一晶面在球面上的投影是一个点。晶面的极射赤平投影就 是把晶面在球面上的投影点与南极（或北极）连线，连线交赤道平面于一点，该交 点就是晶面的极射赤平投影点。如图 3-8 所示，图中晶面的球面投影极点为 A，极射 赤平投影点为 a。 ⒉ 极射赤平投影点的坐标 极射赤平投影点在投影平面上的坐标也是用极距角和方位角表示的，在图 3-8 中，a 点的极距角等于 o 与 a 之间的直线长度所代表的弧度。 oa = rtg/2 (r 为基圆半径)。 ⒊ 晶面的极射赤平投影点在投影平面（基圆）上的位置 水平晶面的极射赤平投影点落在基圆中心；直立晶面的极射赤平投影点落在基 圆上；倾斜晶面的极射赤平投影点落在基圆内，且倾斜角度越大投影点越接近于基 圆。 ⒋ 晶面的极射赤平投影点的表示方法 晶面的球面投影点在北半球，以南极为视点进行投影，投影点用“”表示；晶面 的球面投影点在南半球，以北极为视点进行投影，投影点用“○”表示。 二、平面的极射赤平投影

晶体上平面的球面投影均为圆，极射赤平投影仍以S极（或N极）为视点，将球面上的圆形迹线与S极（或N极）连线，连线与投影平面的交线就是平面的极射赤平投影。1.通过投影中心的平面，其球面投影是一个与投影球等径同心的大圆，极射赤平投影有三种情况：(1）水平大圆的极射赤平投影就是基圆（图3-12)：(2）直立大圆的极射赤平投影为基圆直径（图3-12)；(3）倾斜大圆的极射赤平投影为以基圆直径为弦的大圆弧（图3-13）。除水平大圆之外，投影球上所有大圆都被投影平面分为上下两部分，作图时一般以南极为视点，只对上半个大圆进行极射赤平投影。2.不通过投影中心的平面，球面投影都是小圆，其极射赤平投影也有三种情况：（1）与投影平面平行的小圆，极射赤平投影仍为小圆，且与基圆同心。离投影平面越近，小圆越大，越远，小圆越小（图3-14）。(2）与投影平面垂直的直立小圆，极射赤平投影为一小圆弧，小圆弧的弦是小圆与基圆两个交点的连线（图3-15）。CRSSO图3-12直立、水平大圆的极射赤平投影图3-13倾斜大圆的极射赤平投影NNs图3-14球面上水平小圆图3-15球面上直立小圆图3-16球面上任意倾斜的小圆的极射赤平投影的极射赤平投影的极射赤平投影32

32 晶体上平面的球面投影均为圆，极射赤平投影仍以 S 极（或 N 极）为视点，将 球面上的圆形迹线与 S 极（或 N 极）连线，连线与投影平面的交线就是平面的极射 赤平投影。 ⒈ 通过投影中心的平面，其球面投影是一个与投影球等径同心的大圆，极射赤 平投影有三种情况： ⑴ 水平大圆的极射赤平投影就是基圆（图 3-12）； ⑵ 直立大圆的极射赤平投影为基圆直径（图 3-12）； ⑶ 倾斜大圆的极射赤平投影为以基圆直径为弦的大圆弧（图 3-13）。 除水平大圆之外，投影球上所有大圆都被投影平面分为上下两部分，作图时一 般以南极为视点，只对上半个大圆进行极射赤平投影。 ⒉ 不通过投影中心的平面，球面投影都是小圆，其极射赤平投影也有三种情况： ⑴ 与投影平面平行的小圆，极射赤平投影仍为小圆，且与基圆同心。离投影平 面越近，小圆越大，越远，小圆越小（图 3-14）。 ⑵ 与投影平面垂直的直立小圆，极射赤平投影为一小圆弧，小圆弧的弦是小圆 与基圆两个交点的连线（图 3-15）。 图 3-12 直立、水平大圆的极射赤平投影 图 3-13 倾斜大圆的极射赤平投影 图 3-14 球面上水平小圆 图 3-15 球面上直立小圆 图 3-16 球面上任意倾斜的小圆 的极射赤平投影 的极射赤平投影 的极射赤平投影

(3）与投影面斜交的倾斜小圆，极赤投影仍为小圆，但圆心与基圆中心不重合。（图3-16）综上所述，归纳如下：①投影球面上圆形迹线的极射赤平投影可以是大圆或小圆，大圆弧或小圆弧也可以是直线。②极射赤平投影面上两点间的角度等于球面上相应两点间的角度。③极射赤平投影面上两大圆弧之间的夹角等于球面上两大圆之间的夹角。可见，极射赤平投影保留了球面上的各种角度关系，这给作图和研究晶体的各种几何规律常带来极大方便。第五节吴氏网在上面几节中，我们从原理上叙述了晶体进行极射赤平投影的全过程。但是在实际工作中，并不是先作球面投影，然后再转换成极射赤平投影的。而是将球面上的坐标网线也进行极射赤平投影，得到一张平面的坐标网。利用平面坐标网，根据每一个晶面的球面坐标值，可以直接在坐标网上标定各个投影点的位置。这种利用极射赤平投影原理绘制的坐标网就是昊氏网。一、吴氏网的构成（图3-17）(1）网面：相当于极射赤平投影面。（2）基圆：极射赤平投影面与投影球面相交的水平大圆。(3）目测点（投影球的南极或北极）：位于网面中心。（4）直径：两个垂直投影面且互相垂直的大圆投影。（5）大圆弧：包含投影球的同一直径，倾斜角度各不相同的一组倾斜大圆的投影。（6）小圆弧：与投影面垂直且相互垂平行的一组直立小圆的投影。二、吴氏网用途标准的吴氏网，其基圆直径为20cm；网线的分度为每格2°。但是在两极附近经线的间隔为10°。作图时的精度一般要求达到0.5°：没有落在网线上的点，其网线间的分度可以用插入法估计确定。吴氏网的用途很广。在结晶学中，吴氏网可作为球面坐标的量角规。在基圆上可以度量方位角β：直径上的刻度可以度量极距角p：大圆弧上的刻度可以度量两晶面或两平面之间的夹角：可根据投影图进行图解计算晶体常数、确定晶面符号等。此外，吴氏网在晶体光学、岩石学、航空航天学、航海学、天文测量学、晶体X射线学、电子显微学等方面均有广泛的应用。三、昊氏网的应用举例在应用昊氏网进行投影时，需要透明纸、大头针、铅笔等作图工具。投影方法步骤如下：33

33 ⑶ 与投影面斜交的倾斜小圆，极赤投影仍为小圆，但圆心与基圆中心不重合。 （图 3-16） 综上所述，归纳如下： ① 投影球面上圆形迹线的极射赤平投影可以是大圆或小圆，大圆弧或小圆弧， 也可以是直线。 ② 极射赤平投影面上两点间的角度等于球面上相应两点间的角度。 ③ 极射赤平投影面上两大圆弧之间的夹角等于球面上两大圆之间的夹角。 可见，极射赤平投影保留了球面上的各种角度关系，这给作图和研究晶体的各 种几何规律常带来极大方便。 第五节 吴氏网 在上面几节中，我们从原理上叙述了晶体进行极射赤平投影的全过程。但是在 实际工作中，并不是先作球面投影，然后再转换成极射赤平投影的。而是将球面上 的坐标网线也进行极射赤平投影，得到一张平面的坐标网。利用平面坐标网，根据 每一个晶面的球面坐标值，可以直接在坐标网上标定各个投影点的位置。这种利用 极射赤平投影原理绘制的坐标网就是吴氏网。 一、吴氏网的构成（图 3-17） ⑴ 网面：相当于极射赤平投影面。 ⑵ 基圆：极射赤平投影面与投影球面相交的水平大圆。 ⑶ 目测点（投影球的南极或北极）：位于网面中心。 ⑷ 直径：两个垂直投影面且互相垂直的大圆投影。 ⑸ 大圆弧：包含投影球的同一直径，倾斜角度各不相同的一组倾斜大圆的投影。 ⑹ 小圆弧：与投影面垂直且相互垂平行的一组直立小圆的投影。 二、吴氏网用途 标准的吴氏网，其基圆直径为 20cm；网线的分度为每格 2°。但是在两极附近， 经线的间隔为 10°。作图时的精度一般要求达到 0.5°；没有落在网线上的点，其网线 间的分度可以用插入法估计确定。 吴氏网的用途很广。在结晶学中，吴氏网可作为球面坐标的量角规。在基圆上 可以度量方位角；直径上的刻度可以度量极距角；大圆弧上的刻度可以度量两晶 面或两平面之间的夹角；可根据投影图进行图解计算晶体常数、确定晶面符号等。 此外，吴氏网在晶体光学、岩石学、航空航天学、航海学、天文测量学、晶体 X 射线学、电子显微学等方面均有广泛的应用。 三、吴氏网的应用举例 在应用吴氏网进行投影时，需要透明纸、大头针、铅笔等作图工具。投影方法 步骤如下：

图3-17吴氏网（1）将透明纸覆于网面上，用大头针在网心将两者固定在一起，使透明纸能够相对于吴氏网旋转。(2）用铅笔在透明纸上描出基圆，并用“×”表出网心。（3）在基圆上选一点（一般在直径右侧端点）作为0=0°的标志。(4）此时若已知某一晶面M的球面坐标值为p=66°，=120°，我们就可以从透明纸上的=0°开始，顺时针沿基圆数120°，此时这一点若与基圆中心连线的话，则此半径必为=120°的等值线，晶面M的投影点必位于此半径上。然后，转动透明纸，使β=120°的点与基圆任一直径端点重合，从中心沿此直径向端点方向数66°，得到一点，此点就是M的投影点位置（图3-18）。34

34 图 3-17 吴氏网 ⑴ 将透明纸覆于网面上，用大头针在网心将两者固定在一起，使透明纸能够相 对于吴氏网旋转。 ⑵ 用铅笔在透明纸上描出基圆，并用 “×”表出网心。 ⑶ 在基圆上选一点（一般在直径右侧端点）作为=0°的标志。 ⑷ 此时若已知某一晶面 M 的球面坐标值为 ρ=66°，=120°，我们就可以从透明 纸上的=0o 开始，顺时针沿基圆数 120°，此时这一点若与基圆中心连线的话，则此 半径必为=120°的等值线，晶面 M 的投影点必位于此半径上。然后，转动透明纸， 使=120°的点与基圆任一直径端点重合，从中心沿此直径向端点方向数 66°，得到一 点，此点就是 M 的投影点位置（图 3-18）