大连理工大学：《数据结构》课程教学课件（PPT讲稿）第五章 树

第五章树 树是一类重要的非线性数据结构，是以分支关 系定义的层次结构 §5.1树的定义 ★定义 定义：树(tree)是n(n>O)个结点的有限集T,其中： ●有且仅有一个特定的结点，称为树的根(【00) ●当n>1时，其余结点可分为m(m>0)个互不相交的有限集 T1,T2,.Tm,其中每一个集合本身又是一棵树，称为根的 子树(subtree) 必特点： ●树中至少有一个结点—根 ●树中各子树是互不相交的集合

第五章 树 树是一类重要的非线性数据结构，是以分支关 系定义的层次结构 §5.1 树的定义 定义 ❖定义：树(tree)是n(n>0)个结点的有限集T，其中： ⚫有且仅有一个特定的结点，称为树的根(root) ⚫当n>1时，其余结点可分为m(m>0)个互不相交的有限集 T1,T2,.Tm，其中每一个集合本身又是一棵树，称为根的 子树(subtree) ❖特点： ⚫树中至少有一个结点——根 ⚫树中各子树是互不相交的集合

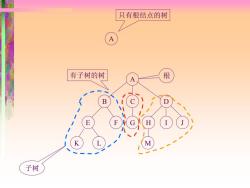
只有根结点的树 有子树的树 根 子树

A 只有根结点的树 A B C D E F G H I J K L M 有子树的树 根 子树

★基本术语 结点(n0d)一表示树中的元素，包括数据项及若干 指向其子树的分支 结点的度(degree) 一结点拥有的子树数 叶子(leaf)一度为0的结点 冬孩子(child一结点子树的根称为该结点的孩子 双亲(parents)—孩子结点的上层结点叫该结点的~ 冬兄弟(sibling)一J同一双亲的孩子 必树的度 棵树中最大的结点度数 冬结点的层次(level)一从根结点算起， 根为第一层， 它的孩子为第二层 必深度(depth)—树中结点的最大层次数 森林(forest)—m(m≥0)棵互不相交的树的集合

基本术语 ❖结点(node)——表示树中的元素，包括数据项及若干 指向其子树的分支 ❖结点的度(degree)——结点拥有的子树数 ❖叶子(leaf)——度为0的结点 ❖孩子(child)——结点子树的根称为该结点的孩子 ❖双亲(parents)——孩子结点的上层结点叫该结点的~ ❖兄弟(sibling)——同一双亲的孩子 ❖树的度——一棵树中最大的结点度数 ❖结点的层次(level)——从根结点算起，根为第一层， 它的孩子为第二层. ❖深度(depth)——树中结点的最大层次数 ❖森林(forest)——m(m0)棵互不相交的树的集合

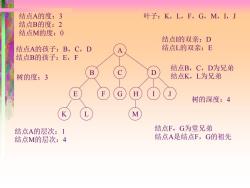
结点A的度：3 叶子：K,L,F,G,M,I,J 结点B的度：2 结点M的度：O 结点I的双亲：D 结点A的孩子：B,C,D 结点L的双亲：E 结点B的孩子：E,F 结点B,C,D为兄弟 B 树的度：3 结点K,L为兄弟 E 树的深度：4 结点A的层次：1 结点F,G为堂兄弟 结点M的层次：4 结点A是结点F,G的祖先

A B C D E F G H I J K L M 结点A的度：3 结点B的度：2 结点M的度：0 叶子：K，L，F，G，M，I，J 结点A的孩子：B，C，D 结点B的孩子：E，F 结点I的双亲：D 结点L的双亲：E 结点B，C，D为兄弟 树的度：3 结点K，L为兄弟 结点A的层次：1 结点M的层次：4 树的深度：4 结点F，G为堂兄弟 结点A是结点F，G的祖先

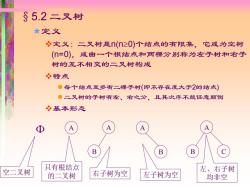
§5.2二叉树 ★定义 冬定义：二叉树是n(≥0)个结点的有限集，它或为空树 (=0),或由一个根结点和两棵分别称为左子树和右子 树的互不相交的二叉树构成 冬特点 ●每个结点至多有二棵子树（即不存在度大于2的结点） ●二叉树的子树有左、右之分，且其次序不能任意颠倒 基本形态 A B B 空二叉树 只有根结点 左、右子树 的二叉树 右子树为空 左子树为空 均非空

§5.2 二叉树 定义 ❖定义：二叉树是n(n0)个结点的有限集，它或为空树 (n=0)，或由一个根结点和两棵分别称为左子树和右子 树的互不相交的二叉树构成 ❖特点 ⚫每个结点至多有二棵子树(即不存在度大于2的结点) ⚫二叉树的子树有左、右之分，且其次序不能任意颠倒 ❖基本形态 A 只有根结点 的二叉树  空二叉树 A B 右子树为空 A B 左子树为空 A B C 左、右子树 均非空

★二叉树性质 性质1：在二叉树的第层上至多有2个结点(i≥1) 证明：用归纳法证明之 ①=1时，只有一个根结点2-1=2°=1是对的 ②假设对所有j(1≤j<)命题成立，即第j层上至多有21个结点 那么，第i-1层至多有2-2个结点 又二叉树每个结点的度至多为2 .第层上最大结点数是第i-1层的2倍，即2·2-2=21 故命题得证 冬性质2：深度为k的二叉树至多有2-1个结点(k≥1) 证明：由性质1，可得深度为k的二叉树最大结点数是 ∑（第层的最大结点数）=∑2=2-1

二叉树性质 ❖性质1： 2 ( 1) 1  − i i 在二叉树的第 层上至多有 i 个结点 证明：用归纳法证明之 i=1时，只有一个根结点， 是对的 假设对所有j(1j<i)命题成立，即第j层上至多有 个结点 那么，第i-1层至多有 个结点 又二叉树每个结点的度至多为2  第i层上最大结点数是第i-1层的2倍，即 故命题得证 2 2 1 1 0 = = i− 1 2 j− 2 2 i− 2 1 2 2 2 − −  = i i ❖性质2：深度为k的二叉树至多有 2 −1 个结点(k1) k 证明：由性质1，可得深度为k 的二叉树最大结点数是 ( ) 2 2 1 1 1 1  =  = − = = − k k i k i i 第i层的最大结点数

性质3：对任何一棵二叉树T,如果其终端结点数为0， 度为2的结点数为n2,则no=n2+1 证明：n1为二叉树T中度为1的结点数 因为：二叉树中所有结点的度均小于或等于2 所以：其结点总数n=no+n1+n2 又二叉树中，除根结点外，其余结点都只有一个 分支进入 设B为分支总数，则n=B+1 又：分支由度为1和度为2的结点射出，∴.B=ni+2n2 于是，n=B+1=n1+2n2+l=n0+n1+n2 ∴.n0=n2+1

❖性质3：对任何一棵二叉树T，如果其终端结点数为n0， 度为2的结点数为n2，则n0=n2+1 证明：n1为二叉树T中度为1的结点数 因为：二叉树中所有结点的度均小于或等于2 所以：其结点总数n=n0+n1+n2 又二叉树中，除根结点外，其余结点都只有一个 分支进入 设B为分支总数，则n=B+1 又：分支由度为1和度为2的结点射出，B=n1+2n2 于是，n=B+1=n1+2n2+1=n0+n1+n2 n0=n2+1

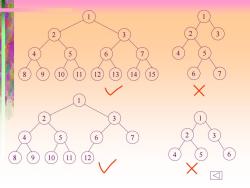
★几种特殊形式的二叉树 满二叉树 ●定义：一棵深度为k且有2-1个结点的二叉树称为、 ●特点：每一层上的结点数都是最大结点数 完全二叉树 ●定义：深度为k,有个结点的二叉树当且仅当其每一个结点 都与深度为k的满二叉树中编号从1至的结点一一对应时， 称为~ ●特点 ◆叶子结点只可能在层次最大的两层上出现 ◆对任一结点，若其右分支下子孙的最大层次为引，则其左 分支下子孙的最大层次必为1或+1 ●性质 ◆性质4：具有n个结点的完全二叉树的深度为log2n+1 D

几种特殊形式的二叉树 ❖满二叉树 ⚫定义： 一棵深度为 且有2 −1个结点的二叉树称为~ k k ⚫特点：每一层上的结点数都是最大结点数 ❖完全二叉树 ⚫定义：深度为k，有n个结点的二叉树当且仅当其每一个结点 都与深度为k的满二叉树中编号从1至n的结点一一对应时， 称为~ ⚫特点 ◆叶子结点只可能在层次最大的两层上出现 ◆对任一结点，若其右分支下子孙的最大层次为l，则其左 分支下子孙的最大层次必为l 或l+1 ⚫性质 ◆性质4： 具有n个结点的完全二叉树的深度为log 2 n +1

2 3 3 6 5 8 6 X 2 3 4 5 2 6 3 8 10 1 12 5 6

1 2 3 11 4 5 8 9 12 13 6 7 10 14 15 1 2 3 11 4 5 8 9 12 6 7 10 1 2 3 4 5 6 7 1 2 3 4 5 6

◆性质5：如果对一棵有个结点的完全二叉树的结点按层序编号， 则对任一结点i(1≤≤n),有： (1)如果i1,则结点i是二又树的根，无双亲；如果>1，则其 双亲是i/2] (2)如果2i>n,则结点i无左孩子；如果2i≤n,则其左孩子是2i (3)如果2i+1>n,则结点i无右孩子；如果2i+1≤n,则其右孩子 是2i+1

◆性质5：如果对一棵有n个结点的完全二叉树的结点按层序编号， 则对任一结点i(1in)，有： (1) 如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其 双亲是i/2 (2) 如果2i>n，则结点i无左孩子；如果2in，则其左孩子是2i (3) 如果2i+1>n，则结点i无右孩子；如果2i+1n，则其右孩子 是2i+1