《数据结构》课程教学资源（教材讲义）二叉树网上资料

第六章二叉树 在前面几章里讨论的数据结构都属于线性结构，线性结构的特点是逻辑结构简单，易 于进行查找、插入和删除等操作，其主要用于对客观世界中具有单一的前驱和后继的数据 关系进行描述，而现实中的许多事物的关系并非这样简单，如人类社会的族谱、各种社会 组织机构以及城市交通、通讯等，这些事物中的联系都是非线性的，采用非线性结构进行 描绘会更明确和便利。 所谓非线性结构是指，在该结构中至少存在一个数据元素，有两个或两个以上的直接 前驱（或直接后继）元素。树型结构和图型就是其中十分重要的非线性结构，可以用来描 述客观世界中广泛存在的层次结构和网状结构的关系，如前面提到的族谱、城市交通等。 在本书的第六、七、八章将重点讨论这两类非线性结构的有关概念、存储结构、在各种存 储结构上所实施的一些运算以及有关的应用实例。 本章对树型结构中最简单、应用十分广泛的二叉树结构进行讨论。 6.1定义与性质 6.1.1二叉树的基本概念 1.二叉树 二叉树(Binary Tree)是个有限元素的集合，该集合或者为空、或者由一个称为根(root) 的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。当集合为空时，称该 二叉树为空二叉树。在二叉树中，一个元素也称作一个结点。 二叉树是有序的，即若将其左、右子树颠倒，就成为另一棵不同的二叉树。即使树中 结点只有一棵子树，也要区分它是左子树还是右子树。因此二叉树具有五种基本形态，如 图6.1所示。 左子树 左子树 左子树》 、左子树 (a) (b) (e) (d) 图6.1二叉树的五种基本形态 103

103 第六章 二叉树 在前面几章里讨论的数据结构都属于线性结构，线性结构的特点是逻辑结构简单，易 于进行查找、插入和删除等操作，其主要用于对客观世界中具有单一的前驱和后继的数据 关系进行描述，而现实中的许多事物的关系并非这样简单，如人类社会的族谱、各种社会 组织机构以及城市交通、通讯等，这些事物中的联系都是非线性的，采用非线性结构进行 描绘会更明确和便利。 所谓非线性结构是指，在该结构中至少存在一个数据元素，有两个或两个以上的直接 前驱（或直接后继）元素。树型结构和图型就是其中十分重要的非线性结构，可以用来描 述客观世界中广泛存在的层次结构和网状结构的关系，如前面提到的族谱、城市交通等。 在本书的第六、七、八章将重点讨论这两类非线性结构的有关概念、存储结构、在各种存 储结构上所实施的一些运算以及有关的应用实例。 本章对树型结构中最简单、应用十分广泛的二叉树结构进行讨论。 6.1 定义与性质 6.1.1 二叉树的基本概念 1．二叉树 二叉树（Binary Tree）是个有限元素的集合，该集合或者为空、或者由一个称为根(root) 的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。当集合为空时，称该 二叉树为空二叉树。在二叉树中，一个元素也称作一个结点。 二叉树是有序的，即若将其左、右子树颠倒，就成为另一棵不同的二叉树。即使树中 结点只有一棵子树，也要区分它是左子树还是右子树。因此二叉树具有五种基本形态，如 图 6.1 所示。 (a) (b) (c) (d) (e) 图 6.1 二叉树的五种基本形态 Ф 左子树 左子树 左子树 左子树

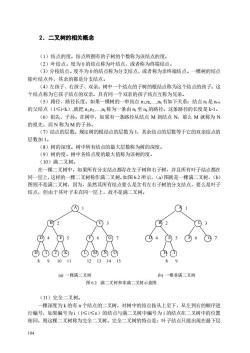
2.二叉树的相关概念 (1)结点的度。结点所拥有的子树的个数称为该结点的度。 (2)叶结点。度为0的结点称为叶结点，或者称为终瑞结点， (3)分枝结点。度不为0的结点称为分支结点，或者称为非终端结点。一棵树的结点 除叶结点外，其余的都是分支结点。 (4)左孩子、右孩子、双亲。树中一个结点的子树的根结点称为这个结点的孩子。这 个结点称为它孩子结点的双亲。具有同一个双亲的孩子结点互称为兄弟。 (5)路径、路径长度。如果一棵树的一串结点n,也，nk有如下关系：结点n是n4 的父结点(1≤i<k),就把n12,.n,称为一条由n至n,的路径。这条路径的长度是k-l。 (6)祖先、子孙。在树中，如果有一条路径从结点M到结点N,那么M就称为N 的祖先，而N称为M的子孙 (7)结点的层数。规定树的根结点的层数为1，其余结点的层数等于它的双亲结点的 层数加1。 (8)树的深度。树中所有结点的最大层数称为树的深度。 (9)树的度。树中各结点度的最大值称为该树的度。 (10)满二叉树。 在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在 同一层上，这样的一棵二叉树称作满二叉树.如图6.2所示，(a)图就是一棵满二叉树，(b) 图则不是满二叉树，因为，虽然其所有结点要么是含有左右子树的分支结点，要么是叶子 结点，但由于其叶子未在同一层上，故不是满二叉树。 01 (B2 B 03 64 (E5 6©7 4 E 5 ①6 ①N ①① 891011 12131415 89 (a一棵满二叉树 ()一棵非满二叉树 图6.2满二叉树和非满二叉树示意图 (11)完全二叉树。 一棵深度为k的有个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进 行编号，如果编号为ⅰ(1≤i≤)的结点与满二叉树中编号为i的结点在二叉树中的位置 相同，则这棵二叉树称为完全二叉树。完全二叉树的特点是：叶子结点只能出现在最下层 104

104 2．二叉树的相关概念 （1）结点的度。结点所拥有的子树的个数称为该结点的度。 （2）叶结点。度为 0 的结点称为叶结点，或者称为终端结点。 （3）分枝结点。度不为 0的结点称为分支结点，或者称为非终端结点。一棵树的结点 除叶结点外，其余的都是分支结点。 （4）左孩子、右孩子、双亲。树中一个结点的子树的根结点称为这个结点的孩子。这 个结点称为它孩子结点的双亲。具有同一个双亲的孩子结点互称为兄弟。 （5）路径、路径长度。如果一棵树的一串结点 n1,n2,.,nk 有如下关系：结点 ni 是 ni+1 的父结点（1≤i<k）,就把 n1,n2,.,nk称为一条由 n1 至 nk 的路径。这条路径的长度是 k-1。 （6）祖先、子孙。在树中，如果有一条路径从结点 M 到结点 N，那么 M 就称为 N 的祖先，而 N 称为 M 的子孙。 （7）结点的层数。规定树的根结点的层数为 1，其余结点的层数等于它的双亲结点的 层数加 1。 （8）树的深度。树中所有结点的最大层数称为树的深度。 （9）树的度。树中各结点度的最大值称为该树的度。 （10）满二叉树。 在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在 同一层上，这样的一棵二叉树称作满二叉树。如图 6.2 所示，（a）图就是一棵满二叉树，（b） 图则不是满二叉树，因为，虽然其所有结点要么是含有左右子树的分支结点，要么是叶子 结点，但由于其叶子未在同一层上，故不是满二叉树。 (a) 一棵满二叉树 (b) 一棵非满二叉树 图 6.2 满二叉树和非满二叉树示意图 （11）完全二叉树。 一棵深度为 k 的有 n 个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进 行编号，如果编号为 i（1≤i≤n）的结点与满二叉树中编号为 i 的结点在二叉树中的位置 相同，则这棵二叉树称为完全二叉树。完全二叉树的特点是：叶子结点只能出现在最下层 A B C D E F G H I J K L M N O A B C D E G H F I 1 5 2 3 4 6 7 8 9 10 11 12 13 14 15 1 2 5 3 6 7 8 9 4

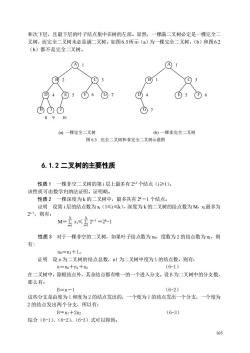
和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二 叉树，而完全二叉树未必是满二叉树。如图6.3所示(a)为一棵完全二叉树，(b)和图62 (b)都不是完全二叉树。 01 1 (2 ©3 ©3 ⊙4©56 ©7 ©5①6 ®①① ©7 89 10 ()一棵完全二叉树 (b) 一棵非完全二又树 图6.3完全二叉树和非完全二叉树示意图 6.1.2二叉树的主要性质 性质1 一棵非空二叉树的第i层上最多有2个结点（≥1）。 该性质可由数学归纳法证明。证明略。 性质2 一棵深度为k的二叉树中，最多具有2一1个结点。 证明设第i层的结点数为X(1≤i≤k),深度为k的二叉树的结点数为M,x最多为 2,则有： M=2x≤言2=2-1 性质3对于一棵非空的二叉树，如果叶子结点数为o,度数为2的结点数为e,则 有 n0=n2+1 证明设n为二叉树的结点总数，nl为二叉树中度为1的结点数，则有： n=n+n十n (6-1) 在二叉树中，除根结点外，其余结点都有唯一的一个进入分支。设B为二叉树中的分支数， 那么有： B=n-1 (6-2) 这些分支是由度为1和度为2的结点发出的，一个度为1的结点发出一个分支，一个度为 2的结点发出两个分支，所以有： B=n1+2n2 (6-3) 综合(6-1)、(6-2，(6-3)式可以得到：

105 和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二 叉树，而完全二叉树未必是满二叉树。如图6.3所示（a）为一棵完全二叉树，（b）和图6.2 （b）都不是完全二叉树。 (a) 一棵完全二叉树 (b) 一棵非完全二叉树 图 6.3 完全二叉树和非完全二叉树示意图 6.1.2 二叉树的主要性质 性质 1 一棵非空二叉树的第 i 层上最多有 2 i-1 个结点（i≥1）。 该性质可由数学归纳法证明。证明略。 性质 2 一棵深度为 k 的二叉树中，最多具有 2 k－1 个结点。 证明 设第 i 层的结点数为 xi（1≤i≤k），深度为 k 的二叉树的结点数为 M，xi最多为 2 i-1，则有： M＝ xi≤ 2 i-1 ＝2 k-1 性质 3 对于一棵非空的二叉树，如果叶子结点数为 n0，度数为 2 的结点数为 n2，则 有: n0＝n2＋1。 证明 设 n 为二叉树的结点总数，n1 为二叉树中度为 1 的结点数，则有： n＝n0＋n1＋n2 （6-1） 在二叉树中，除根结点外，其余结点都有唯一的一个进入分支。设 B 为二叉树中的分支数， 那么有： B＝n－1 （6-2） 这些分支是由度为 1 和度为 2 的结点发出的，一个度为 1 的结点发出一个分支，一个度为 2 的结点发出两个分支，所以有： B＝n1＋2n2 （6-3） 综合（6-1）、（6-2）、（6-3）式可以得到： A B C D E F G H I J A B D C E F G 1 2 4 3 5 6 7 8 9 10 1 1 4 3 5 6 7 k ∑ i=1 k ∑ i=1

no=2+1 性质4具有n个结点的完全二叉树的深度k为logn+1。 证明根据完全二叉树的定义和性质2可知，当一棵完全二叉树的深度为k、结点个 数为n时，有 2*-1-11,则序号为i的结点的双亲结点的序号为i/2(/表示整除)：如果i= 1,则序号为1的结点是根结点，无双亲结点。 (2)如果2i≤n,则序号为i的结点的左孩子结点的序号为2i:如果2i>n,则序号 为i的结点无左孩子。 (3)如果2i+1≤n,则序号为i的结点的右孩子结点的序号为2i+1:如果2i+1)n, 则序号为1的结点无右孩子。 此外，若对二叉树的根结点从0开始编号，则相应的i号结点的双亲结点的编号为(1 -1)/2,左孩子的编号为21十1，右孩子的编号为2i+2。 此性质可采用数学归纳法证明。证明略。 6.2基本操作与存储实现 6.2.1二叉树的存储 1.顺序存储结构 所谓二叉树的顺序存储，就是用一组连续的存储单元存放二叉树中的结点。一般是按 照二叉树结点从上至下、从左到右的顺序存储。这样结点在存储位置上的前驱后继关系并 不一定就是它们在逻辑上的邻接关系，然而只有通过一些方法确定某结点在逻辑上的前驱 结点和后继结点，这种存储才有意义。因此，依据二叉树的性质，完全二叉树和满二叉树 采用顺序存储比较合适，树中结点的序号可以唯一地反映出结点之间的逻辑关系，这样既 能够最大可能地节省存储空间，又可以利用数组元素的下标值确定结点在二叉树中的位置， 106

106 n0＝n2＋1 性质 4 具有 n 个结点的完全二叉树的深度 k 为[log2n]+1。 证明 根据完全二叉树的定义和性质 2 可知，当一棵完全二叉树的深度为 k、结点个 数为 n 时，有 2 k－1－11，则序号为 i 的结点的双亲结点的序号为 i/2(“/”表示整除)；如果 i＝ 1，则序号为 i 的结点是根结点，无双亲结点。 （2）如果 2i≤n，则序号为 i 的结点的左孩子结点的序号为 2i；如果 2i>n，则序号 为 i 的结点无左孩子。 （3）如果 2i＋1≤n，则序号为 i的结点的右孩子结点的序号为2i＋1；如果 2i＋1>n， 则序号为 i 的结点无右孩子。 此外，若对二叉树的根结点从 0 开始编号，则相应的 i 号结点的双亲结点的编号为（i －1）/2，左孩子的编号为2i＋1，右孩子的编号为 2i＋2。 此性质可采用数学归纳法证明。证明略。 6.2 基本操作与存储实现 6.2.1 二叉树的存储 1．顺序存储结构 所谓二叉树的顺序存储，就是用一组连续的存储单元存放二叉树中的结点。一般是按 照二叉树结点从上至下、从左到右的顺序存储。这样结点在存储位置上的前驱后继关系并 不一定就是它们在逻辑上的邻接关系，然而只有通过一些方法确定某结点在逻辑上的前驱 结点和后继结点，这种存储才有意义。因此，依据二叉树的性质，完全二叉树和满二叉树 采用顺序存储比较合适，树中结点的序号可以唯一地反映出结点之间的逻辑关系，这样既 能够最大可能地节省存储空间，又可以利用数组元素的下标值确定结点在二叉树中的位置

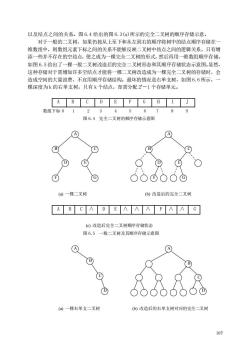
以及结点之间的关系。图6.4给出的图6.3(a)所示的完全二叉树的顺序存储示意。 对于一般的二叉树，如果仍按从上至下和从左到右的顺序将树中的结点顺序存储在 维数组中，则数组元素下标之间的关系不能够反映二叉树中结点之间的逻辑关系，只有增 添一些并不存在的空结点，使之成为一棵完全二叉树的形式，然后再用一维数组顺序存储。 如图6.5给出了一棵一般二叉树改造后的完全二叉树形态和其顺序存储状态示意图。显然， 这种存储对于需增加许多空结点才能将一棵二叉树改造成为一棵完全二叉树的存储时，会 造成空间的大量浪费，不宜用顺序存储结构。最坏的情况是右单支树，如图6.6所示， 棵深度为k的右单支树，只有k个结点，却需分配2一1个存储单元。 ABCDEFGHIJ 数组下标01 6 7 图6.4完全二叉树的顺序存储示意图 ⊙ G B © Q © ò©OO© (a)一棵二叉树 ()改造后的完全二又树 ABC ADE AAAFAAG (@)改造后完全二叉树顺序存储状态 图6.5一般二叉树及其顺序存储示意图 ④ (a)一棵右单支二叉树 )改造后的右单支树对应的完全二叉树 107

107 以及结点之间的关系。图 6.4 给出的图 6.3(a)所示的完全二叉树的顺序存储示意。 对于一般的二叉树，如果仍按从上至下和从左到右的顺序将树中的结点顺序存储在一 维数组中，则数组元素下标之间的关系不能够反映二叉树中结点之间的逻辑关系，只有增 添一些并不存在的空结点，使之成为一棵完全二叉树的形式，然后再用一维数组顺序存储。 如图 6.5 给出了一棵一般二叉树改造后的完全二叉树形态和其顺序存储状态示意图。显然， 这种存储对于需增加许多空结点才能将一棵二叉树改造成为一棵完全二叉树的存储时，会 造成空间的大量浪费，不宜用顺序存储结构。最坏的情况是右单支树，如图 6.6 所示，一 棵深度为 k 的右单支树，只有 k 个结点，却需分配 2 k－1 个存储单元。 A B C D E F G H I J 数组下标 0 1 2 3 4 5 6 7 8 9 图 6.4 完全二叉树的顺序存储示意图 (a) 一棵二叉树 (b) 改造后的完全二叉树 A B C ∧ D E ∧ ∧ ∧ F ∧ ∧ G (c) 改造后完全二叉树顺序存储状态 图 6.5 一般二叉树及其顺序存储示意图 (a) 一棵右单支二叉树 (b) 改造后的右单支树对应的完全二叉树 A B C D E F G A B D C E F G A C B D D C A B

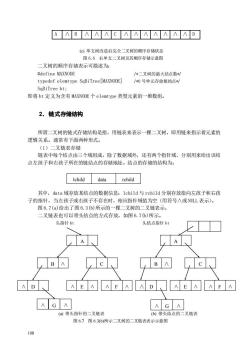
AABAAACAAAAD (⊙)单支树改造后完全二叉树的顺序存储状态 图6.6右单支二叉树及其顺序存储示意图 二叉树的顺序存储表示可描述为： #define MAXNODE /体二又树的最大结点数*制 typedef elemtype SqBiTree[MAXNODE] /0号单元存放根结点/ SqBiTree bt; 即将bt定义为含有MAXNODE个elemtype类型元素的一维数组。 2.链式存储结构 所谓二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示着元素的 逻辑关系。通常有下面两种形式。 (1)二叉链表存储 链表中每个结点由三个域组成，除了数据域外，还有两个指针域，分别用来给出该结 点左孩子和右孩子所在的链结点的存储地址。结点的存储的结构为： Ichild data rchild 其中，d血ta域存放某结点的数据信息：1 lchild与rchild分别存放指向左孩子和右孩 子的指针，当左孩子或右孩子不存在时，相应指针域值为空（用符号∧或NLL表示）。 图6.7(a)给出了图6.36)所示的一棵二叉树的二叉链表示。 二叉链表也可以带头结点的方式存放，如图6.7)所示。 头指针bt 头结点指针bt A A AD、 AEAAFAADAEAAFA AGA (回带头指针的二叉链表 ⑥)带头结点的二叉链表 图6.7图6.3b)所示二叉树的二叉链表表示示意图 108

108 A ∧ B ∧ ∧ ∧ C ∧ ∧ ∧ ∧ ∧ ∧ ∧ D (c) 单支树改造后完全二叉树的顺序存储状态 图 6.6 右单支二叉树及其顺序存储示意图 二叉树的顺序存储表示可描述为： #define MAXNODE /*二叉树的最大结点数*/ typedef elemtype SqBiTree[MAXNODE] /*0 号单元存放根结点*/ SqBiTree bt; 即将 bt 定义为含有 MAXNODE 个 elemtype 类型元素的一维数组。 2．链式存储结构 所谓二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示着元素的 逻辑关系。通常有下面两种形式。 （1）二叉链表存储 链表中每个结点由三个域组成，除了数据域外，还有两个指针域，分别用来给出该结 点左孩子和右孩子所在的链结点的存储地址。结点的存储的结构为： 其中，data 域存放某结点的数据信息；lchild 与 rchild 分别存放指向左孩子和右孩 子的指针，当左孩子或右孩子不存在时，相应指针域值为空（用符号∧或 NULL 表示）。 图 6.7(a)给出了图 6.3(b)所示的一棵二叉树的二叉链表示。 二叉链表也可以带头结点的方式存放，如图 6.7(b)所示。 头指针 bt 头结点指针 bt (a) 带头指针的二叉链表 (b) 带头结点的二叉链表 图 6.7 图 6.3(b)所示二叉树的二叉链表表示示意图 lchild data rchild A B ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ A C D E F D E F B C G ∧ G ∧

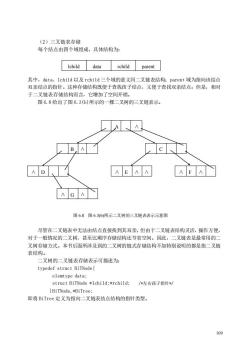
(2)三叉链表存储 每个结点由四个域组成，具体结构为： Ichild data rchild parent 其中，data、lchild以及rchild三个域的意义同二叉又链表结构：parent域为指向该结点 双亲结点的指针。这种存储结构既便于查找孩子结点，又便于查找双亲结点：但是，相对 于二叉链表存储结构而言，它增加了空间开销。 图6.8给出了图6.3(6)所示的一棵二叉树的三叉链表示。 A D AEAA AFA AGA 图6.8图6.3b)所示二叉树的三叉链表表示示意图 尽管在二叉链表中无法由结点直接找到其双亲，但由于二叉链表结构灵活，操作方便， 对于一般情况的二叉树，甚至比顺序存储结构还节省空间。因此，二叉链表是最常用的二 叉树存储方式。本书后面所涉及到的二叉树的链式存储结构不加特别说明的都是指二叉链 表结构。 二叉树的二叉链表存储表示可描述为： typedef struct BiTNode( elemtype data: struct BiTNode*1child:*rchild;/左右孩子指针*/ }BiTNode,*BiTree: 即将BiTree定义为指向二叉链表结点结构的指针类型。 109

109 （2）三叉链表存储 每个结点由四个域组成，具体结构为： 其中，data、lchild 以及 rchild 三个域的意义同二叉链表结构；parent 域为指向该结点 双亲结点的指针。这种存储结构既便于查找孩子结点，又便于查找双亲结点；但是，相对 于二叉链表存储结构而言，它增加了空间开销。 图 6.8 给出了图 6.3(b)所示的一棵二叉树的三叉链表示。 图 6.8 图 6.3(b)所示二叉树的三叉链表表示示意图 尽管在二叉链表中无法由结点直接找到其双亲，但由于二叉链表结构灵活，操作方便， 对于一般情况的二叉树，甚至比顺序存储结构还节省空间。因此，二叉链表是最常用的二 叉树存储方式。本书后面所涉及到的二叉树的链式存储结构不加特别说明的都是指二叉链 表结构。 二叉树的二叉链表存储表示可描述为： typedef struct BiTNode{ elemtype data; struct BiTNode *lchild;*rchild; /*左右孩子指针*/ }BiTNode,*BiTree; 即将 BiTree 定义为指向二叉链表结点结构的指针类型。 lchild data rchild parent A ∧ B ∧ ∧ D ∧ E ∧ ∧ C ∧ F ∧ ∧ G ∧

6.2.2二叉树的基本操作及实现 1,二叉树的基本操作 二叉树的基本操作通常有以下几种： (I)Initiate(bt)建立一棵空二叉树。 (2)Creae(x,It,rbt)生成一棵以x为根结点的数据域信息，以二叉树bt和rb 为左子树和右子树的二叉树。 (3)InsertL(bt,x,parent)将数据域信息为x的结点插入到二叉树bt中作为结点 parent的左孩子结点。如果结点parent原来有左孩子结点，则将结点parent原来的左孩子 结点作为结点x的左孩子结点。 (4)InsertR(bt,x,parent)将数据域信息为x的结点插入到二叉树bt中作为结点 parent的右孩子结点。如果结点parent原来有右孩子结点，则将结点parent原来的右孩子 结点作为结点x的右孩子结点。 (S)DeleteL(bt,parent)在二叉树bt中除结点parent的左子树 (6)DeleteR(bt,parent)在二叉树bt中别除结点parent的右子树。 (7)Search(bt,x)在二叉树bt中查找数据元素x。 (8)Traverse(bt)按某种方式遍历二叉树bt的全部结点。 2.算法的实现 算法的实现依赖于具体的存储结构，当二叉树采用不同的存储结构时，上述各种操作 的实现算法是不同的。下面讨论基于二叉链表存储结构的上述操作的实现算法。 (1)Initiate(bt)初始建立二叉树bt,并使bt指向头结点。在二叉树根结点前建立头 结点，就如同在单链表前建立的头结点，可以方便后边的一些操作实现 int Initiate (BiTree *bt) {初始化建立二叉树bt的头结点* if((*bt=(BiTNode*)malloc(sizeof(BiTNode)-NULL) return0: *ht->lchild=NJ几I *bt->rchild=NULL: return上 算法6.1 110

110 6.2.2 二叉树的基本操作及实现 1．二叉树的基本操作 二叉树的基本操作通常有以下几种： （1）Initiate（bt）建立一棵空二叉树。 （2）Create（x，lbt，rbt）生成一棵以 x 为根结点的数据域信息，以二叉树 lbt 和 rbt 为左子树和右子树的二叉树。 （3）InsertL（bt，x，parent）将数据域信息为 x 的结点插入到二叉树 bt 中作为结点 parent 的左孩子结点。如果结点 parent 原来有左孩子结点，则将结点 parent 原来的左孩子 结点作为结点 x 的左孩子结点。 （4）InsertR（bt，x，parent）将数据域信息为 x 的结点插入到二叉树 bt 中作为结点 parent 的右孩子结点。如果结点 parent 原来有右孩子结点，则将结点 parent 原来的右孩子 结点作为结点 x 的右孩子结点。 （5）DeleteL（bt，parent）在二叉树 bt 中删除结点 parent 的左子树。 （6）DeleteR（bt，parent）在二叉树 bt 中删除结点 parent 的右子树。 （7）Search（bt，x）在二叉树 bt 中查找数据元素 x。 （8）Traverse（bt）按某种方式遍历二叉树 bt 的全部结点。 2．算法的实现 算法的实现依赖于具体的存储结构，当二叉树采用不同的存储结构时，上述各种操作 的实现算法是不同的。下面讨论基于二叉链表存储结构的上述操作的实现算法。 （1）Initiate（bt）初始建立二叉树 bt，并使 bt指向头结点。在二叉树根结点前建立头 结点，就如同在单链表前建立的头结点，可以方便后边的一些操作实现。 int Initiate (BiTree *bt) {/*初始化建立二叉树*bt 的头结点*/ if((*bt=(BiTNode *)malloc(sizeof(BiTNode)))==NULL) return 0; *bt->lchild=NULL; *bt->rchild=NULL; return 1; } 算法 6.1

(2)Creae(x,t,rbt)建立一棵以x为根结点的数据域信息，以二叉树Ibt和rbt 为左右子树的二叉树。建立成功时返回所建二叉树结点的指针：建立失败时返回空指针。 BiTree Create (elemtype x,BiTree lbt,BiTree rbt) {作生成一棵以x为根结点的数据域值以b和t为左右子树的二叉树*/ BiTree p: if((p-(BiTNode+)malloc(sizeof(BiTNode)))=-NULL)return NULL p->data=x, p->Ichild=Ibt p->rchild=rbt: return p. 算法6.2 (3)InsertL (b,x,parent) BiTree InsertL (BiTree bt,elemtype x,BiTree parent) {产在二叉树bt的结点parent的左子树插入结点数据元素x BiTree p: if(parent-NULL) {printf("n插入出错"： return NULL; if((p=(BiTNode*)malloc(sizeof(BiTNode)))=-NULL)return NULL; p->data=x: p->rchild=NULL: if(parent->Ichild-NULL)parent->lchild=p; else p->Ichild=parent->child; parent->Ichild=p; return bt; 算法6.3 (4)InsertR(bt,X,parent)功能类同于(3)，算法略。 (S)DeleteL(bt,parent)在二叉树bt中删除结点parent的左子树。当parent或parent 的左孩子结点为空时删除失败。别除成功时返回根结点指针：删除失败时返回空指针。 BiTree DeleteL (BiTree bt,BiTree parent) {/在二叉树bt中刷除结点parent的左子树/ BiTree P. 111

111 （2）Create（x，lbt，rbt）建立一棵以 x 为根结点的数据域信息，以二叉树 lbt 和 rbt 为左右子树的二叉树。建立成功时返回所建二叉树结点的指针；建立失败时返回空指针。 BiTree Create（elemtype x，BiTree lbt，BiTree rbt） {/*生成一棵以x 为根结点的数据域值以 lbt 和 rbt 为左右子树的二叉树*/ BiTree p; if ((p=(BiTNode *)malloc(sizeof(BiTNode)))==NULL) return NULL; p->data=x; p->lchild=lbt; p->rchild=rbt; return p; } 算法 6.2 （3）InsertL（bt，x，parent） BiTree InsertL（BiTree bt，elemtype x，BiTree parent） {/*在二叉树 bt 的结点 parent 的左子树插入结点数据元素 x*/ BiTree p; if (parent==NULL) { printf(“\n 插入出错”)； return NULL; } if ((p=(BiTNode *)malloc(sizeof(BiTNode)))==NULL) return NULL; p->data=x; p->lchild=NULL; p->rchild=NULL; if (parent->lchild==NULL) parent->lchild=p; else {p->lchild=parent->lchild; parent->lchild=p; } return bt; } 算法 6.3 （4）InsertR（bt，x，parent）功能类同于（3），算法略。 （5）DeleteL（bt，parent）在二叉树 bt 中删除结点 parent 的左子树。当parent 或parent 的左孩子结点为空时删除失败。删除成功时返回根结点指针；删除失败时返回空指针。 BiTree DeleteL（BiTree bt，BiTree parent） {/*在二叉树 bt 中删除结点 parent 的左子树*/ BiTree p;

if(parent-=NULLJparent->Ichild-NULL) {printf("n删除出错")： return NULL' p=parent->Ichild; parent->lchild=NULL: fce(p以当p为叶子结点时，这样删除仅释放了所子树根结点的空间，/ 小若要别除子树分支中的结点，需用后面介绍的遍历操作来实现。/ return br, 算法6.4 (6)DeleteR(bt,parent)功能类同于(S),只是除结点parent的右子树。算法略 操作Search(bt,x)实际是遍历操作Traverse(bt)的特例，关于二叉树的遍历操作 的实现，将在下一节中重点介绍。 6.3二叉树的遍历 6.3.1二叉树的遍历方法及递归实现 二叉树的遍历是指按照某种顺序访问二叉树中的每个结点，使每个结点被访问一次且 仅被访问一次。 遍历是二叉树中经常要用到的一种操作。因为在实际应用问题中，常常需要按一定顺 序对二叉树中的每个结点逐个进行访问，查找具有某一特点的结点，然后对这些满足条件 的结点进行处理。 通过一次完整的遍历，可使二叉树中结点信息由非线性排列变为某种意义上的线性序 列。也就是说，遍历操作使非线性结构线性化。 由二叉树的定义可知，一 棵由根结点、根结点的左子树和根结点的右子树三部分组成。 因此，只要依次遍历这三部分，就可以遍历整个二叉树。若以D、L、R分别表示访问根 结点、遍历根结点的左子树、遍历根结点的右子树，则二叉树的遍历方式有六种：DLR、 LDR、LRD、DRL、RDL和RLD。如果限定先左后右，则只有前三种方式，即DLR(称 为先序遍历)、LDR(称为中序遍历)和LRD(称为后序遍历)。 112

112 if (parent==NULL||parent->lchild==NULL) { printf(“\n 删除出错”)； return NULL’ } p=parent->lchild; parent->lchild=NULL; free(p); /*当 p 为非叶子结点时，这样删除仅释放了所删子树根结点的空间，*/ /*若要删除子树分支中的结点，需用后面介绍的遍历操作来实现。*/ return br; } 算法 6.4 （6）DeleteR（bt，parent）功能类同于（5），只是删除结点 parent 的右子树。算法略。 操作 Search（bt，x）实际是遍历操作 Traverse（bt）的特例，关于二叉树的遍历操作 的实现，将在下一节中重点介绍。 6.3 二叉树的遍历 6.3.1 二叉树的遍历方法及递归实现 二叉树的遍历是指按照某种顺序访问二叉树中的每个结点，使每个结点被访问一次且 仅被访问一次。 遍历是二叉树中经常要用到的一种操作。因为在实际应用问题中，常常需要按一定顺 序对二叉树中的每个结点逐个进行访问，查找具有某一特点的结点，然后对这些满足条件 的结点进行处理。 通过一次完整的遍历，可使二叉树中结点信息由非线性排列变为某种意义上的线性序 列。也就是说，遍历操作使非线性结构线性化。 由二叉树的定义可知，一棵由根结点、根结点的左子树和根结点的右子树三部分组成。 因此，只要依次遍历这三部分，就可以遍历整个二叉树。若以 D、L、R 分别表示访问根 结点、遍历根结点的左子树、遍历根结点的右子树，则二叉树的遍历方式有六种：DLR、 LDR、LRD、DRL、RDL 和 RLD。如果限定先左后右，则只有前三种方式，即 DLR（称 为先序遍历）、LDR（称为中序遍历）和 LRD（称为后序遍历）