大连理工大学：《数据结构》课程教学课件（PPT讲稿）第三章 栈和队列

第三章栈和队列 栈和队列是两种特殊的线性表，是操作受限的线性 表，称限定性DS §3.1栈(stack) ★栈的定义和特点 必定义：1 限定仅在表尾进行插入或删除操作的线性表， 表尾一栈顶，表头一栈底，不含元素的空表称空栈 必特点： 先进后出(FLO)或后进先出(LFO) 进栈 出栈 栈顶 an 栈s=(al,a2,.,an) a2 栈底 al

第三章 栈和队列 栈和队列是两种特殊的线性表，是操作受限的线性 表，称限定性DS §3.1 栈（stack） 栈的定义和特点 ❖定义：限定仅在表尾进行插入或删除操作的线性表， 表尾—栈顶，表头—栈底，不含元素的空表称空栈 ❖特点：先进后出（FILO）或后进先出（LIFO） an a1 a2. 栈底 栈顶 进栈 . 出栈 栈s=(a1,a2,.,an)

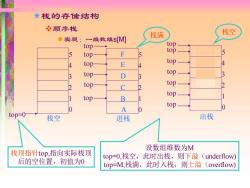
★栈的存储结构 冬顺序栈 栈满 栈空 ●实现： 一维数组s[M] top top 5 top F top 5 4 top E 4 top 4 top D top 3 3 3 2 top c top 2 top top B top 0 top=0 栈空 进栈 出栈 设数组维数为M 栈顶指针top,指向实际栈顶 top=O,栈空，此时出栈，则下溢 (underflow) 后的空位置，初值为0 top=M,栈满，此时入栈，则上溢(overflow)

栈的存储结构 ❖顺序栈 ⚫实现：一维数组s[M] top=0 1 2 3 4 5 0 栈空 栈顶指针top,指向实际栈顶 后的空位置，初值为0 top 1 2 3 4 5 0 进栈 A top 出栈 栈满 B C D E F 设数组维数为M top=0,栈空，此时出栈，则下溢（underflow) top=M,栈满，此时入栈，则上溢（overflow) top top top top top 1 2 3 4 5 A 0 B C D E top F top top top top top 栈空

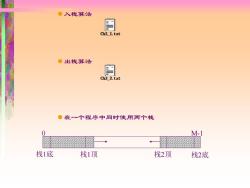
●入栈算法 目 Ch3_1.txt ●出栈算法 Ch3 2.txt ●在一个程序中同时使用两个栈 M-1 栈1底 栈1项 栈2顶 栈2底

⚫入栈算法 0 M-1 栈1底 栈1顶 栈2顶 栈2底 ⚫出栈算法 ⚫在一个程序中同时使用两个栈

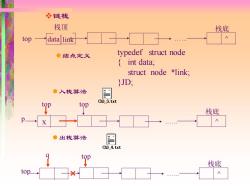
链栈 栈顶 栈底 top data link ●结点定义 typedef struct node int data; struct node *link; JD: ●入栈算法 周 Ch3 3.txt top 栈底 p ●出栈算法 Ch3 4.txt q top 栈底 top

❖链栈 栈顶 top data link . ^ 栈底 ⚫结点定义 ⚫入栈算法 ⚫出栈算法 typedef struct node { int data; struct node *link; }JD; . ^ 栈底 top top x p top . ^ 栈底 top q

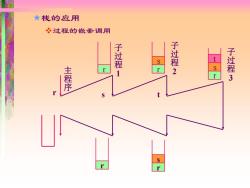
★栈的应用 冬过程的嵌套调用 子过程 主 子过程2 子过程3 r

栈的应用 ❖过程的嵌套调用 r 主 程 序 s r r r s 子 过 程 1 r s t 子 过 程 2 r s t 子 过 程 3

必递归过程及其实现 ●递归：函数直接或间接的调用自身叫~ ●实现：建立递归工作栈 例 递归的执行情况分析 void print(int w) { int i; if(w!=0) 运行结果： { print(w-1); 1, for(i=1;i<-w;++i) 2,2, printf(%3d,”,w); 3,3,3, printf(“/n”); Ch3 10.c →

例 递归的执行情况分析 ❖递归过程及其实现 ⚫递归：函数直接或间接的调用自身叫~ ⚫实现：建立递归工作栈 void print(int w) { int i; if ( w!=0) { print(w-1); for(i=1;i<=w;++i) printf(“%3d,”,w); printf(“/n”); } } Ch3_10.c 运行结果： 1， 2，2， 3，3，3

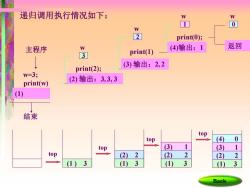
递归调用执行情况如下： 卫 0 W 2 print(O); 主程序 w (4)输出：1 返回 3 print(1) print(2); (3)输出：2,2 w=3; (2)输出：3,3,3 print(w) (1) 结束 top top (4) top (3) 3) top (2) 2 2 2) (1)3 (1)3 3 (1) 3 Back

递归调用执行情况如下： 主程序 (1) print(w) w=3; 3 print(2); （1）w=3 top (2) 输出：3, 3, 3 w 2 print(1) ; （2）w=2 （1）w=3 top (3) 输出：2, 2 w 1 print(0); （3）w=1 （2）w=2 （1）w=3 top (4)输出：1 w 0 （4）w=0 （3）w=1 （2）w=2 （1）w=3 top w (3) 输出：2, 2 (2) 2 (1) 3 top (4)输出：1 (3) 1 (2) 2 (1) 3 top (2) 输出：3, 3, 3 (1 ) 3 top 返回 (3) 1 (2) 2 (1) 3 top (4) 0 结束 (1)

Tower of Hanoi问题 ●问题描述：有A,B,C三个塔座，A上套有个直径不同的圆盘，按 直径从小到大叠放，形如宝塔，编号1,2,3.门。要求将个圆盘 从A移到C,叠放顺序不变，移动过程中遵循下列原则： ◆每次只能移一个圆盘 ◆圆盘可在三个塔座上任意移动 ◆任何时刻，每个塔座上不能将大盘压到小盘上 ●解决方法： ◆n=1时，直接把圆盘从A移到C ◆n>1时，先把上面n-1个圆盘从A移到B,然后将n号盘从A 移到C,再将-1个盘从B移到C。即把求解个圆盘的 Hanoi问题转化为求解n-1个圆盘的Hanoi问题，依次类 推，直至转化成只有一个圆盘的Hanoi,问题 ●算法： Hanoi.txt ●执行情况： ◆递归工作栈保存内容：形参，Xy,Z和返回地址 ◆返回地址用行编号表示 Z 返回地址

❖Tower of Hanoi问题 ⚫问题描述：有A,B,C三个塔座，A上套有n个直径不同的圆盘，按 直径从小到大叠放，形如宝塔,编号1,2,3.n。要求将n个圆盘 从A移到C，叠放顺序不变，移动过程中遵循下列原则： ◆每次只能移一个圆盘 ◆圆盘可在三个塔座上任意移动 ◆任何时刻，每个塔座上不能将大盘压到小盘上 ⚫解决方法： ◆n=1时，直接把圆盘从A移到C ◆n>1时，先把上面n-1个圆盘从A移到B,然后将n号盘从A 移到C,再将n-1个盘从B移到C。即把求解n个圆盘的 Hanoi问题转化为求解n-1个圆盘的Hanoi问题，依次类 推，直至转化成只有一个圆盘的Hanoi问题 ⚫算法： ⚫执行情况： ◆递归工作栈保存内容：形参n,x,y,z和返回地址 ◆返回地址用行编号表示 n x y z 返回地址

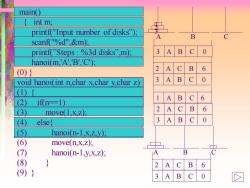
main() int m: printf("Input number of disks); B scanf("%d"&m); printf"Steps %3d disks",m): 3 A hanoi(m.'AB''C): 2 (0)} A C B 6 void hanoi(int n,char x,char y,char z) 3 A B C 0 (1) 1 A B C 6 (2) if(n-1) (3) A C B 6 move(1,x,z); 2 (4) else 3 A B C 0 (5) hanoi(n-1,x,Z,y); (6) move(n,x,z); (7) hanoi(n-1,y,x,Z); A B (8) 2 A C B 6 (9)} 3A B C 0

main() { int m; printf("Input number of disks”); scanf("%d",&m); printf(”Steps : %3d disks”,m); hanoi(m,'A','B','C'); (0) } void hanoi(int n,char x,char y,char z) (1) { (2) if(n==1) (3) move(1,x,z); (4) else{ (5) hanoi(n-1,x,z,y); (6) move(n,x,z); (7) hanoi(n-1,y,x,z); (8) } (9) } A B C 1 2 3 3 A B C 0 3 A B C 0 2 A C B 6 3 A B C 0 2 A C B 6 1 A B C 6 A B C 3 A B C 0 2 A C B 6

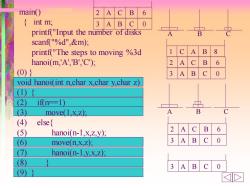
main() 2A C B 6 { int m; 3A .B 0 printf("Input the number of disks scanf("%d",&m); printf("The steps to moving %3d C A B 8 hanoi(m,'A,B','C); 2 A C B 6 (0)} A 3 B 0 void hanoi(int n,char xchar y,char z) (1) (2ù if(n==1) (3) move(1,x,Z); A (4) else (5) hanoi(n-1,x,z,y); 2 A B (6) move(n,x,Z); 3 A B (⑦ hanoi(n-1,y,xZ); (8) 3 A B (9)

main() { int m; printf("Input the number of disks scanf("%d",&m); printf("The steps to moving %3d hanoi(m,'A','B','C'); (0) } void hanoi(int n,char x,char y,char z) (1) { (2) if(n==1) (3) move(1,x,z); (4) else{ (5) hanoi(n-1,x,z,y); (6) move(n,x,z); (7) hanoi(n-1,y,x,z); (8) } (9) } A B C 3 A B C 0 2 A C B 6 1 C A B 8 A B C 3 A B C 0 2 A C B 6 3 A B C 0 3 A B C 0 2 A C B 6