大连理工大学：《数据结构》课程教学课件（PPT讲稿）第四章 数组

第四章数组 数组可以看成是一种特殊的线性表，即线性表中数 据元素本身也是一个线性表 §4.1数组的定义和特点 (a11 a12 au) ★定义 (a21 a22 心 ★数组特点 数组结构固定 数据元素同构 ★数组运算 必给定一组下标，存取相应的数据元素 给定一组下标，修改数据元素的值

第四章 数组 数组可以看成是一种特殊的线性表，即线性表中数 据元素本身也是一个线性表 §4.1 数组的定义和特点 定义                  = m m mn n n m n a a a a a a a a a A . . . . . . . . . . . 1 2 21 22 2 11 12 1 数组特点 ❖数组结构固定 ❖数据元素同构 数组运算 ❖给定一组下标，存取相应的数据元素 ❖给定一组下标，修改数据元素的值 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )

§4.2数组的顺序存储结尥 ★次) 0 a11 按列序为主序存放 a24 。n■量量■量 m- am1 m a12 a11 a12 a22 a21 a22 。●●●●●●● 220 造■道■■■面 am2 &m1 am2 ·●●●0. 8m0 ain a20 Loc(aij)=Loc(a)+[(j-1)m+(i-1)]*I 多”进进想数装 m*n-1 amn

§4.2 数组的顺序存储结构 次序约定 ❖以行序为主序 ❖以列序为主序 a11 a12 . a1n a21 a22 . a2n am1 am2 . amn . Loc( aij)=Loc(a11)+[(i-1)n+(j-1)]*l 按行序为主序存放 amn . am2 am1 . a2n . a22 a21 a1n . a12 0 a11 1 n-1 m*n-1 n 按列序为主序存放 0 1 m-1 m*n-1 m amn . a2n a1n . am2 . a22 a12 am1 . a21 a11 a11 a12 . a1n a21 a22 . a2n am1 am2 . amn . Loc(aij)=Loc(a11)+[(j-1)m+(i-1)]*l

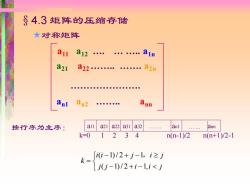
§4.3矩阵的压缩存储 ★对称矩阵 a11 a12. 810 a21 a22.a2n 。0.0e。●s●。e00●0●● Anl an2 ●●●●●●9● Ann 按行序为主序： all a21 a22 a31 a32 anl ann k=0 1234 n(n-1)/2 n(n+1)/2-1 ii-1)/2+j-1,i≥j k= j(U-1)/2+i-1,i<j

§4.3 矩阵的压缩存储 对称矩阵    − + −  − + −  = j j i i j i i j i j k ( 1)/ 2 1, ( 1)/ 2 1， a11 a12 . . . a1n a21 a22. . a2n an1 an2 . ann . a11 a21 a22 a31 a32 . an1 . ann k=0 1 2 3 4 n(n-1)/2 n(n+1)/2-1 按行序为主序：

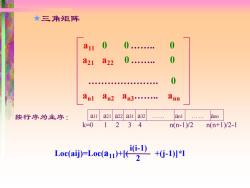
★三角矩阵 a11 0 a21 a22 0. 0 Anl an2 an3. 3n0 按行序为主序： all a21a22a31a32 anl ann k=0 1234 n(n-1)/2 n(n+1)/2-1 Loc(aij)-Loe()D+-1)

三角矩阵 a11 0 0 . 0 a21 a22 0 . 0 an1 an2 an3. ann . 0 Loc(aij)=Loc(a11)+[( +(j-1)]*l i(i-1) 2 a11 a21 a22 a31 a32 . an1 . ann k=0 1 2 3 4 n(n-1)/2 n(n+1)/2-1 按行序为主序：

★对角矩阵 a11 a120 821 a22 a23 0 a32 a33 a340. 0 0 0.an-1,n-2 an-1,n-1 an-1,n 0 0 .ann-1 Ann. 按行序为主序： all a12 a21a22a23 g。, ann-1 ann k=0 1234 n(n-1)/2 n(n+1)/2-1 L0c(aij)=Loc(a1u)+2(i-1)+(j-1)

对角矩阵 a11 a12 0 . . 0 a21 a22 a23 0 . 0 0 0. an-1,n-2 an-1,n-1 an-1,n 0 0 . .an,n-1 ann. 0 a32 a33 a34 0 . 0 . Loc(aij)=Loc(a11)+2(i-1)+(j-1) a11 a12 a21 a22 a23 . . ann-1 ann k=0 1 2 3 4 n(n-1)/2 n(n+1)/2-1 按行序为主序：

★稀疏矩阵 ?定义：非零元较零元少，且分布没有一定规律的矩阵 必压缩存储原则：只存矩阵的行列维数和每个非零元的 行列下标及其值 0 129 0 00 0 0 0 0 0 0 0 0 -3 0 0 0 0140 M= 0 0 24 0 0 0 0 0 18 0 0 00 0 15 0 0 -70 0 06x1 M由{(1,2,12)，(1,3,9)，(3,1，-3)，(3,6,14)，(4,3,24)， (5,2,18),(6,1,15),(6,4,-7)}和矩阵维数(6,7)唯一确定

15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M = M由{(1,2,12), (1,3,9), (3,1,-3), (3,6,14), (4,3,24), (5,2,18), (6,1,15), (6,4,-7) } 和矩阵维数（6,7）唯一确定 稀疏矩阵 ❖定义：非零元较零元少，且分布没有一定规律的矩阵 ❖压缩存储原则：只存矩阵的行列维数和每个非零元的 行列下标及其值

冬稀疏矩阵的压缩存储方法 0 129000 0> 0 00 000 0 ●顺序存储结构 -3 0 0 0 014 0 M= #define M20 0 024 0 00 0 ◆三元组表 typedef struct node 0 1800 00 0 行列下标 非零元值 { int ij 15 00-700 int v, JD; 0 6 7 8 JD ma[M]; 2 12 ma0].i,ma[0]j,ma[0]v分别存放 2 3 9 矩阵行列维数和非零元个数 3 1 -3 3 3 6 14 4 3 24 5 5 2 18 三元组表所需存储单元个数为3（什1） 6 其中t为非零元个数 6 1 15 7 6 4 -7 8 ma

❖稀疏矩阵的压缩存储方法 ⚫顺序存储结构 ◆三元组表 #define M 20 typedef struct node { int i,j; int v; }JD; JD ma[M]; 三元组表所需存储单元个数为3(t+1) 其中t为非零元个数 6 7 8 1 2 12 1 3 9 3 1 -3 3 6 14 4 3 24 5 2 18 6 1 15 6 4 -7 ma i j v 0 1 2 3 4 5 6 7 8 ma[0].i,ma[0].j,ma[0].v分别存放 矩阵行列维数和非零元个数 行列下标 非零元值 15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M =

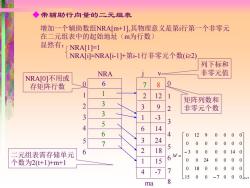
◆带辅助行向量的二元组表 增加一个辅助数组NRA[m+1],其物理意义是第i行第一个非零元 在二元组表中的起始地址(m为行数) 显然有：NRA[I]=I NRA[门=NRA[i-1]+第i-1行非零元个数（≥2） 列下标和 NRA 非零元值 NRA[O]不用或 存矩阵行数 6 7 8 2 12 1 矩阵列数和 2 3 3 9 2 非零元个数 3 3 -3 5 3 4 6 14 6 4 0 129 0000 5 3 24 5 00 0 000 2 二元组表需存储单元 18 1 15 6M= -3 0 0 00140 个数为2(t+1)+m+1 0 024。 000 0 4 -7 7 0180 000 0 L15 00-70006x7 ma 8

◆带辅助行向量的二元组表 增加一个辅助数组NRA[m+1],其物理意义是第i行第一个非零元 在二元组表中的起始地址（m为行数） 显然有： NRA[1]=1 NRA[i]=NRA[i-1]+第i-1行非零元个数(i2) 0 1 2 3 4 5 6 NRA 1 3 3 5 6 7 6 7 8 2 12 3 9 1 -3 6 14 3 24 2 18 1 15 4 -7 ma j v 0 1 2 3 4 5 6 7 8 矩阵列数和 非零元个数 列下标和 非零元值 NRA[0]不用或 存矩阵行数 二元组表需存储单元 个数为2(t+1)+m+1 15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M =

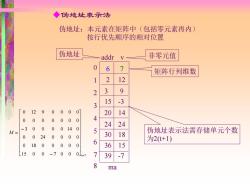
◆伪地址表示法 伪地址： 本元素在矩阵中（包括零元素再内） 按行优先顺序的相对位置 伪地址 addr 非零元值 0 6 7 矩阵行列维数 1 2 12 2 3 9 15 3 0 12 9 000 0 20 14 0 0 0 0 00 0 24 24 -30 0 0 0140 M= 5 30 18 伪地址表示法需存储单元个数 0 024 0 0 0 0 6 为2(t+1) 0 1800 0 0 0 36 15 15 0 0 -70 0 0J6x1 7 39 -7 8 ma

◆伪地址表示法 伪地址：本元素在矩阵中（包括零元素再内） 按行优先顺序的相对位置 6 7 2 12 3 9 15 -3 20 14 24 24 30 18 36 15 39 -7 ma 伪地址 addr v 非零元值 矩阵行列维数 0 1 2 3 4 5 6 7 8 伪地址表示法需存储单元个数 为2(t+1) 15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M =

◆求转置矩阵 问题描述：已知一个稀疏矩阵的三元组表，求该矩 阵转置矩阵的三元组表 问题分析 一投矩阵转置算法： for(col=0;col<n;col++) for(row-0;row<m;row++) n[col][row]=m[row][col]: T(n)=0(mxn)

◆求转置矩阵 问题描述：已知一个稀疏矩阵的三元组表，求该矩 阵转置矩阵的三元组表 问题分析 一般矩阵转置算法： for(col=0;col<n;col++) for(row=0;row<m;row++) n[col][row]=m[row][col]; T(n)=O(mn)