厦门大学：《数据结构》课程教学课件（PPT讲稿）第六章 树和二叉树

数据结构

数据结构

第六章树和二叉树 6.1树的定义和基本概念 6. 2二叉树 6.2.1树的定义和基本术语 6.2.2二叉树的性质 6.2.3二叉树的存储结构 6.3遍历二叉树 6.3.1遍历二叉树 6.3.2线索二叉树 6.4树和森林 6.4.1树的存储结构 6.4.2森林与二叉树的转换

第六章 树和二叉树 6.1 树的定义和基本概念 6.2 二叉树 6.2.1 树的定义和基本术语 6.2.2 二叉树的性质 6.2.3 二叉树的存储结构 6.3 遍历二叉树 6.3.1 遍历二叉树 6.3.2 线索二叉树 6.4 树和森林 6.4.1 树的存储结构 6.4.2 森林与二叉树的转换

6.4.3树和森林的遍历 6.6赫夫曼树及其应用 6.6.1最优二叉树（赫夫曼树） 6.6.2赫夫曼编码

6.4.3树和森林的遍历 6.6 赫夫曼树及其应用 6.6.1 最优二叉树（赫夫曼树） 6.6.2 赫夫曼编码

树型结构是一类重要的非线性结构。树型结 构是结点之间有分支，并且具有层次关系的结构 它非常类似于自然界中的树。树结构在客观世界 国是大量存在的，例如家谱、行政组织机构都可 用树形象地表示。树在计算机领域中也有着广泛 的应用，例如在编译程序中，用树来表示源程序 的语法结构；在数据库系统中，可用树来组织信 息；在分析算法的行为时，可用树来描述其执行 过程。等等。 6.1树的定义和基本术语 定义：树Tree)是n(n>=0)个结点的有限集T,T 为空时称为空树，否则它满足如下两个条件： (1)有且仅有一个特定的称为根(Root)的结点

树型结构是一类重要的非线性结构。树型结 构是结点之间有分支，并且具有层次关系的结构， 它非常类似于自然界中的树。树结构在客观世界 国是大量存在的，例如家谱、行政组织机构都可 用树形象地表示。树在计算机领域中也有着广泛 的应用，例如在编译程序中，用树来表示源程序 的语法结构；在数据库系统中，可用树来组织信 息；在分析算法的行为时，可用树来描述其执行 过程。等等。 6.1 树的定义和基本术语 定义：树(Tree)是n(n>=0)个结点的有限集T，T 为空时称为空树，否则它满足如下两个条件： （1）有且仅有一个特定的称为根(Root)的结点；

(2)其余的结点可分为m(m>=0)个互不相交的子集 T1T2T3TmT1T2,T3.Tm,其中每个子集又是 棵树，并称其为子树(Subtree)。如图6.1 树还有其他的表示形式，如图6.2的三种表示法： (1)嵌套集合(2)广义表的形式(3)凹入表示 法 下面是树结构的一些基本术语： 度：结点拥有的子树称为结点的度。 叶子（终端结点）：度为0的结点。其余结点称为非 终端结点或分支结点。 树的度：树内各结点的度的最大值。 孩子：结点的子树的根称为该结点的孩子。相应地 该结点称为双亲。同一个双亲的孩子称为兄弟。 依此可以递归定义祖先和子孙的概念

(2)其余的结点可分为m(m>=0)个互不相交的子集 T1,T2,T3.Tm T1,T2,T3.Tm，其中每个子集又是一 棵树，并称其为子树(Subtree)。如图6.1 树还有其他的表示形式，如图6.2的三种表示法： （1）嵌套集合（2）广义表的形式（3）凹入表示 法 下面是树结构的一些基本术语： 度：结点拥有的子树称为结点的度。 叶子（终端结点）：度为0的结点。其余结点称为非 终端结点或分支结点。 树的度：树内各结点的度的最大值。 孩子：结点的子树的根称为该结点的孩子。相应地， 该结点称为双亲。同一个双亲的孩子称为兄弟。 依此可以递归定义祖先和子孙的概念

■ 结点的层次：从根开始定义，根为第一层，根的 孩子为第二层。若某个结点在第层，则其子树的 根就在第1+1层。双亲在同一层的结点互为堂兄弟。 树中结点的最大层次称为树的深度或高度。 有序树：如果该树中结点的各子树看成从左至右 是有次序的，则该树称为有序树。否则称为无序 树 森林：是m(m>=0)棵互不相交的树的集合。对 树中每个结点而言，其子树的集合即为森林。 由 此，可以森林和树相互递归的定义来描述树。 Tree=(root,),其中F是m棵树的森林。 F=(T1,T2,T3.Tm),其中T称做根root的第i棵子树

◼ 结点的层次：从根开始定义，根为第一层，根的 孩子为第二层。若某个结点在第l层，则其子树的 根就在第l+1层。双亲在同一层的结点互为堂兄弟。 树中结点的最大层次称为树的深度或高度。 ◼ 有序树：如果该树中结点的各子树看成从左至右 是有次序的，则该树称为有序树。否则称为无序 树。 ◼ 森林：是m（m>=0）棵互不相交的树的集合。对 树中每个结点而言，其子树的集合即为森林。由 此，可以森林和树相互递归的定义来描述树。 Tree=(root, F)，其中F是m棵树的森林。 F=(T1,T2,T3.Tm)，其中Ti称做根root的第i棵子树

6.2二叉树 二叉树在树结构的应用中起着非常重要的作 用，因为对二叉树的许多操作算法简单，而任何 树都可以与二叉树相互转换，这样就解决了树的 存储结构及其运算中存在的复杂性。 62.1二叉树的定义 定义：二叉树是由n(n>=0)个结点的有限集合构 成，此集合或者为空集 , 或者由一个根结点及两 棵互不相交的左右子树组成，并且左右子树都是 二叉树，且次序不能任意颠倒。 这也是一个递归定义。二叉树可以是空集合 根可以有空的左子树或空的右子树。二叉树不是 树的特殊情况，它们是两个概念

6.2 二叉树 二叉树在树结构的应用中起着非常重要的作 用，因为对二叉树的许多操作算法简单，而任何 树都可以与二叉树 相互转换，这样就解决了树的 存储结构及其运算中存在的复杂性。 6.2.1 二叉树的定义 定义：二叉树是由n(n>=0)个结点的有限集合构 成，此集合或者为空集，或者由一个根结点及两 棵互不相交的左右子树组成，并且左右子树都是 二叉树，且次序不能任意颠倒。 这也是一个递归定义。二叉树可以是空集合， 根可以有空的左子树或空的右子树。二叉树不是 树的特殊情况，它们是两个概念

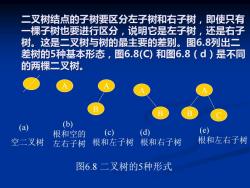
二叉树结点的子树要区分左子树和右子树，即使只有 一棵子树也要进行区分，说明它是左子树，还是右子 树。这是二叉树与树的最主要的差别。图6.8列出二 差树的5种基本形态，图6.8(C)和图6.8(d)是不同 的两棵二叉树。 B (a） (b) 根和空的 (c) (d) (e) 空二叉树 左右子树 根和左子树 根和右子树 根和左右子树 图6.8二叉树的5种形式

二叉树结点的子树要区分左子树和右子树，即使只有 一棵子树也要进行区分，说明它是左子树，还是右子 树。这是二叉树与树的最主要的差别。图6.8列出二 差树的5种基本形态，图6.8(C) 和图6.8（d）是不同 的两棵二叉树。 (a) 空二叉树 A A B A B A B C (b) 根和空的 左右子树 (c) 根和左子树 (d) 根和右子树 (e) 根和左右子树 图6.8 二叉树的5种形式

6.2.2二叉树的性质 二叉树具有下列重要性质： 性质1：在二叉树的第i层上至多有21个结点(>=1)。 采用归纳法证明此性质。 当i=1时，只有一个根结点，21=2°=1，命题成立。 现在假定对于所有的j,1<=j<i,命题成立，即第j层 上至多有21个结点，那么可以证明j=时命题也成 立。由归纳假设可知，第i-1层上至多有22个结点。 由于二叉树每个结点的度最大为2，故在第层上最 大结点数为第-1层上最大结点数的二倍， 即2×2-2=2-1。命题得到证明

6.2.2 二叉树的性质 二叉树具有下列重要性质： 性质1： 在二叉树的第i层上至多有2 i-1个结点(i>=1)。 采用归纳法证明此性质。 当i=1时，只有一个根结点，2 i-1=20 =1,命题成立。 现在假定对于所有的j，1<=j<i,命题成立，即第j层 上至多有2 j-1个结点，那么可以证明j＝i时命题也成 立。由归纳假设可知，第i－1层上至多有2 i-2个结点。 由于二叉树每个结点的度最大为2，故在第i层上最 大结点数为第i－1层上最大结点数的二倍， 即2×2 i-2＝2 i-1。命题得到证明

性质2：深度为k的二叉树至多有2水-1个结点 (k>=1): 深度为k的二叉树的最大的结点时为二叉树中每层上 的最大结点数之和，由性质1得到每层上的最大结点 数：E11(第层上的最大结点数)=E=12-1=2水- 1 性质3：对任何一棵二叉树，如果其终端结点数为 n0,度为2的结点数为n2,则n0=n2+1。 设二叉树中度为1的结点数为n1,二叉树中总结点数 为N,因为二叉树中所有结点均小于或等于2，所以 有：N=no+n1+n2 (6-1) 再看二叉树中的分支数，除根结点外，其余结点都 有一个进入分支，设B为二叉树中的分支总数，则 有：N=B+1

性质2：深度为k的二叉树至多有2 k－1个结点 （k>=1). 深度为k的二叉树的最大的结点时为二叉树中每层上 的最大结点数之和，由性质1得到每层上的最大结点 数：E k I=1（第i层上的最大结点数）= Ek I=12 i-1=2k – 1 性质3： 对任何一棵二叉树，如果其终端结点数为 n0，度为2的结点数为n2，则n0＝n2＋1。 设二叉树中度为1的结点数为n1，二叉树中总结点数 为N，因为二叉树中所有结点均小于或等于2，所以 有：N＝n0＋n1＋n2 (6-1) 再看二叉树中的分支数，除根结点外，其余结点都 有一个进入分支，设B为二叉树中的分支总数， 则 有：N＝B＋1