《数据结构》课程PPT教学课件（2012）第6章 树和二叉树 Tree & Binary Tree（2/4）

第6章树和二叉树 CTree Binary Tree) 二叉树的定义、 6.1 树的基本概念 性质和存储结构 6.2 二叉树 6.3遍历二叉树和线索二叉树 6.4 树和森林 二叉树的运算 6.5 赫夫曼树及其应用

1 第6章 树和二叉树 （Tree & Binary Tree） 6.1 树的基本概念 6.2 二叉树 6.3 遍历二叉树和线索二叉树 6.4 树和森林 6.5 赫夫曼树及其应用 二叉树的定义、 性质和存储结构 二叉树的运算

6.2二叉树 6.2.1二叉树的定义 6.2.2二叉树的性质 6.2.3二叉树的存储结构 为何要重点研究每结点最多只有两个“叉”的树？ 二叉树的结构最简单，规律性最强： 可以证明，所有树都能转为唯一对应的二叉树， 不失一般性

2 6.2 二叉树 为何要重点研究每结点最多只有两个 “叉” 的树？ ✓ 二叉树的结构最简单，规律性最强； ✓ 可以证明，所有树都能转为唯一对应的二叉树， 不失一般性。 6.2.1 二叉树的定义 6.2.2 二叉树的性质 6.2.3 二叉树的存储结构

6.2.2二叉树的性质 (3+2) 性质1：在二叉树的第层上至多有2-1个结点(>0)。 性质2： 深度为k的二叉树至多有2k1个结点(k>0) 性质3 对于任何一棵二叉树，若2度的结点数有2个，则叶 子数(no)必定为n2+1(即n,n2+1) 对于两种特殊形式的二叉树（满二叉树和完全二叉树） 还特别具备以下2个性质： 性质4：具有n个结点的完全二叉树的深度必为LIog2n」+1 性质5：对完全二叉树，若从上至下、从左至右编号，则 编号为的结点，其左孩子编号必为2，其右孩子编号为 2i+1:其双亲的编号必为2创(i=1时为根，除外)

3 6.2.2 二叉树的性质 (3+2) 性质1: 在二叉树的第i层上至多有2 i-1个结点（i>0）。 性质2: 深度为k的二叉树至多有2 k-1个结点（k>0）。 性质3: 对于任何一棵二叉树，若2度的结点数有n2个，则叶 子数（n0）必定为n2＋1 （即n0=n2+1） 对于两种特殊形式的二叉树（满二叉树和完全二叉树）， 还特别具备以下2个性质： 性质4: 具有n个结点的完全二叉树的深度必为log2n＋1 性质5: 对完全二叉树，若从上至下、从左至右编号，则 编号为i 的结点，其左孩子编号必为2i，其右孩子编号为 2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）

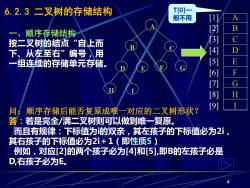
6.2.3二叉树的存储结构 T[O]一 般不用 B 一、 顺序存储结构 按二叉树的结点“自上而 下、从左至右”编号)用 一组连续的存储单元存储。 4567N9 问：顺序存储后能否复原成唯一对应的二叉树形状？ 答：若是完全/满二叉树侧可以做到唯一复原。 而且有规律：下标值为的双亲，其左孩子的下标值必为2ⅰ， 其右孩子的下标值必为2ⅰ+1（即性质5） 例如，对应[2]的两个孩子必为[4]和[5]，即B的左孩子必是 D,右孩子必为E

4 6.2.3 二叉树的存储结构 一、顺序存储结构 按二叉树的结点“自上而 下、从左至右”编号，用 一组连续的存储单元存储。 A B C D E F G H I [1] [2] [3] [4] [5] [6] [7] [8] [9] A B C E G I D H F 问：顺序存储后能否复原成唯一对应的二叉树形状？ 答：若是完全/满二叉树则可以做到唯一复原。 而且有规律：下标值为i的双亲，其左孩子的下标值必为2i， 其右孩子的下标值必为2i＋1（即性质5） 例如，对应[2]的两个孩子必为[4]和[5],即B的左孩子必是 D,右孩子必为E。 T[0]一 般不用

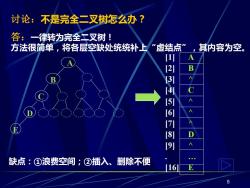
讨论：不是完全二叉树怎么办？ 答：一律转为完全二叉树！ 方法很简单，将各层空缺处统统补上“虚结点”，其内容为空。 四 23456789 缺点：①浪费空间；②插入、删除不便 6 5

5 讨论：不是完全二叉树怎么办？ 答：一律转为完全二叉树！ 方法很简单，将各层空缺处统统补上“虚结点” ，其内容为空。 A B ^ C ^ ^ ^ D ^ . E [1] [2] [3] [4] [5] [6] [7] [8] [9] . [16] A B E C D 缺点：①浪费空间；②插入、删除不便

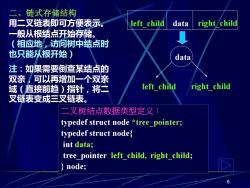
二、链式存储结构 用二叉链表即可方便表示。 left child data right/child 一般从根结点开始存储。 (相应地，访问树中结点时 也只能从根开始) data 注：如果需要倒查某结点的 双亲，可以再增加一个双亲 域（直接前趋）指针，将二 left child right child 叉链表变成三叉链表。 二叉树结点数据类型定义： typedef struct node *tree pointer; typedef struct node{ int data; tree pointer left child,right child; node; 6

6 二、链式存储结构 用二叉链表即可方便表示。 left_child data right_child data left_child right_child 二叉树结点数据类型定义： typedef struct node *tree_pointer; typedef struct node{ int data; tree_pointer left_child, right_child; } node; 一般从根结点开始存储。 （相应地，访问树中结点时 也只能从根开始） 注：如果需要倒查某结点的 双亲，可以再增加一个双亲 域（直接前趋）指针，将二 叉链表变成三叉链表

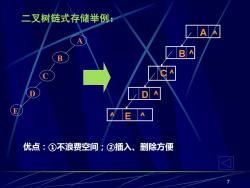
二叉树链式存储举例： B D EA 优点：①不浪费空间；②插入、删除方便

7 二叉树链式存储举例： A B E C D A ^ B ^ D C ^ ^ ^ E ^ 优点：①不浪费空间；②插入、删除方便

6.3遍历二叉树和线索二叉树 6.3.1遍历二叉树1 Traversing Binary Tree 遍历定义— 指按某条搜索路线遍访每个结点且不重复 (又称周游) 遍历用途 它是树结构插入、删除、修改、 查找和排序运 算的前提，是二叉树一切运算的基础和核心。 遍历方法 对每个结点的查看通常都是“先左后右

8 6.3 遍历二叉树和线索二叉树 6.3.1 遍历二叉树 遍历定义—— 遍历用途—— 遍历方法—— 指按某条搜索路线遍访每个结点且不重复 （又称周游）。 它是树结构插入、删除、修改、查找和排序运 算的前提，是二叉树一切运算的基础和核心。 对每个结点的查看通常都是“先左后右” 。 Traversing Binary Tree

遍历规则 二叉树由抽想 医子树佑子树构成，定义为D、L、R DL、 R的组合定义了六种可能的遍历方案 LDR,LRD,DLR,DRL RDD, RLD 若限定先左后右，则有三种实现方案： DLR LDR LRD 先序遍历 中序遍历 后序遍历 注：(“先、中、房”的意思是指访问的结点D是先于子树出 现还是后于子树出现。 以根结点为参照系 9

9 遍历规则——— ❖ 二叉树由根、左子树、右子树构成，定义为D、 L、R 以根结点为参照系 注：“先、中、后”的意思是指访问的结点D是先于子树出 现还是后于子树出现。 ❖ D、 L、R的组合定义了六种可能的遍历方案： LDR, LRD, DLR, DRL, RDL, RLD ❖ 若限定先左后右，则有三种实现方案： DLR LDR LRD 先序遍历 中序遍历 后序遍历

例1： 先序遍历的结果是： ABD EC 中序遍历的结果是：】 D BEAC 后序遍历的结果是：DEBCA 口诀： DLR一先序遍历，即先根再左再右 LDR一中序遍历，即先左再根再右 LRD一后序遍历，即先左再右再根 10

10 例1： 先序遍历的结果是： 中序遍历的结果是： 后序遍历的结果是： A B C D E D B E A C D E B C A 口诀： DLR—先序遍历，即先根再左再右 LDR—中序遍历，即先左再根再右 LRD—后序遍历，即先左再右再根 A B D E C