《数据结构》课程PPT教学课件（2015）第7章 图（下）

《数据结构》 第七章图下)

《 数据结构》 第七章 图 (下)

数据结构 第七章 7.1图的定义和术语 7.2图的存储结构 7.2.1数组表示法 7.2.2邻接表 7.3图的遍历 7.3.1深度优先搜索 7.3.2广度优先搜索 7.4图的连通性问题 7.4.3最小生成树 7.5有向无环图及其应用 7.5.1拓扑排序 7.6最短路径 7.6.1从某个源点到其余各顶点的最短路径 7.6.2每一对顶点之间的最短路径 tjm

数据结构 tjm 第七章 图 7.1 图的定义和术语 7.2 图的存储结构 7.2.1 数组表示法 7.2.2 邻接表 7.3 图的遍历 7.3.1 深度优先搜索 7.3.2 广度优先搜索 7.4 图的连通性问题 7.4.3 最小生成树 7.5 有向无环图及其应用 7.5.1 拓扑排序 7.6 最短路径 7.6.1 从某个源点到其余各顶点的最短路径 7.6.2 每一对顶点之间的最短路径

数据结构 7.3图的遍历 7.3.1深度优先搜索 方法：从图的某一顶点V0出发，访问此顶点： 然后依次从V0的未被访问的邻接点出发，深度 优先遍历图，直至图中所有和V0相通的顶点都 被访问到； 若此时图中尚有顶点未被访问，则另选图中一个 未被访问的顶点作起点，重复上述过程，直至图 中所有顶点都被访问为止

数据结构 tjm 7.3 图的遍历 7.3.1 深度优先搜索 方法：从图的某一顶点V0出发，访问此顶点； 然后依次从V0的未被访问的邻接点出发，深度 优先遍历图，直至图中所有和V0相通的顶点都 被访问到； 若此时图中尚有顶点未被访问，则另选图中一个 未被访问的顶点作起点,重复上述过程，直至图 中所有顶点都被访问为止

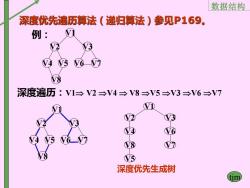
数据结构 深度优先遍历算法（递归算法）参见P169。 例： 45 V8 深度遍历：V1→V2→V4→V8→V5→V3→V6→V7 V2 V3 4 6 8 D 5 深度优先生成树

数据结构 tjm V1 V2 V4 V5 V3 V6 V7 V8 例： 深度遍历：V1 V2 V4  V8 V5 V3 V6 V7 深度优先遍历算法（递归算法）参见P169。 V1 V2 V4 V5 V3 V7 V6 V8 深度优先生成树 V1 V2 V4 V5 V3 V6 V7 V8

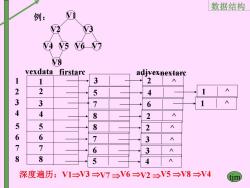
数据结构 例： 9§N67 v8 vexdata firstarc adivexnextarc 1 3 2 2 2 4 3 3 6 4 4 8 2 5 5 8 2 6 6 1 3 7 7 6 3 8 8 5 深度遍历：V1→V3→V7台V6→V2→V5→V8→V4

数据结构 tjm V1 V2 V4 V5 V3 V6 V7 V8 例： 1 2 3 4 1 3 4 2 vexdata firstarc 2 7 8 3 ^ ^ ^ adjvexnextarc 5 5 6 5 4 1 ^ 1 2 8 2 ^ 6 7 8 6 7 8 7 3 6 3 5 4 ^ ^ ^ 深度遍历：V1V3 V7 V6 V2 V5 V8 V4

数据结构 7.3.2广度优先搜索 方法：从图的某一顶点V0出发，访问此顶点后， 依次访问V0的各个未曾访问过的邻接点；然后 分别从这些邻接点出发，广度优先遍历图，直 至图中所有已被访问的顶点的邻接点都被访问 到： 若此时图中尚有顶点未被访问，则另选图中一 个未被访问的顶点作起点，重复上述过程，直 至图中所有顶点都被访问为止

数据结构 tjm 7.3.2 广度优先搜索 方法：从图的某一顶点V0出发，访问此顶点后， 依次访问V0的各个未曾访问过的邻接点；然后 分别从这些邻接点出发，广度优先遍历图，直 至图中所有已被访问的顶点的邻接点都被访问 到； 若此时图中尚有顶点未被访问，则另选图中一 个未被访问的顶点作起点，重复上述过程，直 至图中所有顶点都被访问为止

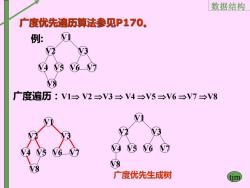
数据结构 广度优先遍历算法参见P170。 例： i 2 V3 W45W67 V8 广度遍历：V1→V2→V3→V4→V5→V6→V7→V8 3 W45W67 ⑧8 广度优先生成树 m

数据结构 tjm V1 V2 V4 V5 V3 V6 V7 V8 例: 广度遍历：V1 V2 V3  V4 V5 V6 V7 V8 广度优先遍历算法参见P170。 V1 V2 V4 V5 V3 V6 V7 V8 广度优先生成树 V1 V2 V4 V5 V3 V6 V7 V8

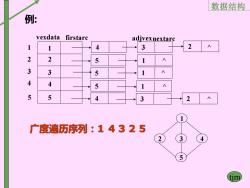
数据结构 例： vexdata firstarc adivexnextarc 4 3 2 2 2 5 A 3 3 5 4 4 5 5 5 2 广度遍历序列：14325 5 tim

数据结构 tjm 例: 1 2 3 4 5 1 2 3 4 1 3 4 2 vexdata firstarc 5 5 4 3 ^ ^ ^ adjvexnextarc 5 5 5 1 ^ 1 1 4 3 ^ 2 2 广度遍历序列：1 4 3 2 5

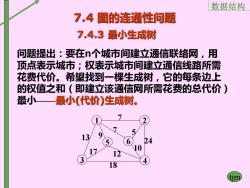
数据结构 7.4图的连通性问题 7.4.3最小生成树 问题提出：要在个城市间建立通信联络网，用 顶点表示城市；权表示城市间建立通信线路所需 花费代价。希望找到一棵生成树，它的每条边上 的权值之和（即建立该通信网所需花费的总代价） 最小一最小（代价）生成树。 18

数据结构 tjm 7.4 图的连通性问题 问题提出：要在n个城市间建立通信联络网，用 顶点表示城市；权表示城市间建立通信线路所需 花费代价。希望找到一棵生成树，它的每条边上 的权值之和（即建立该通信网所需花费的总代价） 最小——最小(代价)生成树。 1 5 6 3 4 2 7 13 17 9 18 12 7 5 24 10 7.4.3 最小生成树

数据结构 构造最小生成树的方法 方法一：普里姆(Prim)算法 算法思想：设N=(V,{E)是连通网，TE是N上 最小生成树中边的集合。 初始令U={u0,(u0e),TE=Φ。 在所有u∈U,veV-U的边(u,v)eE中，找一条代 价最小的边(u0,v0)。 将(u0,V0)并入集合TE,同时v0并入U。 重复上述操作直至U=V为止，则T=(,{TE}) 为N的最小生成树。 m

数据结构 tjm 算法思想：设N=(V,{E})是连通网，TE是N上 最小生成树中边的集合。 初始令U={u0},(u0V), TE=。 在所有uU,vV-U的边(u,v)E中，找一条代 价最小的边(u0,v0)。 将(u0,v0)并入集合TE，同时v0并入U。 重复上述操作直至U=V为止，则T=(V,{TE}) 为N的最小生成树。 方法一：普里姆(Prim)算法 构造最小生成树的方法