《数据结构》课程PPT教学课件（2012）第6章 树和二叉树 Tree & Binary Tree（4/4）

第二次上机内容预告： （三个方案由易到难，可自选，参见自测题集实验二资料) 方案一：二叉树的建立和遍历 具体内容：先生成一棵二叉树，再用中序遍历方式打印每个 结点值，并统计其叶子结点的个数。 方案二：哈夫曼树的建立和编码器的实现 具体内容：先生成一棵哈夫曼树，再打印各字符对应的哈夫 曼编码。 方案三：哈夫曼编/译码器的设计与实现

1 方案一：二叉树的建立和遍历 具体内容：先生成一棵二叉树，再用中序遍历方式打印每个 结点值，并统计其叶子结点的个数。 方案二：哈夫曼树的建立和编码器的实现 具体内容：先生成一棵哈夫曼树，再打印各字符对应的哈夫 曼编码。 方案三：哈夫曼编/译码器的设计与实现 第二次上机内容预告： （三个方案由易到难，可自选，参见自测题集实验二资料）

第6章树和二叉树 CTree Binary Tree) 6.1树的基本概念 6.2 二叉树 6.3 遍历二叉树和线索二叉树 6.4 树和森林 6.5 Huffman树及其应用 2

2 第6章 树和二叉树 （Tree & Binary Tree） 6.1 树的基本概念 6.2 二叉树 6.3 遍历二叉树和线索二叉树 6.4 树和森林 6.5 Huffman树及其应用

先介绍二叉树的典型应用 平衡树 特点：所有结点左右子树深度差s1 排序树 特点：所有结点“左小右大” 字典树 由字符串构成的二叉排序树 判定树 特点：分支查找树（例如12个球如何只称3次 便分出轻重) 带权树 特点：路径带权值（例如长度） 最优树 是带权路径长度最短的树，又称Huffman树， 用途之一是通信中的压缩编码。 3

3 先介绍二叉树的典型应用 平衡树—— 排序树—— 字典树—— 判定树—— 带权树—— 最优树—— 由字符串构成的二叉排序树 特点：分支查找树（例如12个球如何只称3次 便分出轻重） 特点：路径带权值（例如长度） 是带权路径长度最短的树，又称 Huffman树， 用途之一是通信中的压缩编码。 特点：所有结点左右子树深度差≤1 特点：所有结点“左小右大

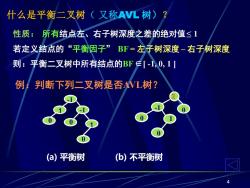
什么是平衡二叉树（又称AVL树） 性质：所有结点左、右子树深度之差的绝对值≤1 若定义结点的“平衡因子”BF=左子树深度-右子树深度 则：平衡二叉树中所有结点的BF∈[-1,0,1] 例 判断下列二叉树是否AVL树？ (a)平衡树 (b)不平衡树

4 什么是平衡二叉树（ 又称AVL 树）？ 性质： 所有结点左、右子树深度之差的绝对值≤ 1 若定义结点的“平衡因子” BF = 左子树深度 – 右子树深度 则：平衡二叉树中所有结点的BF∈[ -1, 0, 1 ] (a) 平衡树 (b) 不平衡树 例：判断下列二叉树是否AVL树？ 0 0 0 1 1 -1 -1 2 0 0 0 1 -1

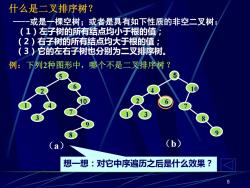
什么是二叉排序树？ 一一一或是一棵空树；或者是具有如下性质的非空二叉树： （1)左子树的所有结点均小于根的值： (2)右子树的所有结点均大于根的值： (3)它的左右子树也分别为二叉排序树。 例：下列2种图形中，哪个不是二叉排序树？ (a (b) 想一想：对它中序遍历之后是什么效果？

5 什么是二叉排序树？ （a） （b） 例：下列2种图形中，哪个不是二叉排序树？ -或是一棵空树；或者是具有如下性质的非空二叉树： （1）左子树的所有结点均小于根的值； （2）右子树的所有结点均大于根的值； （3）它的左右子树也分别为二叉排序树。 想一想：对它中序遍历之后是什么效果？ 7 1 4 10 2 6 5 3 9 8 5 10 2 1 6 4 7 3 9 8

什么是判定树？ 举例： 12个球如何用天平只称3次便分出轻重？ 分析： 12个球中必有一个非轻即重，即共有24种“次品”的可能性。 每次天平称重的结果有3种，连称3次应该得到的结果有33=27 说明仅用3次就能找出次品的可能性是存在的。 思路： 首先，将12个球分三组，每组4个，任意取两组称。会有两种情 况：平衡，或不平衡。 其次，一定要利用已经称过的那些结论；即充分利用“旧球”的 标准性作为参考。 6

6 什么是判定树？ 举例： 12个球如何用天平只称3次便分出轻重？ 分析： 12个球中必有一个非轻即重，即共有24种“次品”的可能性。 每次天平称重的结果有3种，连称3次应该得到的结果有3 3=27 种。 说明仅用3次就能找出次品的可能性是存在的。 思路： 首先，将12个球分三组，每组4个，任意取两组称。会有两种情 况：平衡，或不平衡。 其次，一定要利用已经称过的那些结论；即充分利用“旧球”的 标准性作为参考

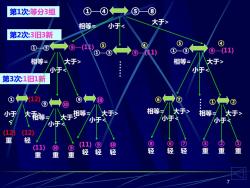
第1次：等分3组 ④ ⑤⑧ 相等 小于 大于> 第2次：3旧3新 ⑤ ④ ⑤ ④ ①③ ⑨-(11) ①® ⑨ 11 ①® ⑨(11) 相等= 大于> 相等= 大于> 小杆 小< 第3次：1旧1新 ① 12 ⑥ ⑦ ① 小 相等 大于相等 大于 相等 于 相等 小年 (12) (12) 重 轻 (11)⑨ ⑧ (6 ⑦ ② 11) ⑨ 轻 轻 轻 轻 轻 轻 重 重 重 重 重

7 第1次:等分3组 第2次:3旧3新 第3次:1旧1新 ①—④ ⑤—⑧ 相等= 小于 ①—③ ⑨—(11) 相等= 大于> 小于 小于 小于 (12) 轻 ⑨ ⑩ 大于> 小于 小于 小于< 相等= ③ 重 ① 重 ② 重

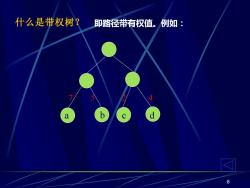
什么是带权树？ 即路径带有权值。例如： 4 a 8

8 什么是带权树？ a b c d 7 5 2 4 即路径带有权值。例如：

6.5 Huffman树及其应用 Huffman?树 二、Huffman编码 带权路径 长度最短 的树 Huffman树 最优二叉树 是通信 Huffman编码 不等长编码 中最经 典的压 缩编码 9

9 6.5 Huffman树及其应用 一、Huffman树 二、Huffman编码 Huffman树 最优二叉树 Huffman编码 带权路径 长度最短 的树 不等长编码 是通信 中最经 典的压 缩编码

一、 Huffman树（最优三叉树） 若干术语 路 径：由一结点到另一结点间的分支所构成。 路径长度：路径上的分支数目。例如：a大e的路径长度=2 树的路径长度：从树根到每一结点的路径长度之和。树长度=10 带权路径长度：结点到根的路径长度与结点上权的乘积(WPL) Weighted Path 树的带权路径长度：即树中所有解点的带权路径长度之和 Huffman树：带权路径长度最小的树。 Huffman常译为赫夫曼、霍夫鼻、哈夫曼等 10

10 一、 Huffman树（最优二叉树） 路 径： 路径长度： 树的路径长度： 带权路径长度： 树的带权路径长度： Huffman树： 由一结点到另一结点间的分支所构成。 路径上的分支数目。 从树根到每一结点的路径长度之和。 结点到根的路径长度与结点上权的乘积（WPL） 若干术语： d e b a c f g 即树中所有叶子结点的带权路径长度之和 带权路径长度最小的树。 例如：a→e的路径长度＝ 树长度＝ 2 10 Huffman常译为赫夫曼、霍夫曼、哈夫曼等 Weighted Path Length