《数据结构》课程PPT教学课件（2012）第7章 图（3/3）

第7章1 图 7.1基本术语 7.2存储结构 7.3图的遍历 7.4图的其他运算 7.5图的应用

1 7.1 基本术语 7.2 存储结构 7.3 图的遍历 7.4 图的其他运算 7.5 图的应用 第7章 图

7.4图的其他运算 1.求图的生成树 2.求最小生成树 3.求最短路径 4.求关节点和重连通分量（略） 5.拓扑排序（见下节) 6.求关键路径（见下节) 2

2 7.4 图的其他运算 1. 求图的生成树 2. 求最小生成树 3. 求最短路径 4. 求关节点和重连通分量（略） 5. 拓扑排序（见下节） 6. 求关键路径（见下节）

1.求图的生成树（小结） 生成树的特征： n个顶点的连通图的生成树有n个 顶点、n-1条边。 求生成树的方法： DFS（深度优先搜索 ) BFS(广度优先搜索 ) 注1：生成树是原图的极小连通子图： 注2：从不同顶点出发进行DFS或BFS,得到的 生成树不同，即：图的生成树不惟一

3 1. 求图的生成树（小结） 生成树的特征: ——n 个顶点的连通图的生成树有 n 个 顶点、n-1 条边。 求生成树的方法: ——DFS（深度优先搜索） ——BFS（广度优先搜索） 注1：生成树是原图的极小连通子图； 注2：从不同顶点出发进行DFS或BFS，得到的 生成树不同，即：图的生成树不惟一

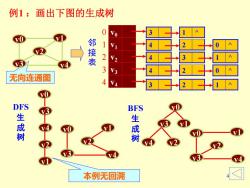
例1：画出下图的生成树 2 邻接表 2 3 3 无向连通图 4 DFS BFS 生成树 生成树 本例无回溯

4 例1 ：画出下图的生成树 DFS 生 成 树 v0 v1 v2 v43 v4 邻 接 表 0 1 2 3 4 3 1 ^ 4 3 1 ^ 4 2 0 ^ v4 v3 v2 v1 v0 3 2 1 ^ 4 2 0 ^ v0 v2 v1 v4 v3 BFS 生 成 树 v0 v3 v1 v4 v2 无向连通图 v0 v1 v2 v43 v4 v0 v1 v2 v43 v4 本例无回溯

2. 求最小生成树 Minimum Cost Spanning Tree 目标：在网（有权图）的多个生成树中、寻找一 个各边权值之和最小的生成树(MST)。 注：任何一个无向连通图的最小生成树只有一棵。 典型实例：n个城市建网，如何选择-I条线路，使总费用 最少？一 用最小生成树求解 求最小生成树有两种方法： 对边操作 Kruskal(克鲁斯卡尔)算法 Prim（普里姆)算法 对顶点操作

5 Minimum Cost Spanning Tree 2. 求最小生成树 目标：在网（有权图）的多个生成树中，寻找一 个各边权值之和最小的生成树（MST）。 典型实例： n个城市建网，如何选择n–1条线路，使总费用 最少？——用最小生成树求解 ❖ Kruskal（克鲁斯卡尔）算法 ❖ Prim（普里姆）算法 求最小生成树有两种方法： 注：任何一个无向连通图的最小生成树只有一棵。 对边操作 对顶点操作

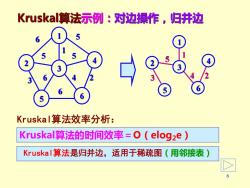
Kruskal算法示例：对边操作，归并边 Kruska l:算法效率分析： Kruskal算法的时间效率=O（elog2e) Kruskal算法是归并边，适用于稀疏图（用邻接表）

6 Kruskal算法示例：对边操作，归并边 1 4 6 5 2 3 1 5 6 5 5 6 4 3 6 2 1 5 4 3 2 1 3 5 2 4 6 Kruskal算法效率分析： Kruskal算法的时间效率＝O（elog2e） Kruskal算法是归并边，适用于稀疏图（用邻接表）

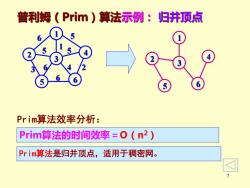
普利姆(Prim)算法示例：归并顶点 Prim算法效率分析： Prim算法的时间效率=O(n2) Prim算法是归并顶点，适用于稠密网

7 普利姆（Prim）算法示例： 归并顶点 1 4 5 6 2 3 1 6 5 5 5 3 6 4 6 2 3 6 4 2 5 1 Prim算法效率分析： Prim算法的时间效率＝O（n2） Prim算法是归并顶点，适用于稠密网

3.求最短路径 典型用途：交通问题。如：城市A到城市B有多条线路，但每 条线路的交通费（或所需时间)不同，那么，如何选择一条线 路，使总费用（或总时间）最少？ 问题抽象：在带权有向图中A点（源点）到达B点（终点）的 多条路径中，寻找一条各边权值之和最小的路径，即最短路径。 (注：最短路径与最小生成树不同，路径上不一定包含个顶点) 两种常见的最短路径问题： 单源最短路径一用Dijkstra(迪杰斯特拉)算法 二、 所有顶点间的最短路径一用loyd(弗洛伊德)算法 任意两顶 一顶点到其 点之间 余各顶点

8 一顶点到其 余各顶点 3. 求最短路径 两种常见的最短路径问题： 一、 单源最短路径—用Dijkstra（迪杰斯特拉）算法 二、所有顶点间的最短路径—用Floyd（弗洛伊德）算法 典型用途：交通问题。如：城市A到城市B有多条线路，但每 条线路的交通费（或所需时间）不同，那么，如何选择一条线 路，使总费用（或总时间）最少？ 问题抽象：在带权有向图中A点（源点）到达B点（终点）的 多条路径中，寻找一条各边权值之和最小的路径，即最短路径。 （注：最短路径与最小生成树不同，路径上不一定包含n个顶点） 任意两顶 点之间

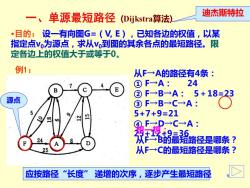
一、单源最短路径(Dijkstra算法) 迪杰斯特拉 ·目的：设一有向图G=(V,E),已知各边的权值，以某 指定点Vo为源点，求从Vo到图的其余各点的最短路径。限 定各边上的权值大于或等于0。 例1： 从F→A的路径有4条： ①F→A:24 B ②F→B→A:5+18=23 源点 ③F→B→C→A: 5 5+7+9=21 0 24 帮条是隆？ D 25 从F→C的最短路径是哪条？ 应按路径“长度”递增的次序，逐步产生最短路径

9 一、单源最短路径 (Dijkstra算法) •目的： 设一有向图G=（V, E），已知各边的权值，以某 指定点v0为源点，求从v0到图的其余各点的最短路径。限 定各边上的权值大于或等于0。 例1： 源点 从F→A的路径有4条： ① F→A： 24 ② F→B→A： 5＋18=23 ③ F→B→C→A： 5+7+9=21 ④ F→D→C→A： 25+12+9=36 想一想： 从F→B的最短路径是哪条？ 从F→C的最短路径是哪条？ 迪杰斯特拉 应按路径“长度” 递增的次序，逐步产生最短路径

二、所有顶点之间的最短路径 可以通过调用n次Dijkstra算法来完成， 时间复杂度为0(n3) 还有更简单的一个算法：Floyd?算法 （略) 回 0

10 二、所有顶点之间的最短路径 可以通过调用n次Dijkstra算法来完成， 时间复杂度为O(n3) 还有更简单的一个算法：Floyd算法（略）