《数据结构》课程PPT教学课件（2012）第3章 栈和队列 3.1 栈（Stack）

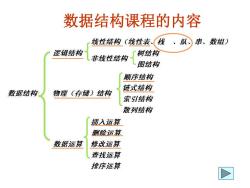
数据结构课程的内容 线性结构（线性表（找、队） 串、数组) 逻辑结构 树结构 非线性结构 图结构 颜序结构 链式结构 数据结构： 物理（存储)结构 索引结构 散列结构 插入运算 删除运算 数据运算 修改运算 查找运算 排序运算 D

数据结构课程的内容

第三章栈和队列 3.1 栈(Stack) 3.2X队列(Queue) 1. 定义 1.定义 2.逻辑结构 2.逻辑结构 3.存储结构 3.存储结构 4.运算规则 4.运算规则 5。实现方式 5.实现方式

2 3.1 栈（Stack） 3.2 队列（Queue） 第三章 栈和队列 1. 定义 2. 逻辑结构 3. 存储结构 4. 运算规则 5. 实现方式 1. 定义 2. 逻辑结构 3. 存储结构 4. 运算规则 5. 实现方式

3.1栈 即栈顶 1.定义 限定只能在表的一端进行插入和删除运算的 线性表。 2.逻辑结构 与线性表相同，仍为一对一(1：1)关系。 3.存储结构 用顺序栈或链栈存储均可，但以顺序栈更常见 4.运算规则 只能在栈顶运算，且访问结点时依照后进先出 (LIFO)或先进后出(FIL0)的原则。 5.实现方式 关键是编写入栈和出栈函数，具体实现依顺 序栈或链栈的存储结构有别而不同。 基本操作有： 建栈、判断栈满或栈空、入栈、出栈、 读栈顶元素值，等等

3 1. 定义 与线性表相同，仍为一对一( 1:1)关系。 用 或 存储均可，但以顺序栈更常见 只能在 运算，且访问结点时依照 （LIFO）或 （FILO）的原则。 关键是编写 和 函数，具体实现依顺 序栈或链栈的存储结构有别而不同。 3. 存储结构 4. 运算规则 5. 实现方式 2. 逻辑结构 限定只能在表的 进行插入和删除运算的 线性表。 即栈顶 基本操作有：建栈、判断栈满或栈空、入栈、出栈、 读栈顶元素值，等等

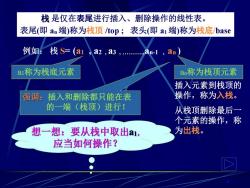
栈是仅在表尾进行插入、删除操作的线性表。 表尾（即an端）称为栈顶/top;表头（即a1端）称为栈底/base 例如： 栈S=(a1 a2,a3,.an-1,an a1称为栈底元素 an称为栈顶元素 插入元素到栈顶的 强调：插入和删除都只能在表 操作，称为入栈。 的一端（栈顶）进行！ 从栈顶删除最后一 个元素的操作，称 想一想：要从栈中取出a1, 为出栈。 应当如何操作？

4 是仅在表尾进行插入、删除操作的线性表。 表尾(即 an端)称为栈顶 /top ; 表头(即 a1端)称为栈底/base 例如： 栈 = (a1 , a2 , a3 , .,an-1 , an ) 插入元素到栈顶的 操作，称为入栈。 从栈顶删除最后一 个元素的操作，称 为出栈。 a1称为栈底元素 an称为栈顶元素 插入和删除都只能在表 的一端（栈顶）进行！

Q1:堆栈是什么？它与一般线性表有什么不同？ 堆栈是一种特殊的线性表，它只能在表的一端（即 栈顶)进行插入和删除运算。 与一般线性表的区别：仅在于运算规则不同。 般线性表 堆栈 逻辑结构：1：1 逻辑结构： 1:1 存储结构：顺序表、链表 存储结构：顺序栈、链栈 运算规则：随机存取 运算规则： 后进先⊕LFO “进”=插入=压入=PUSH(anti） “出”=删除=弹出=POP(an)

5 Q1：堆栈是什么？它与一般线性表有什么不同？ 堆栈是一种特殊的线性表，它只能在表的一端（即 栈顶）进行插入和删除运算。 与一般线性表的区别：仅在于 不同。 逻辑结构：1:1 逻辑结构： 1:1 存储结构：顺序表、链表 存储结构：顺序栈、链栈 运算规则： 运算规则： (LIFO) “进”＝插入=压入=PUSH（an+1) “出”＝删除=弹出=POP(an)

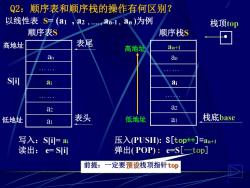
Q2:顺序表和顺序栈的操作有何区别？ 以线性表S(a,a2,an-1,an)为例 栈顶top 顺序表S 顺序栈S 高地址 表尾 高地址 an+1 an an · S ai ai 。.， a2 a2 低地址 a 表头 低地址 ai 栈底base 写入：S=ai 压入PUSD:S[topt+]=an+1 读出：e=S] 弹出(POP):e=S[-二top] 前提：一定要预设栈顶指针top

6 a1 a2 . an 顺序栈S ai . Q2：顺序表和顺序栈的操作有何区别？ 表头 表尾 低地址 高地址 写入：S[i]= ai 读出： e= S[i] 压入( S[ ++]=an+1 弹出( [- ] 低地址 高地址 S[i] a1 a2 ai an . 顺序表S . an+1 以线性表 S= (a1 , a2 , . , an-1 , an )为例 栈底 栈顶 前提：一定要 栈顶指针 栈顶

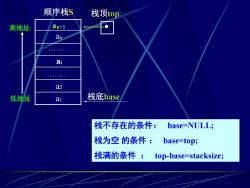
顺序栈S 栈顶top 高地址 an+1 an ai a2 低地址 ai 栈底base 栈不存在的条件： base=NULL; 栈为空的条件：base=top; 栈满的条件：top-base=stacksize;

7 栈不存在的条件： base=NULL; 栈为空 的条件 ： base=top; 栈满的条件 ： top-base=stacksize; a1 a2 . an 顺序栈S ai . 低地址 高地址 an+1 栈底 栈顶

Q3:什么叫“向上生成”的栈？“向下生成”又是何 意？ 若入栈动作使地址向高端增长，称为“向上生成”的栈； 若入栈动作使地址向低端增长，称为《向下生成”的栈； 对于向上生成的堆栈： 入栈口诀：堆栈指针top“先压后加”：S[top+]=ant1 出栈口诀：堆栈指针top“先减后弹”：e=S[top]

8 若入栈动作使地址向高端增长，称为“向上生成”的栈； 若入栈动作使地址向低端增长，称为“向下生成”的栈； 对于向上生成的堆栈: 入栈口诀：堆栈指针top “先压后加” : S[top++]=an+1 出栈口诀：堆栈指针top “先减后弹” : e=S[-top] Q3：什么叫“向上生成”的栈？ “向下生成”又是何 意？

Q4:为什么要设计堆栈？它有什么独特用途？ 调用函数或子程序非它莫属； 2. 递归运算的有力工具； 3.用于保护现场和恢复现场： 4.简化了程序设计的问题。 下面用4个例子来帮助理解堆栈：

9 Q4：为什么要设计堆栈？它有什么独特用途？ 1. 调用函数或子程序非它莫属； 2. 递归运算的有力工具； 3. 用于保护现场和恢复现场； 4. 简化了程序设计的问题。 下面用4个例子来帮助理解堆栈：

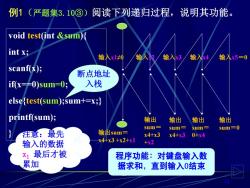
例1（严题集3.10③）阅读下列递归过程，说明其功能。 void test(int &sum) int x; 输入x10 输入权/输入3/输入4 输入x5=0 scanf(x); 断点地址 if(x=≠0)sum=0; 入栈 elseftest(sum);sum+=x;} printf(sum); 输出 输出 输出 输出 sum= 输出sum三 sum= sum= sum=0 注意：最先 x4+x3 x4+x30+x4 输入的数据 x4+x3+x2+x1 +x2 x1最后才被 程序功能：对键盘输入数 累加 据求和，直到输入0结束

10 void test(int &sum){ int x; scanf(x); if(x==0)sum=0; else{ ;sum+=x;} printf(sum); } 断点地址 入栈 例1（严题集3.10③）阅读下列递归过程，说明其功能。 输入x1≠0 输入x2 输入x3 输入x4 输入x5＝0 输出 sum＝0 输出 sum＝ 0+x4 输出 sum＝ x4+x3 输出 sum＝ x4+x3 +x2 输出sum＝ x4+x3 +x2+x1 注意：最先 输入的数据 x1 最后才被 累加 程序功能：对键盘输入数 据求和，直到输入0结束