《数据结构》课程PPT教学课件（2012）第3章 栈和队列 3.2 队列（Queue）

第三章栈和队列 3.1 栈 (Stack) 3.2 队列 (Queue) 1, 定义 1.定义 2.逻辑结构 2.逻辑结构 3.存储结构 3.存储结构 4.运算规则 4.运算规则 5.实现方式 5.实现方式

1 3.1 栈（Stack） 第三章 栈和队列 3.2 队列（Queue） 1. 定义 2. 逻辑结构 3. 存储结构 4. 运算规则 5. 实现方式 1. 定义 2. 逻辑结构 3. 存储结构 4. 运算规则 5. 实现方式

32队列 尾部插 队列定义 只能在表的一端进行插入运算， 在表的另一 端进行删除运算的线性表。 首部删 逻辑结构 与线性表相同，仍为一对一关系。 存储结构 顺序队或链队， 以循环顺序队更常见。 运算规则 只能在队首和队尾运算，且访问结点时依照 先进先出(FIFO)的原则。 实现方式 关键是掌握入队和出队操作，具体实现依顺 序队或链队的不同而不同。 基本操作：入队或出队，建空队列，判队空或队满等操作

2 与线性表相同，仍为一对一关系。 顺序队或链队，以循环顺序队更常见。 只能在队首和队尾运算，且访问结点时依照 先进先出（FIFO）的原则。 关键是掌握入队和出队操作，具体实现依顺 序队或链队的不同而不同。 只能在表的一端进行插入运算，在表的另一 端进行删除运算的线性表。 基本操作：入队或出队，建空队列，判队空或队满等操作。 尾部插 入 首部删 除

队列(Queue)是仅在表尾进行插入操作，在表头进行删除操 作的线性表。它是一种先进先出(FIFO)的线性表。 例如： 队列Q=(aa2,a3,an以， an 队首 队尾 在队尾插入元素称为入队；在队首删除元素称为出队。 问：为什么要设计队列？它有什么独特用途？ 答：1.离散事件的模拟（模拟事件发生的先后顺序，例如 CPU芯片中的指令译码队列)； 2.操作系统中的作业调度（二个CPU执行多个作业）； 3.简化程序设计

3 队列 （Queue）是仅在表尾进行插入操作，在表头进行删除操 作的线性表。它是一种先进先出（ＦＩＦＯ）的线性表。 例如：队列 Q= (a1 , a2 , a3 , .,an-1 , an ) 在队尾插入元素称为 ；在队首删除元素称为 。 队首 队尾 问：为什么要设计队列？它有什么独特用途？ 1. 离散事件的模拟（模拟事件发生的先后顺序,例如 CPU芯片中的指令译码队列）； 2. 操作系统中的作业调度（一个CPU执行多个作业）； 3. 简化程序设计。 答：

队的实现方式是本节重点，关键是掌握入队和出队操作。 具体实现依存储结构（链队或顺序队）的不同而不同。 1.链队列 2.顺序队 重点是循环 顺序队 队的抽象数据类型定义： ADT Queue{ 数据对象： D=, 建队、入队或出队、判队空 数据关系： R=. 或队满等，教材P59-60罗列 基本操作： 了9种基本操作。 0。e0 ADT Queue

4 关键是掌握入队和出队操作。 具体实现依存储结构（链队或顺序队）的不同而不同。 2. 队的抽象数据类型定义： ADT Queue{ 数据对象：D=. 数据关系：R=. 基本操作： . } ADT Queue 建队、入队或出队、判队空 或队满等，教材P59-60罗列 了9种基本操作。 重点是循环 顺序队

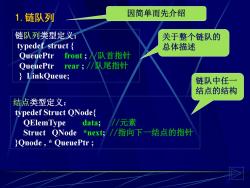
1.链队列 因简单而先介绍 链队列类型定义： 关于整个链队的 typedef struct 总体描述 QueuePtr front;W队首指针 QueuePtr rear;/队尾指针 }LinkQueue; 链队中任一 结点的结构 结点类型定义： typedef Struct QNode{ QElemType data; //元素 Struct QNode*next;/指向下一结点的指针 }Qnode,QueuePtr

5 链队列类型定义： typedef struct { QueuePtr front ; //队首指针 QueuePtr rear ; //队尾指针 } LinkQueue; 结点类型定义： typedef Struct QNode{ QElemType data; //元素 Struct QNode *next; //指向下一结点的指针 }Qnode , * QueuePtr ; 关于整个链队的 总体描述 链队中任一 结点的结构 因简单而先介绍

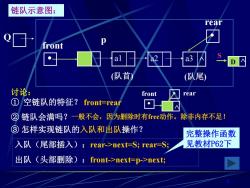
链队示意图： rear front al 2日 a3 (队首) (队尾) 讨论： front rear ①空链队的特征？front=rear ②链队会满吗？一般不会，因为删除时有free动作。除非内存不足！ ③怎样实现链队的入队和出队操作？ 完整操作函数 入队（尾部插入）：rear->next-S;rear=S; 见教材P62下 出队（头部删除）：front->next=p->next;

6 讨论： ① 空链队的特征？ Q (队首) (队尾) front a1 a2 a3 ^ rear p front ^ rear ③ 怎样实现链队的入队和出队操作？ ② 链队会满吗？ front=rear 一般不会，因为删除时有free动作。除非内存不足！ 入队（尾部插入）：rear->next=S; rear=S; 出队（头部删除）：front->next=p->next; S D ^ 链队示意图： 完整操作函数 见教材P62下

2.顺序队 关于整个顺序 顺序队类型定义： 队的总体描述 #define QUEUE-MAXSIZE100/最大队列长度 typedef struct QElemType *base; //队列的基址 int front; /队首指针 int rear; //队尾指针 SqQueue 顺序队中每个结点的结构描述在此省略，是QElemType类型。 建队核心语句： q.base=(QElemType *)malloc(sizeof (QElemType OUEUE MAXSIZE): /川分配空间 采用动态分配空 间的形式

7 采用动态分配空 间的形式 顺序队类型定义： 建队核心语句： q . base=(QElemType *)malloc(sizeof (QElemType ） * QUEUE_MAXSIZE); //分配空间 关于整个顺序 队的总体描述 #define QUEUE-MAXSIZE 100 //最大队列长度 typedef struct { QElemType *base; //队列的基址 int front; //队首指针 int rear; //队尾指针 }SqQueue 顺序队中每个结点的结构描述在此省略，是QElemType类型

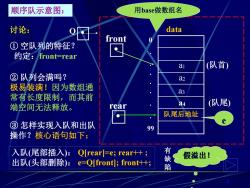
顺序队示意图： 用base做数组名 讨论： data front ①空队列的特征？ 约定：front=rear al (队首) ②队列会满吗？ a2 极易装满！因为数组通 a3 常有长度限制，而其前 端空间无法释放。 rear a4 (队尾) 队尾后地址 ③怎样实现入队和出队 99 操作？核心语句如下： 入队（尾部插入）：Q[rear=e;rear++; 有缺 假溢出！ 出队（头部删除）：e=Qfront];front+-+; 陷

8 Q (队尾) (队首) front a1 a2 a3 data a4 0 . . . . . . .99 rear ② 队列会满吗？ 极易装满！因为数组通 常有长度限制，而其前 端空间无法释放。 ① 空队列的特征？ 约定：front=rear 队尾后地址 入队(尾部插入)： Q[rear]=e; rear++ ; 出队(头部删除)： e=Q[front]; front++; 讨论： 有 缺 陷 ③ 怎样实现入队和出队 操作？核心语句如下： 用base做数组名 e 顺序队示意图：

问：什么叫“假溢出”？如何解决？ 答：在顺序队中，当尾指针已经到了数组的 上界，不能再有入队操作，但其实数组中还 有空位置，这就叫“假溢出” 解决假溢出的途径 采用循环队列

9 解决假溢出的途径———采用循环队列 答：在顺序队中，当尾指针已经到了数组的 上界，不能再有入队操作，但其实数组中还 有空位置，这就叫“假溢出” 。 问：什么叫“假溢出” ？如何解决？

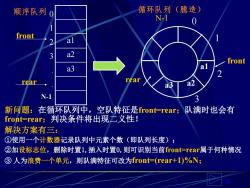
顺序队列0 循环队列（臆造） N1 0 front al 3 a2 front a3 al 2 rear→ rear a3 a2 N-1 新问题：在循环队列中，空队特征是front=rear; 队满时也会有 front-戶rear;判决条件将出现工义性！ 解决方案有三： ①使用一个计数器记录队列中元素个数（即队列长度）； ②加设标志位，删除时置1，插入时置0，则可识别当前front戶rear属于何种情况 ③人为浪费一个单元，则队满特征可改为front=-(rear+1)%N;

10 a3 a2 a1 0 1 2 3 N-1 rear front 新问题：在循环队列中，空队特征是front=rear；队满时也会有 front=rear；判决条件将出现二义性！ 解决方案有三： ①使用一个计数器记录队列中元素个数（即队列长度）； ②加设标志位，删除时置1,插入时置0,则可识别当前front=rear属于何种情况 ③ 人为浪费一个单元，则队满特征可改为front=(rear+1)%N； a3 a2 a1 front rear 0 1 2 3 . . N-1