《数据结构》课程PPT教学课件（2012）第10章 内部排序 10.5 归并排序 10.6 基数排序（Radix Sort）

第10章内邰排序 10.1概述 10.2插入排序 10.3交换排序 10.4选择排序 10.5归并排序 10.6基数排序 附：各种内部排序方法的比较

1 10.1 概述 10.2 插入排序 10.3 交换排序 10.4 选择排序 10.5 归并排序 10.6 基数排序 第10章 内部排序 附：各种内部排序方法的比较

10.5归并排序 归并排序的基本思想是：将两个（或以上)的有序 表组成新的有序表。 更实际的意义：可以把一个长度为n的无序序列看成是n个 长度为1的有序子序列，首先做两两归并，得到「n/21个 长度为2的有序子序列：再做两两归并，.，如此重复， 直到最后得到一个长度为的有序序列。 例：关键字序列T=（21,25,49,25*,93,62, 72,08,37,16,54),请给出归并排序的具体实 现过程

2 10.5 归并排序 归并排序的基本思想是：将两个（或以上）的有序 表组成新的有序表。 更实际的意义：可以把一个长度为n 的无序序列看成是 n 个 长度为 1 的有序子序列 ，首先做两两归并，得到 n / 2 个 长度为 2 的有序子序列 ；再做两两归并，.，如此重复， 直到最后得到一个长度为 n 的有序序列。 例：关键字序列T= （21，25，49，25* ，93，62， 72，08，37，16，54），请给出归并排序的具体实 现过程

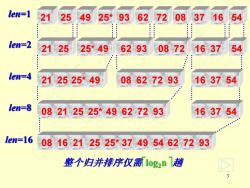
len=1 21 2549 25*93 62 72 08 37 16 54 len=2 2125 25*49 6293 0872 1637 len=4 212525*49 08627293 163754 len=8 08212525*49627293 163754 len=16 0816212525*374954627293 整个归并排序仅需10g2n1趟

3 21 25 49 25* 93 62 72 08 37 16 54 21 25 25* 49 62 93 08 72 16 37 54 16 37 54 21 25 25* 49 08 62 72 93 08 21 25 25* 49 62 72 93 08 16 21 25 25* 37 49 54 62 72 93 len=1 len=2 len=4 len=8 len=16 16 37 54 整个归并排序仅需log2n 趟

一趟归并排序算法：（两路有序并为一路） 参见救材P283 void Merge (SR,&TR,i,m,n) ∥将有序的SR[i.m和SRm+1.归并为有序的TR[i.n for(k=i,j=m+1;i<=m &&j<=n;++k){ if (SR[i]<=SR[j])TR[k]=SR[i++]; else TR[k=SR+;∥将两个SR记录由小到大并入TR }∥for f(=m)TRk.n=SRi.m;∥将剩余的SR[i.m复制到TR if(G=n)TRk.=SRj.n;∥将剩余的SRj.复制到TR }∥Merge 这就是能提高排 序速度的原因

4 一趟归并排序算法: (两路有序并为一路) 参见教材P283 void Merge (SR，&TR，i, m, n) { // 将有序的SR[i.m]和SR[m+1.n]归并为有序的TR[i.n] for(k=i , j=m+1; i<=m && j<=n; ++k ) { if ( SR[i]<= SR[j] )TR[k]=SR[i++]; else TR[k]=SR[j++]; // 将两个SR记录由小到大并入TR } // for if (i<=m) TR[k.n]=SR[i.m]; // 将剩余的SR[i.m]复制到TR if (j<=n) TR[k.n]=SR[j.n]; // 将剩余的SR[j.n]复制到TR } // Merge 这就是能提高排 序速度的原因

递归形式的两路归并完整排序算法： ：参见材P284 void MSort(SR[],&TR1】,s,){∠初次调用时为(L,L,l,length) /将无序的SRs.归并排序为TR1s. if(s=t)TR1s=SRs;∥当len=1时返▣ else m=(s+t)/2;∥将SR[s.t平分为SR[s.m和SR[m+1.) MSot(SR,&TR2,S,m);∥将SR一分为二，2分为4. /∥递归地将SRs.m归并为有序的TR2[s.m MSort (SR &TR2,m+1,t); ∥递归地将SR[m+1.归并为有序的TR2[m+1.) Merge(TR2,TR1,s,m,t); /将TR2[s.m和TR2m+1.t归并到TR1[s.t //if }I∥MSort 简言之，先由“长”无序变成“短”有序 再从“短”有序归并为“长”有序

5 if ( s==t )TR1[s]=SR[s]; // 当len=1时返回 else { } //if } // MSort m=(s+t)/2; // 将SR [s.t]平分为SR [s.m]和SR [m+1.t] MSort (SR，&TR2，s, m); // 将SR 一分为二, 2分为4. // 递归地将SR [s.m]归并为有序的TR2[s.m] MSort (SR，&TR2，m+1, t ); // 递归地将SR [m+1.t]归并为有序的TR2[m+1.t] Merge(TR2， TR1， s, m, t ); // 将TR2 [s.m]和TR2 [m+1.t]归并到TR1 [s.t] void MSort (SR[ ],&TR1[ ]，s, t) { // 将无序的SR[s.t]归并排序为TR1[s.t] 递归形式的两路归并完整排序算法: 参见教材P284 简言之，先由“长”无序变成“短”有序， 再从“短”有序归并为“长”有序。 初次调用时为（L, L, 1, length）

归并排序算法分析： 。时间效率：O(nlog2n) 因为在递归的归并排序算法中，函数Merge()做一趟两路归 并排序，需要调用merge()函数「n/(2lem)≈O(n/lem）次，而 每次merge()要执行t比较Olem)次，另外整个归并过程有 「log2n1“层”，所以算法总的时间复杂度为0(log2m)。 ● 空间效率：O(n) 因为需要一个与原始序列同样大小的辅助序列(T)。这 正是此算法的缺点。 。稳定性：稳定 6

6 归并排序算法分析： • 时间效率： O(nlog2n) 因为在递归的归并排序算法中，函数Merge( )做一趟两路归 并排序，需要调用merge ( )函数 n/(2len)  O(n/len) 次，而 每次merge( )要执行比较O(len)次，另外整个归并过程有 log2n “层” ，所以算法总的时间复杂度为O(nlog2n)。 • 空间效率： O(n) 因为需要一个与原始序列同样大小的辅助序列（TR）。这 正是此算法的缺点。 • 稳定性：稳定

10.6 基数排序 (Radix Sort) 基数排序的基本思想是： 借助多关键字排序的思想对单逻辑关键字进行排 序。即：用关键字不同的位值进行排序。 要时论的问题： 1.什么是“多关键字”排序？实现方法？ 2.单逻辑关键字怎样“按位值”排序？

7 10.6 基数排序 (Radix Sort) 要讨论的问题： 1. 什么是“多关键字”排序？实现方法？ 2. 单逻辑关键字怎样“按位值”排序？ 基数排序的基本思想是： 借助多关键字排序的思想对单逻辑关键字进行排 序。即：用关键字不同的位值进行排序

1.什么是“多关键字”排序？实现方法？ 例1：对一副扑克牌该如何排序？ 若规定花色和面值的顺序关系为： 花色：◆<品<v< 面值：2<3<4<5<6<7<8<9<10<J<Q<K<A 则可以先按花色排序，花色相同者再按面值排序； 也可以先按面值排序，面值相同者再按花色排序。 例2：职工分房该如何排序？ 我校规定：先以总分排序（职称分+工龄分)： 总分相同者，再按配偶总分排序，其次按配偶职称、 工龄、人口.等等排序。 以上两例都是典型的多关键字排序/

8 1. 什么是“多关键字”排序？实现方法？ 例1：对一副扑克牌该如何排序？ 若规定花色和面值的顺序关系为： 花色：        面值：2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < 10 < J < Q < K < A 则可以先按花色排序，花色相同者再按面值排序； 也可以先按面值排序，面值相同者再按花色排序。 例2：职工分房该如何排序？ 我校规定：先以总分排序（职称分＋工龄分）； 总分相同者，再按配偶总分排序，其次按配偶职称、 工龄、人口.等等排序。 以上两例都是典型的多关键字排序！

多关键字排序的实现方法通常有两种： 最高位优先法MSD(Most Significant Digit first) 最低位优先法LSD(Least Significant Digit first) 例：对一副扑克牌该如何排序？ 答：若规定花色为第一关键字（高位)，面值为第二关键字 （低位)，则使用MSD和LSD方法都可以达到排序目的。 MSD方法的思路：先设立4个花色“箱”，将全部牌按花色分 别归入4个箱内（每个箱中有13张牌)；然后对每个箱中的牌 按面值进行插入排序（或其它稳定算法)。 LSD方法的思路：先按面值分成13堆（每堆4张牌)，然后对 每堆中的牌按花色进行排序（用插入排序等稳定的算法)。 想一想：用哪种方法更快些？ 0

9 多关键字排序的实现方法通常有两种： • 最高位优先法MSD (Most Significant Digit first) 例：对一副扑克牌该如何排序？ 答：若规定花色为第一关键字（高位），面值为第二关键字 （低位），则使用MSD和LSD方法都可以达到排序目的。 MSD方法的思路：先设立4个花色“箱”，将全部牌按花色分 别归入4个箱内（每个箱中有13张牌）；然后对每个箱中的牌 按面值进行插入排序（或其它稳定算法）。 LSD方法的思路：先按面值分成13堆（每堆4张牌），然后对 每堆中的牌按花色进行排序（用插入排序等稳定的算法）。 想一想：用哪种方法更快些？ • 最低位优先法LSD (Least Significant Digit first)

2.单逻辑关键字怎样“按位值”排序？ 思路：设n个记录的序列为：(%，Y,V1),可以把每个 记录V的单关键码K火，看成是一个元组（， K),则其中的海一个分量KM(1≤j≤d)也可看成是 一个关键字。 注1：好=最高位，K=最低位；K共有d位，可看诚d元组， 注2：每个分量K灯(1≤j≤d)有radi种取值，则称radix为基数。 例1：关键码984可以看成是3元组：基数rad心为10 (9,8,4) (0,1,9) 例2：关键码dian可以看成是4元组；基数radix为26。 (d,i,a,n （ab,z) 10

10 2. 单逻辑关键字怎样“按位值”排序？ 设n 个记录的序列为：{V0 , V1 , ., Vn-1 }，可以把每个 记录Vi 的单关键码 Ki看成是一个d元组（Ki 1 , Ki 2 , ., Ki d），则其中的每一个分量Ki j ( 1 j  d ) 也可看成是 一个关键字。 4 注1： Ki 1＝最高位，Ki d＝最低位；Ki共有d位，可看成d元组； 注2： 每个分量Ki j (1  j  d ) 有radix种取值，则称radix为基数。 26 (9, 8, 4) (0, 1, ., 9) (d, i, a, n) （a, b, ., z） 例1：关键码984可以看成是 3 元组；基数radix 为 10 。 例2：关键码dian可以看成是 元组；基数radix 为 。 思路：